5. Обратная матрица

Обра́тная ма́трица — такая матрица A−1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.

Свойства обратной матрицы:

, где det обозначает определитель

для любых двух обратимых матриц A и B.

где * T обозначает транспонированную матрицу.

для любого коэффициента

Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A − 1 существует, то x = A − 1b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

Пример решения: http://www.mathelp.spb.ru/book1/omatrix.htm

6. Решение систем матричных уравнений линейным способом.

Запишем систему линейных 3 уравнений с 3 неизвестными

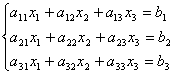
Составим матрицу из коэффициентов при неизвестных

А =

Введем в рассмотрение матрицы - столбцы для неизвестных и свободных членов:

Х = ; В =

Тогда систему (2) можно переписать в матричной форме

АХ=В

Умножив это уравнение на слева, получим , откуда = или

Следовательно, матрица - решение Х находится как произведение на В.

7. Метод Гаусса

Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.

Решить систему уравнений методом Гаусса:

x + y - 3z = 2,

3x - 2y + z = - 1,

2x + y - 2z = 0.

Решение. Выпишем расширенную матрицу данной системы:

и произведем следующие элементарные преобразования над ее строками:

а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:

~

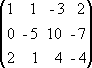
б) третью строку умножим на (-5) и прибавим к ней вторую:

В результате всех этих преобразований данная система приводится к треугольному виду:

x + y - 3z = 2,

-5y + 10z = -7,

- 10z = 13.

Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим x = - 0,7.

8. Векторы и линейные операции над ними

Вектор - направленный отрезок, то есть отрезок, у которого указаны начало и конец.

Суммой двух векторов и называется вектор, который идет из начала вектора в конец вектора при условии, что вектор приложен к концу вектора (правильно треугольника). Построение суммы изображено на рис. 1.

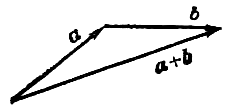
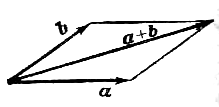
Наряду с правилом треугольника часто пользуются (равносильным ему) правилом параллелограма: если векторы и приведены к общему началу и на них построен параллелограмм, то сумма есть вектор, совпадающий с диагональю этого паралеллограмма, идущей из общего начала и Отсюда сразу следует, что

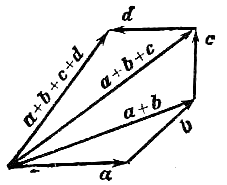
Сложение многих векторов производится при помощи последовательного применения правила треугольника (см. рис. 3, где изображено построение суммы четырех векторов , , , ).

Разность двух векторов и называется вектор, который в сумме с вектором составляет вектор . Если два вектора и приведены к общему началу, то разность их есть вектор, идущий из конца («вычитаемого») к концу «уменьшаемого»). Два вектора равной длины, лежащие на одной прямой и направленные в противоположные стороны, называются взаимно обратными: если один из них обозначен символом , то другой обозначается символом . Легко видеть, что . Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемого».

Произведение (или также ) вектора на число называется вектор, модуль которого равен произведению модуля вектора на модуль числа ; он параллелен вектору или лежит с ним на одной прямой и направлен так же, как вектор , если - число положительное, и противоположно вектору , если - число отрицательное.

Сложение векторов и умножение вектора на число называются линейными операциями над векторами.