14. Монотонные функции
Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.
Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Определения
Пусть
дана функция 
Тогда
функция f называется возраста́ющей на M, если
.
функция f называется стро́го возраста́ющей на M, если
.
функция f называется убыва́ющей на M, если
.
функция f называется стро́го убыва́ющей на M, если
.
(Строго) возрастающая или убывающая функция называется (строго) монотонной.
Другая терминология
Иногда возрастающие функции называют неубыва́ющими, а убывающие функции невозраста́ющими. Строго возрастающие функции тогда зовут просто возрастающими, а строго убывающие просто убывающими.
Свойства монотонных функций
Монотонная функция, определённая на интервале, измерима относительно борелевских сигма-алгебр.
Монотонная функция,
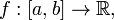определённая
на замкнутом интервале, ограничена.
В частности, она интегрируема
по Лебегу.Монотонная функция может иметь разрывы только первого рода. В частности, множество точек разрыва не более чем счётно.
Монотонная функция
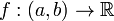дифференцируема почти
всюду относительно меры
Лебега.
Условия монотонности функции
(Критерий монотонности функции, имеющей производную на интервале) Пусть функция
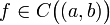непрерывна
на (a,b), и
имеет в каждой точке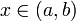 
производную f'(x). Тогда
f возрастает
на (a,b) тогда
и только тогда, когда 
f убывает
на (a,b) тогда
и только тогда, когда 
(Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция непрерывна на (a,b), и имеет в каждой точке производную f'(x). Тогда
если 
то f строго
возрастает на (a,b);
если 
то f строго
убывает на (a,b).
Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале (a,b). Точнее имеет место
(Критерий строгой монотонности функции, имеющей производную на интервале) Пусть
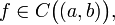и
всюду на интервале определена
производная f'(x). Тогда fстрого
возрастает на интервале (a,b) тогда
и только тогда, когда выполнены следующие
два условия:
Аналогично, f строго убывает на интервале (a,b) тогда и только тогда, когда выполнены следующие два условия:
"Условия монотонности функции (Критерий монотонности функции, имеющей производную на интервале): Пусть функция непрерывна на (a,b), и имеет в каждой точке производную f'(x). Тогда - f НЕ УБЫВАЕТ на (a,b) тогда и только тогда, когда ...далее по тексту f НЕ ВОЗРАСТАЕТ на (a,b) тогда и только тогда, когда ...далее по тексту"
15. Графы. Представления графов. Пути в графах
Граф — это совокупность непустого множества вершин и множества пар вершин.
Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — гиперссылки (см. Тематическая карта).
Представления графов. Список ребер
На этом шаге мы познакомимся с первым способом представления графов - списком ребер.
Знакомство со способами представления и обработки графов весьма поучительно. С одной стороны, графы являются достаточно наглядными объектами. С другой стороны, машинное представление графов допускает большое разнообразие. Сложность получения ответа на тот или иной вопрос относительно данного графа зависит, естественно, от способа представления графа. Поэтому в алгоритмах на графах взаимосвязь "алгоритм + структура данных" проявляется очень сильно. Один и тот же алгоритм, реализованный на различных структурах данных, очень часто приводит к совершенно разным программам.
Во многих задачах на графах выбор представления является решающим для повышения эффективности алгоритма. С другой стороны, переход от одного представления к другому относительно прост и может быть выполнен за O(|V|2) операций [1, с.355]. Поэтому если решение задачи на графе обязательно требует числа операций, по крайней мере пропорционального |V|2, то время ее решения не зависит от способа представления графа, так как оно может быть изменено за O(|V|2) операций.
Более экономным в отношении памяти (особенно в случае так называемых неплотных графов, когда |E| гораздо меньше |V|2) по сравнению с матрицей смежностей является метод представления графа с помощью структуры смежности, которая является в простейшем случае списком пар, соответствующих его ребрам [1, с.354].
Пара <x,y>, входящая в список ребер, соответствует ребру {x,y} в случае неориентированного графа и дуге (x,y), если граф ориентированный.
Например, приведем списки ребер, соответствующие неориентированным графам:
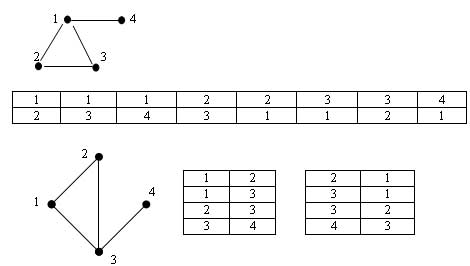Рис.1.
Примеры графов и списков ребер
Очевидно, что требуемый объем памяти в этом случае составляет 2|E|. Неудобством является большое число шагов (порядка |E| в худшем случае), необходимое для получения множества вершин, смежных данной вершине. Ясно, что при представлении графа в виде списка ребер, информация о вершинах может оказаться труднодоступной. Так будет в случае, когда число ребер намного больше числа вершин. Ситуацию можно значительно улучшить, если упорядочить множество пар лексикографически и применять при поиске нужного ребра (дуги) двоичный поиск, но лучшим решением во многих случаях оказывается структура данных, которая называется списками смежности.