Уравнения и свойства многополюсников

П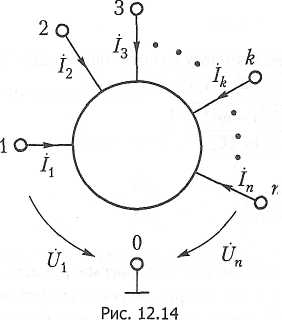 ри описании электрической цепи ее иногда пред­ставляют как совокупность фрагментов более общего вида (чем четырех- и двухполюсники), имеющих произвольное число внешних зажимов (полюсов), через которые такой фрагмент — мно­гополюсник — соединяется с другими участками цепи (рис. ).

Описание многополюсника как элемента цепи выражает связи между токами полюсов I_k и на­пряжениями входных узлов U_k относительно опорного узла цепи 0.

В общем виде такая связь для линейного многополюсника может быть вы­ражена в матричной форме:

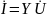
где 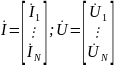- векторы токов и напряжений полюсов;

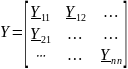- неопределенная матрица проводимостей многополюсника, квадратная матрица размера nп.

Матрица Y называется неопределенной, поскольку ее элементы Y_jk не являются независимыми друг от друга, так как токи полюсов, образующих сечение цепи, связаны друг с другом первым законом Кирхгофа и, следовательно, отдельные уравнения системы являются линейно зависимыми.

Поэтому неопределенная матрица проводимостей многополюсника является вырожденной — ее определи­тель равен нулю.

Н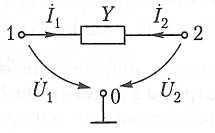 апример, описание двухполюсника с помощью неопределенной матрицы про­водимостей Y (рис. ) выражается двумя уравнениями:

I₁ =(U₁  U₂)Y; I₂ =(U₁ +U₂)Y,

или в матричной форме:

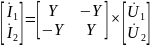
Отсюда видно, что всю существенную информацию о двухполюснике несет лишь один выделенный элемент неопределенной матрицы Y₁₁= Y. Недиагональ­ные элементы неопределенной матрицы проводимостей пассивного многопо­люсника Y_mk с одинаковыми индексами на основании принципа взаимности рав­ны друг другу: Y_mk= Y_km.

Для трехполюсных элементов цепи — трехполюсников (рис. ), к которым относятся, например, транзисторы, система уравнений для токов имеет вид:

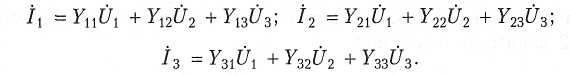
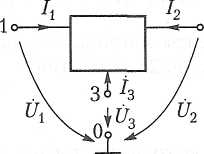
По первому закону Кирхгофа в этом случае имеем

Так как это равенство выполняется при любых значениях U₁, U₂ и U₃, то суммы проводимостей Y_km в каждой скобке должны быть равны нулю. Поэтому сумма элементов каждого столбца неопределенной матрицы проводимостей любого многополюсника — это справедливо не только для трехполюсника — равна нулю.

С другой стороны, если все входы многополюсника находятся под одинаковым потенциалом , то токи через все выходные зажимы не протекают Поэтому и сумма элементов каждой строки неопределенной матрицы проводимостей многополюсника также равна нулю.

Эти свойства позволяют записать неопределенную матрицу проводимостей трех­полюсника в следующей форме:

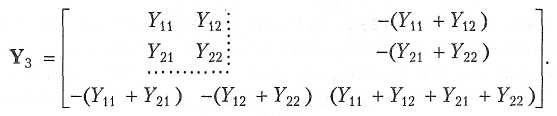
Таким образом, вся существенная информация о трехполюснике содержится лишь в выделенной клетке матрицы с элементами Y₁₁, Y₁₂, Y₂₁, Y₂₂. Эта клетка со­ответствует описанию трехполюсника как четырехполюсника, у которого за­жим 3 является общим для входной и выходной пар полюсов.

Такие четырех­полюсники с общим зажимом встречаются весьма часто, и, следовательно, вся рассмотренная выше теория четырехполюсников распространяется и на трехполюсники с общим зажимом для входной и выходной цепей.

11