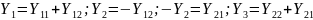Раздел Четырехполюсники и электрические фильтры.

Часть 1. Четырехполюсники. Основы теории четырехполюсников и

ЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ

1. Пассивные четырехполюсники.

2. Основные уравнения четырехполюсника.

3. П- и Т-образные схемы замещения четырехполюсника.

4. Соединения четырехполюсников.

Во многих случаях в силу сложности реальных электрических сетей и систем, их расчет при помощи рассмотренных выше методов затруднителен. Поэтому их разбивают на части с тем, чтобы анализируя каждую часть в отдельности упростить расчет всей системы в целом, и получить, в конечном счете, готовый ответ для всей системы.

Каждую составную часть системы называют многополюсником, характеризующегося уравнениями связи между его входными и выходными электрическими величинами ( обычно U, I ). При этом для исследования электрических цепей используют двух-, трех- и четырехполюсники.

Наибольшее распространение получили четырехполюсники, так как с помощью них моделируются как отдельные элементы, так и электрические системы в целом : ЛЭП, трансформаторы, фильтры, электронные устройства и т.д.

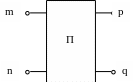Четырехполюсником называют электрическую схему, имеющую два входных и два выходных зажима. На схемах представляется в виде рис.1.

Если в четырехполюснике есть источники электрической энергии, то он активный (А), если нет – пассивный (П).

К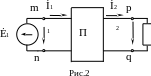 входным зажимам (m, n) обычно подсоединяются источники энергии, к выходным (p, q) – нагрузка. Все электрические величины отнесенные к входным зажимам снабжаются индексом 1 , а к выходным – индексом 2.

При выбранных направлениях входных и выходных напряжений и токов четырехполюсник является промежуточным звеном при передачи энергии от источника к нагрузке, которая включается между зажимами 2 и 2.

Выведем уравнения, связывающие между собой входные и выходные токи и напряжения пассивного четырехполюсника, воспользовавшись методом контурных токов. За I-контур примем контур, содержащий источник Е₁ с напряжением U₁ и током I₁, а второй контур – цепь с нагрузкой, характеризующуюся напряжением U₂ и током I₂.

Согласно методу контурных токов, правая часть первого уравнения = +U₁, а во втором контуре правая часть = -U₂, поскольку ток всегда протекает через нагрузку (рис.3). Решение двухконтурной цепи определяется системой уравнений:

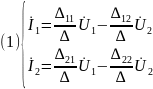
Отношения 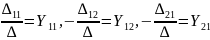, 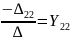… - имеют размерность проводимости с соответствующими индексами. Поскольку для линейного четырехполюсника ₁₂=₂₁, имеем Y₁₂= Y_21, в результате подстановки которых в систему (1) получаем уравнение четырехполюсника в Y-форме:

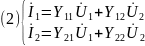
Из системы уравнений (2) выразим входное и выходное напряжение четырехполюсника

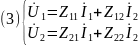
Получаем уравнение четырехполюсника через Z параметры (Z- форма), где

, , ,

.

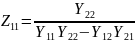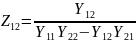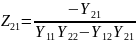
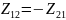Полученные соотношения (2) и (3) могут быть представлены в матричной или символической формах записи, т.е.

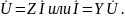
В матричной форме

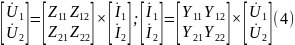
Матрицы Z и Y называют, матрицей холостого хода и короткого замыкания, соответственно.

При рассмотрении четырехполюсника как звена цепи передачи сигнала используют форму уравнений через А-параметры (А-форма). Данная форма позволяет выразить входные величины напряжения U₁ и тока I₁ через выходные параметры четырехполюсника U₂ и I₂.

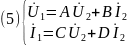
Здесь коэффициенты

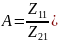
В матричной форме записи:

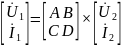, для которой выполняется условие AD – BC = 1.

Д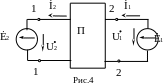 ля доказательства симметричности четырехполюсника достаточно поменять местами его вход и выход, учитывая направление токов (рис.4), тогда получим:

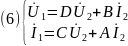
Следовательно, при равенстве A=D, поведение четырехполюсника аналогично как со стороны зажимов 1-1, так и 2-2 и такой четырехполюсник называется симметричным. Данный вывод позволяет выделить три независимых параметра четырехполюсника

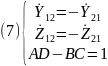
Таким образом, схемы замещения четырехполюсника должны иметь три связанных параметра минимум, из которых можно реализовать Т- и П-образные схемы замещения.

Р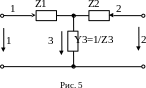 ассмотрим Т-образную схему рис.5. Для входного и выходного напряжений имеем:

.

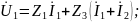
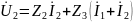Сопоставляя эти уравнения с Z-формой параметров четырехполюсника (3) получим условия их эквивалентности:

Z₁+Z₃ = Z₁₁  Z₁= Z₁₁ Z₃;

Z₂+Z₃ = Z₂₂  Z₂= Z₂₂ Z₃;

Z₃ = Z₁₂ =Z₂₁ .

П-образная схема замещения. Аналогично параметры для П-образной схемы выразим по второму закону Кирхгофа, через Y-форму:

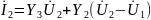
Сравним полученные выражения сравним с уравнениями четырехполюсника в Y- форме:

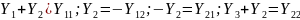
Откуда получаем выражения для П-образной схемы через Y-параметры