28. Равномерное распределение и его числовые характеристики.

Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке  , где  , если еёплотность   имеет вид:

где а и b параметры.

Интегрируя определённую выше плотность, получаем:

MX=(a+b)/2; DX=((b-a)^2)/12. Равномерное распределение используется в системах массового обслуживания, а так же при построении таблицы случайных чисел, используемых в прикладной статистике.

29. Показательное распределение.

Непрерывная величина Х имеет показательное распределение, если её функция плотности имеет вид:

где  параметр. Сл.Вел. используется в системах массового обслуживания. Смысл - число заявок обслуженных системой в ед. времени.

Ось х-асимптота.

Интегрируя плотность, получаем функцию показательного распределения:

Числовые характеристики: MX=1/; DX=1/(^2).

 30.Нормальное распределение.Св-ва фун-и плотности норм.распр. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности: . Нормальный закон распределения также называется законом Гаусса. Можно легко показать, что параметры   и  , входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х. Найдем функцию распределения F(x): График плотности нормального распределения называется нормальной кривой(кривой Гаусса).

График называется кривой нормального распределения. Если: a=0;=1, то сл. Вел. Называется нормарованной. : Свойства:

1. (-∞;+∞), f(x)>0

2. X<=0, fmax=f(a)=1/(*(2))

3. X1,2=a+-, fпер=f(x1,2)= 1/(*(2e))

4. Y=0 асимптота

5. f(x)dx=1.

31.Влияние параметров «» и «» на форму кривой нормального распределения.

1. Влияние а:

При изменении параметра а пик кривой сдвигается вдоль оси Ох с сохранением формы. Если а увеличивается. То пик сдвигается вправо. Если уменьшается, то влево. 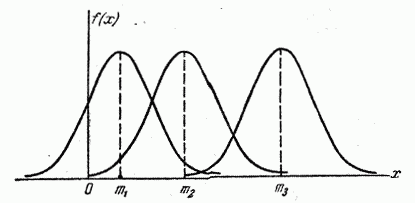а2>a1

2. Влияние : При изменении параметра  кривая деформируется: Если сигма уменьшается, то пик кривой вытягивается вдоль оси Оу, становится более островершинной.Если увеличивается, то приближается к оси Ох, становится более плосковершинной. Но как бы не деформировалась кривая, площадь под неё всегда равна 1 ед^2.

32.Вероятностный смысл параметров нормального распределения. Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается следующей плотностью вероятностей:

.Нормальное распределение определяется двумя параметрами: а и . Достаточно знать эти параметры, чтобы задать нормальное распределение. Вероятностный смысл этих параметров таков: а- есть математическое ожидание;  — среднее квадратическое отклонение нормального распределения.

Теорема: a=MX; =x. а это мат.ожидание нормальной случайной величины, а  её среднее квадратическое отклонение. Доказательство а=МХ:

Введем новую переменную

Тогда 

Первый интеграл равен нулю, так как под знаком интеграла стоит нечетная функция, а пределы интегрирования симметричны. Второй интеграл известен как интеграл Пуассона  .

 Поэтому M(x)=а