
- •Приложения производных
- •Задачи для самостоятельного решения
- •1.24. Уравнение касательной . Уравнение нормали . Графическая иллюстрация (рис.18).
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Формула Тейлора
- •Задачи для самостоятельного решения
- •Исследование функций и построение графиков
- •Задачи для самостоятельного решения
Приложения производных
Уравнения касательной и нормали к графику функции
Уравнение
касательной к графику функции
![]() в точке
в точке
![]() имеет вид:
имеет вид:
![]()
Уравнение нормали:
![]()
Рассмотрим
задание: написать уравнения касательной
и нормали к графику функции
в данной точке
![]() дать графическую иллюстрацию.
дать графическую иллюстрацию.
Приведем решения примеров.
Пример
1.38.
![]()
Решение.
![]()
![]()
Уравнение
касательной:
![]()
Уравнение
нормали:
![]() или
или
![]()
![]() окончательно
окончательно
![]()
П

Пример
1.39.
![]()
Решение.
![]()
![]()
![]()
Уравнение
касательной:
![]()
Уравнение
нормали:
![]() или
или
![]() ,
,
![]() окончательно
окончательно
![]() Приведем график (рис.16).
Приведем график (рис.16).

Задачи для самостоятельного решения
Написать уравнения касательной и нормали к графику функции в данной точке дать графическую иллюстрацию.
1.23. ![]()
1.24. ![]()
Ответы
1.23.
Уравнение
касательной
![]() .
Уравнение нормали
.
Уравнение нормали
![]() .
Графическая иллюстрация (рис.17).
.
Графическая иллюстрация (рис.17).
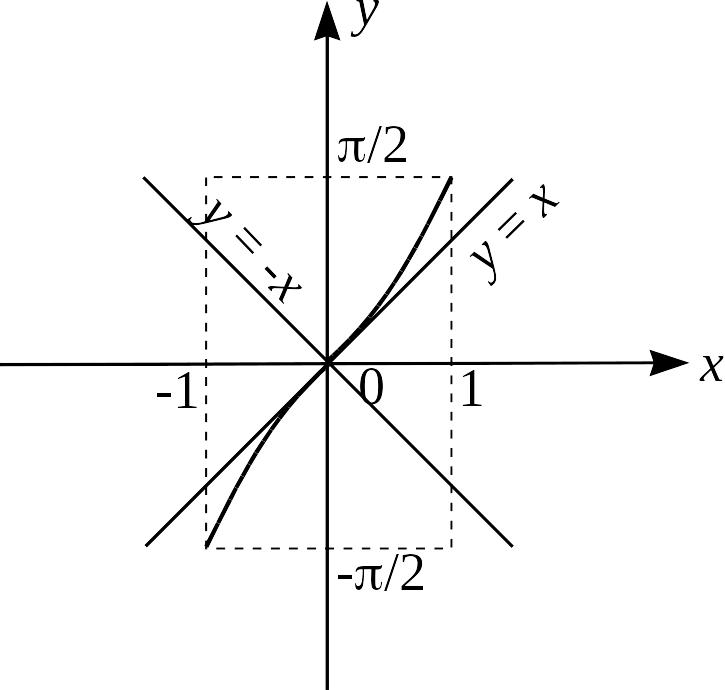
Рис.17.
1.24. Уравнение касательной . Уравнение нормали . Графическая иллюстрация (рис.18).
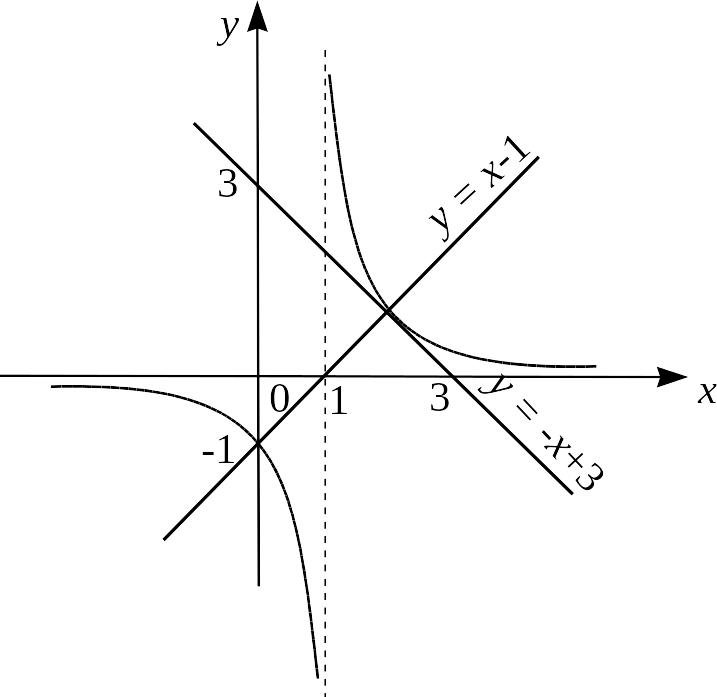
Рис.18.
Первый дифференциал и его применение для приближенных вычислений. Свойства первого дифференциала. Второй дифференциал
Приращение
дифференцируемой функции
![]()
![]() в точке
в точке
![]() может быть представлено в виде
может быть представлено в виде
![]() где величина
где величина
![]() такова, что
такова, что![]() при
при
![]() .
Выражение
.
Выражение
![]() называется главной линейной частью
приращения функции или первым
дифференциалом и обозначается
называется главной линейной частью
приращения функции или первым
дифференциалом и обозначается
![]() т.е.
т.е.
![]() Тогда приращение функции
записывается в виде
Тогда приращение функции
записывается в виде
![]() Если
Если
![]() мало, то можно считать, что
мало, то можно считать, что
![]()
![]() Перенеся
Перенеся
![]() в правую часть последнего выражения,
мы получим формулу для приближенного
вычисления значений функции
в точке
в правую часть последнего выражения,
мы получим формулу для приближенного
вычисления значений функции
в точке
![]() :
:
![]()
Приведем свойства первого дифференциала:
1)
![]() ;
;
2)
![]() ;
;
3)
 .
.
Второй
дифференциал функции
![]() имеет вид:
имеет вид:
![]() ,
где
,
где
![]() - вторая производная функции
.
- вторая производная функции
.
Рассмотрим задание: вычислить значение функции, используя формулу приближенных вычислений.
Пример
1.40.
Вычислить приближенно
![]()
Решение.
В качестве точки
естественно взять
![]() тогда
тогда
![]() и
и
![]() В качестве используемой функции возьмем
В качестве используемой функции возьмем
![]() Тогда
Тогда
![]()
![]()
![]() По формуле приближенных вычислений
получим:
По формуле приближенных вычислений
получим:
![]()
Пример
1.41.
Вычислить приближенно
![]()
Решение.
Используем функцию
![]() точка
точка
![]()
![]() тогда
тогда
![]()
![]()
![]()
![]() По формуле приближенных вычислений
получим:
По формуле приближенных вычислений
получим:
![]()
Задачи для самостоятельного решения
Вычислить значение функции, используя формулу приближенных вычислений.
1.25. ![]()
1.26. ![]()
Ответы
1.25.
![]() .
.
1.26.
![]() .
.
Вычисление пределов функций с помощью правила Лопиталя
Правило Лопиталя значительно облегчает вычисление пределов, сводя вычисление предела отношения двух функций к вычислению предела отношения их производных. Правило Лопиталя формулируется в виде теоремы 1.
Теорема 1. Пусть
в некоторой окрестности V точки
функции
и
![]() дифференцируемы всюду, кроме, может
быть, самой точки
,
и пусть
дифференцируемы всюду, кроме, может
быть, самой точки
,
и пусть
![]() в V. Если функции
и
являются одновременно либо бесконечно
малыми, либо бесконечно большими при
в V. Если функции
и
являются одновременно либо бесконечно
малыми, либо бесконечно большими при
![]() и при этом существует предел отношения
и при этом существует предел отношения
![]() их производных при
,
то существует также и предел отношения
их производных при
,
то существует также и предел отношения
![]() самих функций, причем
самих функций, причем

Теорема применима
и при
![]()
При использовании
правила Лопиталя на практике следует
проверять условия его выполнения, в
частности, при многократном последовательном
применении правила необходимо
устанавливать на каждом шаге существование
предела отношения производных
соответствующего порядка при
![]()
Рассмотрим вычисление пределов функций с помощью правила Лопиталя. Приведем решения примеров.
Пример 1.42.
![]()
Решение.
Числитель и знаменатель являются
бесконечно малыми функциями при
![]() (имеем
неопределенность вида
(имеем
неопределенность вида
![]() ).
Условия теоремы 1 выполнены. Согласно
правилу Лопиталя
).
Условия теоремы 1 выполнены. Согласно
правилу Лопиталя

Числитель стремится
к нулю, а знаменатель - к единице, значит,
![]()
Пример 1.43.
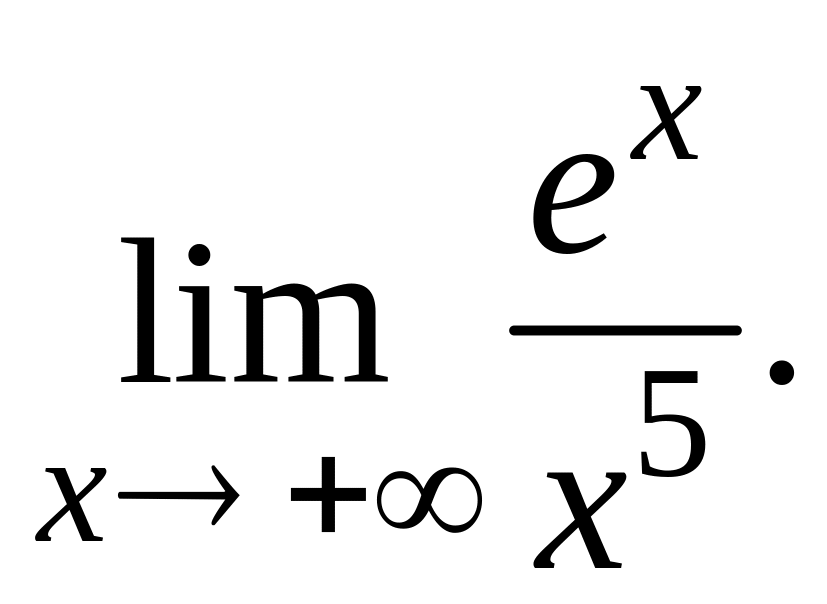
Решение.
Числитель и знаменатель стремятся к
бесконечности при
![]() (имеем неопределенность вида
(имеем неопределенность вида
![]() ).
Условия теоремы 1 выполнены. Согласно
правилу Лопиталя
).
Условия теоремы 1 выполнены. Согласно
правилу Лопиталя
 Условия теоремы 1 опять выполнены,
следовательно,
Условия теоремы 1 опять выполнены,
следовательно,

(на каждом шаге
проверяется существование предела
отношения производных). Последнее
выражение не является неопределенным,
а стремится к бесконечности. Окончательно
получим
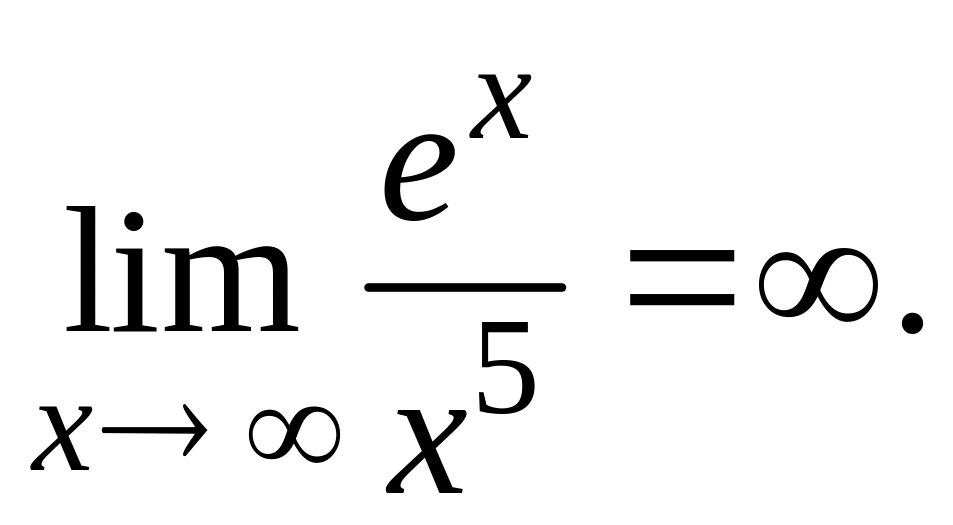
Приведем пример, когда правило Лопиталя не позволяет вычислить предел.
Пример 1.44.
![]()
Решение. Покажем, что конечный предел существует, и вычислим его, не применяя правило Лопиталя:

Применим правило
Лопиталя:
![]()
Последний предел не существует, но из этого не следует, что исходный предел не существует.
Правило Лопиталя
применимо и для вычисления предела
выражения
![]() ,
который представляет неопределенность
вида: а)
,
который представляет неопределенность
вида: а) ![]() ;
б)
;
б) ![]() ;
в)
;
в) ![]() .
В первом случае
- бесконечно малая функция, во втором
случае
-
бесконечно большая функция, в третьем
случае
- функция,
имеющая предел, равный единице. Функция
в первых двух случаях - бесконечно малая,
а третьем случае - бесконечно большая.
Для вычисления предела равенство
логарифмируется, получаем
.
В первом случае
- бесконечно малая функция, во втором
случае
-
бесконечно большая функция, в третьем
случае
- функция,
имеющая предел, равный единице. Функция
в первых двух случаях - бесконечно малая,
а третьем случае - бесконечно большая.
Для вычисления предела равенство
логарифмируется, получаем
![]() После этого находим предел
После этого находим предел
![]() ,
используя правило Лопиталя. Потенцируя,
находим и предел y.
,
используя правило Лопиталя. Потенцируя,
находим и предел y.
Пример 1.45.
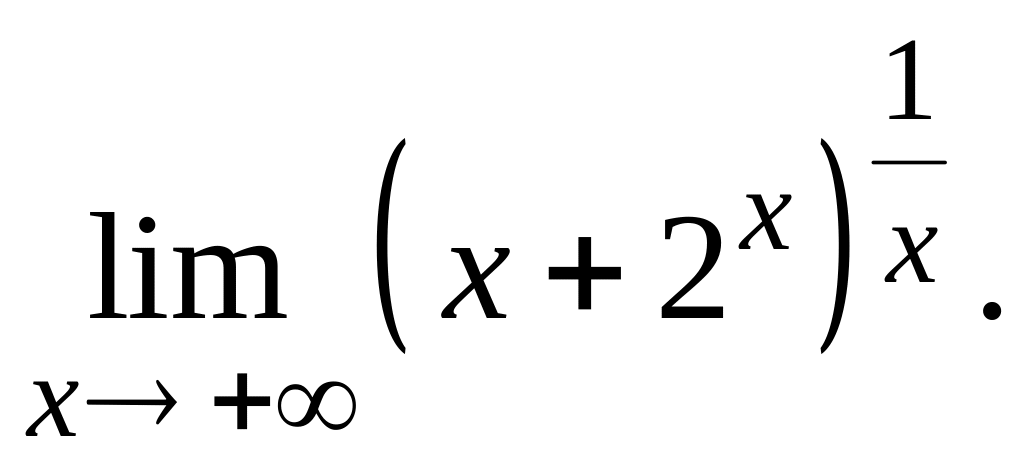
Решение.
Прологарифмируем выражение
 по основанию e, получим
по основанию e, получим
 Тогда
Тогда
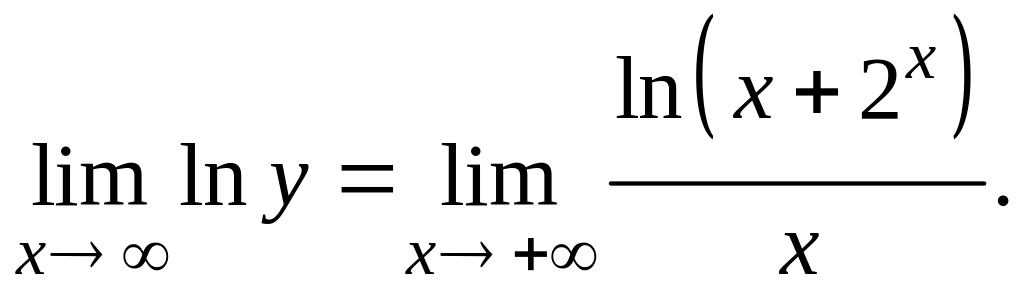
Условия теоремы 1 выполнены, поэтому применимо правило Лопиталя:

Итак,
![]() следовательно,
следовательно,

