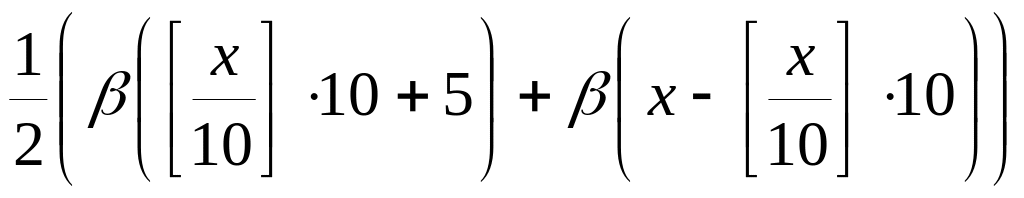Метод построения функций принадлежности на основе экспертных оценок.

Рассматривается метод построения функций принадлежности нечетких чисел, приблизительно равных некоторому четкому числу, и приближенных интервальных оценок. Задача сводится к отысканию параметров заранее заданной (экспоненциальной) функции, при решении которой используются результаты экспертного опроса.

Краткие сведения о методе. Рассмотрим особенности построения функций принадлежности для приближенных точечных (например, X ПРИБЛИЗИТЕЛЬНО РАВЕН 10) и интервальных оценок (вида X НАХОДИТСЯ ПРИБЛИЗИТЕЛЬНО В ИНТЕРВАЛЕ ОТ 8 ДО 11). На рис. 1 изображены функции принадлежности множеств, которые соответствуют этим оценкам. Естественно предположить, что функцию, представленную на рис. 1(б), необходимо строить следующим образом:

если , то ;

если , то ;

если , то ,

где — функция принадлежности нечеткому интервалу (α, β);

и — функции принадлежности нечетким множествам чисел, приближенно равных соответственно α и β. Они строятся аналогично функции, график которой приведен на рис. 1(а).

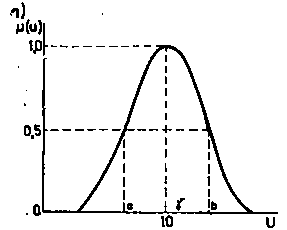
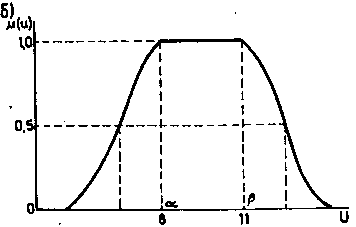
Рис. 1 Функции принадлежности нечетких множеств, соответствующих приближенной точечной оценке

При построении функции принадлежности чисел, приблизительно равных некоторому числу К, можно использовать функцию

, (1)

где α зависит от требуемой степени нечеткости и определяется из выражения

,

β — расстояние между точками перехода для , т.е. точками, в которых функция вида (1) принимает значение 0.5. На рис. 1(a) эти точки обозначены a и b.

Таким образом, задача построения для некоторого числа сводится к отысканию параметров a и b, чтобы затем можно было определить β(x), с помощью β(x) — α и, используя α, построить .

Для определения множества вида ЧИСЛО, ПРИБЛИЗИТЕЛЬНО РАВНОЕ К, следует выяснить, как эксперты представляют себе границы классов таких чисел. Для этого проводились статистические исследования. Опрашиваемым предлагали назвать такие a(К) и b(K), которые, по их мнению, отделяют числа, приблизительно равные заданному K, от чисел, таковыми не являющихся. Полученные результаты после некоторой обработки сведены в табл. 1. Рассмотрим натуральное число K. Пусть его младшая значащая цифра имеет порядок q. Разобьем возможные значения q на классы вычетов по модулю 3 и введем переменную d, значения которой будут являться представителями данных классов {0, 1, 2}. Получим классы эквивалентности: , .

Таблица 1 –

Расстояния между точками перехода

X	β(x)
1,2,3,4,6,7,8,9	0.46·x
10, 20, 30, 40, 60, 80, 90	(0.357–0.00163x)x
35, 45, 55, 65, 75, 85, 95	(0.213-0.00067x)x
5	2.8
15	6.48
25	6.75
50	24
Прочие двузначные числа

Введем целочисленную переменную X, изменяющуюся в пределах от 1 до 99, и будем считать, что для каждого ее значения известны параметры a(x) и b(x), а следовательно, и . На основании результатов опроса выяснилось, что значения в зависимости от X можно находить так, как показано в табл. 1 ([...] — целая часть числа). Значение зависит также от того, к какому классу М_d принадлежит число K.

Обозначим через r_q цифру, стоящую в q-м разряде числа K. Тогда:

1. При (например, 300, 300000, 5·10⁸ и т.д.) зависит только от младшей значащей цифры числа K, т.е. от r_q: ; , где находится из табл. 1.7.

2. При (например, 101, 202000, 5·10⁹ и т.д.) возможны два варианта:

а) r_q+1 = 0, тогда зависит только от r_q: х = r_q, ;

б) r_q+1 ≠ 0, тогда зависит от двух последних значащих цифр числа К: ; .

3. При (например, 2140, 20 и т.д.) также возможны два варианта:

а) r_q+1 = 0, тогда ;

б) r_q+1 ≠ 0, тогда ; .

После того как для числа K найдено значение , строим функцию принадлежности для , используя формулу (1).

С помощью указанного алгоритма могут быть также построены функции принадлежности в случае, когда K выражается десятичной дробью. При этом алгоритм применяется к мантиссе дроби, а затем учитывается ее порядок.

Примеры использования метода. Пример 1. Имеем приближенную точечную экспертную оценку X ПРИБЛИЗИТЕЛЬНО РАВЕН 235. Согласно вышеописанному алгоритму, К = 235. Далее определяем значение переменных q, r_q, r_q+1 и d. Младшая значащая цифра числа К стоит в разряде единиц, т.е. имеем q=1; r₁ = 5 — младшая значащая цифра числа K; r₂ = 3 — цифра, имеющая порядок на единицу выше порядка младшей значащей цифры.

При делении числа q на 3 в остатке получаем 1, т.е. число К принадлежит к классу эквивалентности М₁ и переменная d получает значение единицу. Следуя описанному методу, переходим к п. 2.б, так как r_q+1 = r₂ ≠ 0. Тогда выражение для переменной X: .

Определим интересующую нас величину , где находится из табл. 1.7. Так, для β(35) =(0,213-0,0006x)х; . Окончательно

.

Теперь, зная расстояние между точками перехода, можно построить функцию принадлежности нечеткого множества, соответствующую экспертной оценке X ПРИБЛИЗИТЕЛЬНО РАВЕН 235, по формуле

, .

Полученная функция принадлежности приведена на рис. 2, где а и b — точки перехода:

;

.

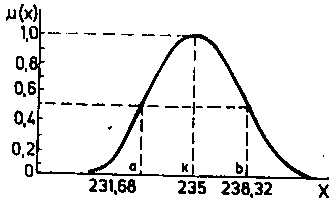
Рис. 2 Функция принадлежности нечеткого множества, соответствующего точечной оценке ПРИБЛИЗИТЕЛЬНО 235

Пример 2. Имеем оценку X НАХОДИТСЯ ПРИБЛИЗИТЕЛЬНО В ИНТЕРВАЛЕ ОТ 8 ДО 11. На этом интервале функция принадлежности равна единице, а за его пределами будет повторять функции принадлежности, соответствующие точечным оценкам X ПРИБЛИЗИТЕЛЬНО РАВЕН 8 и X ПРИБЛИЗИТЕЛЬНО РАВЕН 11 слева и справа от интервала. Для построения функции принадлежности нечеткого множества, соответствующего интервальной оценке, необходимо дважды воспользоваться описанным выше методом.

Имеем К=8. Находим q, r_q, r_q+1 и d; q=1,так как единственная значащая цифра стоит в разряде единиц; , , поскольку в разряде десятков значащих цифр нет. При делении q на 3 в остатке получаем 1, следовательно, d=1. В соответствии с методом переходим к п. 2.а. Выражение для нахождения переменной X: . Для величины имеем ; , где β(8) находится по табл. 1: .

Теперь определим расстояние между точками перехода для K=11. Находим значения переменных q, r_q, r_q+1 и d: младшая значащая цифра числа K стоит в разряде единиц, т.е. имеем q=1, ; — цифра, порядок которой на единицу выше порядка младшей значащей цифры K При делении числа q на 3 в остатке получаем 1, следовательно, число К принадлежит к классу эквивалентности М₁, переменная d получает значение единицу.

Так как , переходим к п. 2.б, где . Интересующая нас величина определяется в соответствии с выражением , где находится из табл. 1, т.е.

,

.

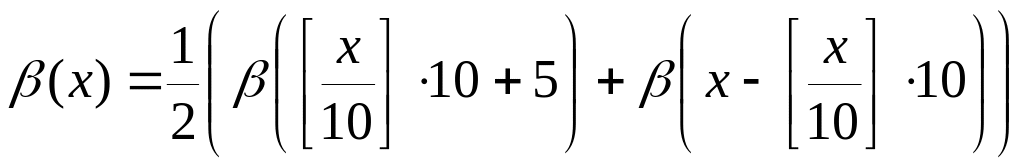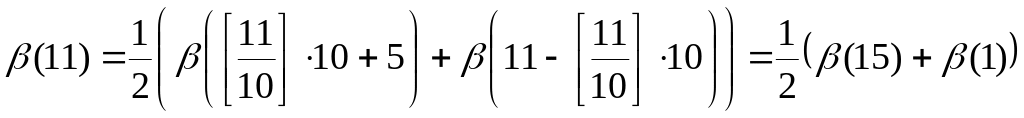Здесь ; найдены по табл. 1. Таким образом,

.

Для построения функции принадлежности нечеткого множества, соответствующего интервальной оценке, построим функции принадлежности нечетких множеств, соответствующих точечным оценкам с вершинами 8 и 11.

Функция принадлежности будет иметь вид, приведенный на рис. 3, где

;

• точки перехода.

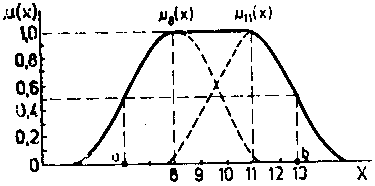
Рис. 3 Функция принадлежности нечеткого множества, соответствующего интервальной оценке ПРИБЛИЗИТЕЛЬНО В ИНТЕРВАЛЕ ОТ 8 ДО 11

Обратите особое внимание, что в теоретических основах метода присутствуют ошибки (в таблице 1 ошибок нет). Необходимо исправить ошибки и провести расчеты.

Дополнительная информация к заданию №8