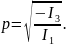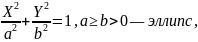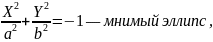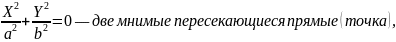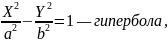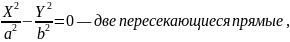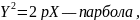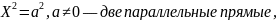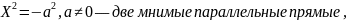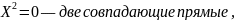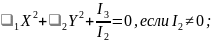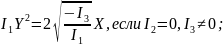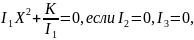Кривые второго порядка
Пусть
кивая Г задана в декартовой прямоугольной
системе координат
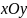 уравнением
уравнением
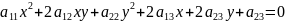
Если
хотя бы один из коэффициентов
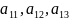 отличен от нуля, то кривую Г называют
кривой
второго порядка.
отличен от нуля, то кривую Г называют
кривой
второго порядка.
Теорема
1. Для
произвольной кривой порядка Г существует
такая декартова прямоугольная система
координат
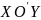 ,
что в этой системе кривая Г задана
уравнением одного из следующих
канонических
видов:
,
что в этой системе кривая Г задана
уравнением одного из следующих
канонических
видов:
В
этих уравнениях
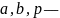 положительные параметры.
положительные параметры.
Систему координат назовем канонической системой координат, а систему координат — общей системой координат.
Функция
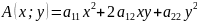 называется квадратичной
формой,
соответствующей уравнению
называется квадратичной
формой,
соответствующей уравнению
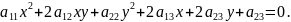
Характеристическим
уравнением
квадратичной формы
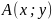 называется уравнение
называется уравнение
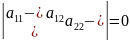
а
корни
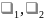 уравнения называют характеристическими
числами
квадратичной формы
уравнения называют характеристическими
числами
квадратичной формы
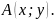
Характеристическое уравнение записывается в виде
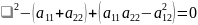
и имеет дискриминант
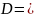 .
.
Всегда
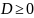 и характеристические числа квадратичной
формы
и характеристические числа квадратичной
формы
 находятся по формуле
находятся по формуле
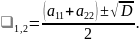
В
общем случае характеристическое
уравнение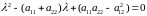 записывается в виде
записывается в виде
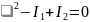
где
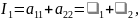
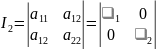
Обозначим
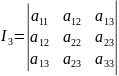
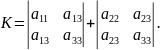
Значения
 не меняются при переходе от одной
декартовой прямоугольной системы
координат к другой, полученной в
результате поворота осей координат и
переноса начала координат, то есть
являются инвариантами
кривой Г относительно поворота осей
координат и переноса начала.
Значение K
является инвариантом
кривой Г только относительно поворота
осей координат.
не меняются при переходе от одной
декартовой прямоугольной системы
координат к другой, полученной в
результате поворота осей координат и
переноса начала координат, то есть
являются инвариантами
кривой Г относительно поворота осей
координат и переноса начала.
Значение K
является инвариантом
кривой Г только относительно поворота
осей координат.
Теорема 2.
Для
любой кривой второго порядка Г существуют
угол
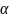 и числа
и числа
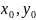 такие, что с помощью преобразования
поворота осей координат и переноса
начала координат
такие, что с помощью преобразования
поворота осей координат и переноса
начала координат
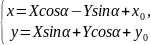
уравнение приводится к одному из следующих трех видов:
Где
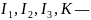 определены формулами, а
определены формулами, а
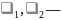 корни характеристического уравнения
корни характеристического уравнения
Замечание.
Для
эллипса
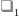 — меньший по абсолютной величине корень
характеристического уравнения, для
гиперболы
— корень характеристического уравнения,
знак которого совпадает со знаком
— меньший по абсолютной величине корень
характеристического уравнения, для
гиперболы
— корень характеристического уравнения,
знак которого совпадает со знаком
Классификация кривых второго порядка
В
зависимости от значения инварианта
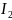 принята следующая классификация кривых
второго порядка:
принята следующая классификация кривых
второго порядка:
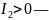 кривая
эллиптического
типа;
кривая
эллиптического
типа;
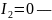 кривая
параболического
типа;
кривая
параболического
типа;
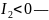 кривая
параболического типа.
кривая
параболического типа.
Кривая
второго порядка называется центральной,
если
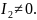
Кривые
эллиптического
и параболического
типа являются центральными
кривыми.
Центром кривой второго порядка Г
называется такая точка плоскости, по
отношению к которой точки этой кривой
расположены симметрично парами. Точка
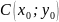 является центром кривой второго порядка,
определяемой уравнением
в том и только в том случае, когда ее
координаты удовлетворяют уравнениям
является центром кривой второго порядка,
определяемой уравнением
в том и только в том случае, когда ее
координаты удовлетворяют уравнениям
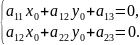
Если
линия — эллипс и
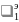 —
меньший
по абсолютной величине корень
характеристического уравнения, то
формула
—
меньший
по абсолютной величине корень
характеристического уравнения, то
формула
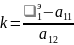
определяет угловой коэффициент большей оси эллипса.
Если
уравнение
определяет гиперболу и
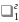 — корень характеристического уравнения,
знак которого совпадает со знаком
— корень характеристического уравнения,
знак которого совпадает со знаком
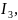 то формула
то формула
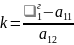
дает угловой коэффициент вещественной оси гиперболы.
Расположение параболы относительно начальной системы координат будет известно, если будут известны вершины параболы, вектор, направленный по ее оси в сторону вогнутости, и параметр.
Вершина параболы определяется при решении уравнения оси параболы
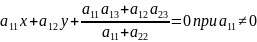
или
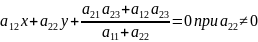
Совместно с уравнением параболы
Вектор
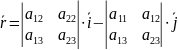
параллелен оси параболы и направлен в сторону ее вогнутости. Параметр параболы определяется по формуле: