3.Уравнение Шредингера, волновая функция, дополнительное условие, накладываемое на волновую функцию.

Как найти волновую функцию частицы, движущуюся в произвольном силовом поле с потенциальной энергией 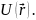Волновая функция в квантовой механике определяется из уравнения, впервые найденного Шредингером.

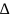-оператор Лапласа

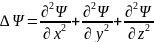
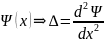
Волновая функция 𝛹 – ненаблюдаемая величина.

Для получения волновой функции для уравнения Шредингера на волновую функцию должны быть наложены следующие условия:

-одному начальному или двум граничным условиям координат

-однозначности

-непрерывности 𝛹,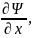

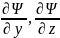
-условию нормировки

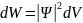
Вероятность нахождения в объеме 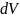равна

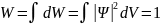- условие нормировки 𝛹

Мы найдем вероятность нахождения частиц в какой-нибудь точке пространства. Если частица существует, то это будет вероятность достоверного события, которая равна 100% или 1.

Совокупность этих условий позволяет найти единичное решение уравнения Шредингера – волновую функцию.

4.Классификация элементарных частиц.

За основу классификации выбираем массу покоя частицы. Все частицы делятся на три больших класса:

-лептоны (легкие частицы)

-мезоны (средние частицы)

-барионы (тяжелые частицы)

1)нуклоны

2)гипероны

-фотон

Кроме всех перечисленных в таблице частиц у всех существуют античастицы, которые обладают теми же характеристиками, но знак заряда противоположный. Существование античастиц было предсказано теоретически Дираком, который в 1920г. Вывел релятивистское волновое уравнение для электрона с учетом спина.

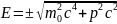
С современной точки зрения физически вакуум представляет собой – когда все отрицательные энергии заполнены, все положительнее – пустые; электрон себя никак не проявляет.

Нужно воспользоваться таблицей с лекции

Билет № 23.

1.Графическое представление колебаний, метод векторной диаграммы.

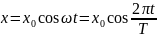
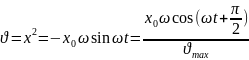
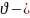гармонических колебаний, амплитуда скорости, отличается от амплитуды смещения в ω раз

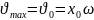, а по фазе скорость опережает смещение на 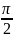или по времени на

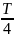
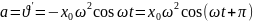
a – гармоническое колебание, амплитуда ускорения или максимальное ускорении отличающееся от амплитуды смещения на 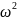раз, а по фазе опережает смещение на или колеблется в противофазе.

Метод векторной диаграммы используют, чтобы удобно и наглядно изображать гармоническое колебание. Выбирают т. О – полюс и проводится полярная ось. Каждому гармоническому колебанию ставится соответствующий вектор, длина которого равна амплитуде колебания, а данный вектор составляет угол с полярной осью.

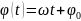–фаза колебания

С течением времени угол растет, следовательно вектор вращается вокруг т.О с const ω.

По гармоническому закону изменяется проекция на ось Особенно удобно изображается на векторной диаграмме когерентные колебания.

2.Понятие о волновом поле и волновом процессе, фронт волны, волновые поверхности.

Процесс распространения колебаний физической величины в пространстве называется волновым процессом, а одиночные колебания в пространстве называются одиночной волной или просто волной.

Область пространства, заполненная волнами, распространяющаяся от какого-либо источника называется волновым полем.

Необходимое условие существования волнового процесса является наличие связи между колебаниями какой-либо величины в разных точках пространства.

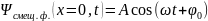
Точка с координатой х будет повторять это же движение, но запаздывая по времени на промежуток времени τ, необходимо чтобы волна распространялась от 0 до х с постоянной фазовой скоростью.

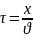
Фронт волны – волновая поверхность, самая удаленная в момент времени t от источника. Форма волновой поверхности подобна форме фронта волны.

Волновые поверхности:

От точечного источника распространения – сферические волны (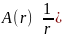

От линейного источника распространения – цилиндрические волны (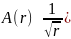

От плоского источника распространения – плоские (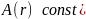

3.Корпускулярные и волновые свойства электромагнитного излучения. Эффект Коптлера. Фотоны.

Фотоны – кванты электромагнитного излучения

4.Распределение Больцмана молекул по потенциальным энергиям.

Как следует из основной молекулярной теории, получим:

Больцман предположил, что поде сил тяжести не является выделенным силовым полем и если газ находится в некотором силовом поле, так что его частица области потенциальной энергией, то число частиц обладает потенциальной энергией.

1)U→0 переходит в распространение Максвелла

2)проинтегрируем и левую, и правую часть переходит в распространение Больцмана

Билет № 24.

1.Кинематические характеристики гармонического осциллятора, смещение, скорость, ускорение.

Простым гармоническим колебанием называется процесс изменения физической величины x(t), описываемый уравнением x=x₀cos(ωt+ ₀)

Система совершает гармонические колебания, называемые гармоническим осциллятором

x=A*sin(ωt+ ₀), где ₀= -

Параметры гармонических колебаний:

-A,x₀-амплитуда гармонических колебаний определяет максимальное из возможных значений , значение x ,которое она принимает за время колебаний x_max=x₀*1 x₀>0

A-наибольшее отклонение системы от положения равновесия. Определяется начальными условиями.

-Фаза колебаний 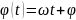₀

₀ –начальная фаза

ω-скорость изменения фазы

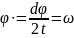- циклическая частота колебаний(рад/с)

x(t+T)=x(t)

x₀cos(ωt+wt+ ₀)=x₀cos(wt+ ₀)

ωT=2 ω=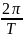 T=

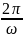
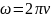ν=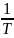

ν-число колебаний за 1 сек.

Смысл фазы

x=x₀cos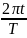 при ₀=0

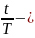часть периода

Фаза характеризует cостояние данного колебательного процесса, она показывает какая доля периода (в радианной мере) пройдено колеблющейся системой к данному моменту времени t и, следовательно показывает какое из состояний системы реализуется в данный момент. Начальная фаза ₀ совместно с амплитудой показывает, в каком состоянии находится колебательная система в момент времени t=0.Задавая начальные условия, находим амплитуду и начальную фазу.

гармонических колебаний, амплитуда скорости, отличается от амплитуды смещения в ω раз

, а по фазе скорость опережает смещение на или по времени на

a – гармоническое колебание, амплитуда ускорения или максимальное ускорении отличающееся от амплитуды смещения на раз, а по фазе опережает смещение на или колеблется в противофазе.

2.Уравнение бегущей монохроматической волны, амплитуда, частота, фаза волны, фазовая скорость.

Волновая функция 𝛹 может иметь различный фазовый смысл: давление, смещение

𝛹(r,t)=A(r)cos(ω(t-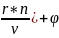 ₀)-для трехмерного пространства

n-единичный вектор в направлении распространения волны.

В произвольный момент времени t все пространства можно разделить на 2 области:

1.Область волнового поля

2.Область, куда волны еще не дошли из-за конечной скорости распространения волн. Граница между этими областями называется фронтами волны.

Амплитуда волны - амплитуда колебаний в данной точке волнового поля. Амплитуда волны зависит от r

( расстояние от оси)

А(r)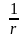 –сферическая волна

A(r)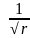 -цилиндрическая волна

A(r) const –плоская волна

Частота волны- -совпадает с частотой колебания источника волны.

Фаза волны - называется фаза колебаний в данной точке волнового поля в данный момент времени.

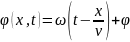₀

Существенное отличие волны от колебаний заключается в том что фаза колебаний зависит только от t , а волна колебаний распространяется в пространстве, потому фаза волны зависит от t,x

3.Квантовый гармонический осциллятор.

n=0,1 ,2 . . .

Классификация частиц может двигаться в таком потенциальном поле с любой энергией. Ее энергетический спектр непрерывен. Квантование частиц имеет дискретный энергетический спектр.

n – главное квантовое число

Спектр эквидестантный – расстояние между соседними уровнями одинаково и составляет hω₀.

поскольку разрешены переходы только между соседними уровнями в спектре излучения квантового осциллятора присутствует только частота ω₀.

Классификация частиц может покоиться на дне ямы. Квантованная частица имеет наименьшую энергию и называется энергией нулевых колебаний.

Если бы квантовая частица покоилась на дне ямы, мы могли бы одновременно точно указать координату точки где она покоится и ее импульс равный 0, что противоречит соотношению неопределенности.

Наличие нулевых колебаний было подтверждено экспериментально, при изучении рассеяния света на колебании атомов, при Т→0.

Если бы не было нулевых колебаний, то интенсивность рассеяния →0, а она стремится к какой-то конечной величине.

4.Частицы и античастицы в теории Дирака.

За основу классификации выбираем массу покоя частицы. Все частицы делятся на три больших класса:

-лептоны (легкие частицы)

-мезоны (средние частицы)

-барионы (тяжелые частицы)

1)нуклоны

2)гипероны

-фотон

Кроме всех перечисленных в таблице частиц у всех существуют античастицы, которые обладают теми же характеристиками, но знак заряда противоположный. Существование античастиц было предсказано теоретически Дираком, который в 1920г. Вывел релятивистское волновое уравнение для электрона с учетом спина.

С современной точки зрения физически вакуум представляет собой – когда все отрицательные энергии заполнены, все положительнее – пустые; электрон себя никак не проявляет

Билет № 25.

1. Гармонические колебания математического маятника.

Математический маятник - это материальная точка массой m на нити длинной l и находящейся в поле тяжести Земли.

Iα’’=ΣM

ml²α’’=-mgsinαL

α’’+(g/L)sinα=0

т.к. угол мал то α’’+(g/L)α=0; ω₀=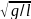

2. Расчет интерференции волнового поля в 2 х точечных когерентных источников

Согласно принципу суперпозиций сложение волн сводится к сложению колебаний в каждой точке пространства т.к. волны одинаково поляризованы- колеб. когерентны.

A_рез=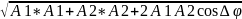

Ψ₁=A₁cos(ωt-k₁x₁+φ₀)

Ψ₂=A₂cos(ωt-k₂x₂+φ₀)

∆φ= ωt-k₁x₁+φ₀ – ωt+k₂x₂-φ₀=(2 /λ₀)(n₂x₂- n₁x₁)

∆_опт= n₂x₂- n₁x₁

∆_опт отличается от геометрической разности расстояний пройденных волнами учетом коэффициентов преломления.

∆_опт= n₂x₂- n₁x₁

∆_геом.= x₂- x₁

∆φ=(2 /λ₀)∆_опт.

3. Фермионы и бозоны принцип Паули.

Для классической частицы собственный момент импульса- любой микрочастицы тоже обладает собственным механическим моментом импульса не связанным с перемещением в пространстве. В квантовой механике этот момент называется спином(S).

Спин- квантовое свойство микрочастиц не имеющий аналогов в классичеcкой физике.

lL_sl=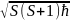 ; S- спиновое квантовое число.

L_sz=m_sћ ; S- целое => одна квантовая механики(бозоны)

S- полуцелое => другие квантовые механики(фермионы)

Принцип Паули:

В одной квантовой системе не может находиться больше 2-х или более фермионов, находящихся в одной и том же квантовом состоянии.

4. Ядро атома. Эмпирические свойства ядерных сил

Тяжелые элементарные частицы протоны и нейтроны находясь на близком расст.друг от друга < 10^-15 м взаимодейств.с помощью сильного ядерного взаимод.и образуют ядро. Ядро атома состоит только из протонов и нейтронов.

_ZX^A z-заряд ядра; А-масса ядра. Ядра с одинаковыми z-заряд ядра-изотопы.

Эмпирич.св-ва.

1)ядерные силы не зависят от электрич.заряда.

р-р

р-n

n-n

2) ядерные силы обладают св-вом насыщения

Каждый нуклон может взаимод-ть с огранич.числом нуклонов.

3)ядерные силы зависят от ориентации спинов частиц.