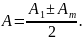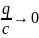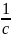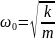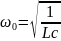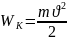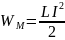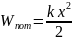3.Прохождени микрочастицы сквозь потенциальный барьер, туннельный эффект.

Потенциальный барьер – такое силовое поле, при котором в некоторой области пространства потенциальная энергия выше, чем в соседних областях, если на такой барьер падает классическая частица, у которой ε<U₀ то такая частица не сможет пройти этот барьер и оказаться в области справа от барьера. По этому Е = U₀ + E_кин , если E_кин<0

Для квантовой частицы: согласно соотношению неопределенности мы не можем одновременно абсолютно точно определить координату частицы и ее скорость. Поскольку кинетическая энергия – функция скорости, а потенциальная – координаты, представление полной энергии в виде суммы точно определенных частей кинетической и потенциальной энергии неправомерно.

Оценим вероятность такого перехода с помощью соотношения неопределенностей ∆х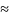 ћ/∆p= ћ/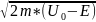 ∆х>d => ћ/ >или d=> (d/ћ)* <или 1

Wприближенно A*e^{-(2/ћ)*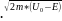 *d} Это условие выполняется тем легче, чем меньше масса частиц и чем меньше m и d.

Микрочастица может находится в областях пространства не доступно для классической частицы.

Рассмотрим явление автоэлектронной эммисии из металла (вырывание электронов из металлов под действием сильного электрического поля)

U=U₀-eE_x

На опыте установлено, что заметная автоэлектронная эмиссия начинается при полях сотни раз меньше, когда на границе еще существует конечный барьер и эмиссия связана с туннелированием электронов сквозь потенциальный барьер.

Так же автоэлектронная эмиссия наблюдается при автоэмиссии (явление в автоионизации электронов из отдельных атомов).

4.Виды фундаментальных функций элементарных частиц.

Способность к взаимному превращению, распадам и взаимодействию, является основным свойством элементарных частиц. Возможные реакции очень разнообразны и число их велико, но все они подчиняются нескольким законам сохранения, это известные нам законы сохранения энергии, с учетом энергии покоя ; импульса; момента импульса.

Закон сохранения барионного заряда

Если всем частицам бариона приписать барионное число B=+1 или анти В=-1, а остальным частицам В=0, то при любых превращениях в природе барионное число или барионный заряд сохраняются.

Билет № 9.

1. Основные параметры гармоническое колебание (график)

Простое гармоническое колебание – процесс изменения физической величины Х со временем t, описываемое уравнением x=x(0)cos(Wt+φ(0))

X(0)=A – амплитуда – определяет максимальное из возможных значений величины х, которое она принимает за время колебание . А - постоянное положительное значение, наибольшее отклонение системы от положения равновесия. Определяется начальными условиями.

Φ(t)=wt+ φ(0) – ваза колебаний φ(0)- начальная фаза, W-скорость изменения фазы

W= φ’=dφ/dt циклическая частота колебаний

X(t+T)=x(t); x(0)cos(wt+wT+ φ(0))=x(0)cos(wt+ φ(0))

wT=2 ;w=2 /T; w=2πν ; ν=1/T( гц) – количество колебаний системы а 1 секунду.

2.Дифракция Фраунгофера на решетке

d=a+b d-расстояние между двумя эквивалентными точками соседних щелей ,а- расстояние между щелями,в-ширина щели.диф.реш-диф. На одной щели с много лучевой интерференцией волн, проход. Через все щели (щели расположены строго периодически)∆=d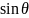 . ∆-разность лучей проходящих, через соседние щели. 𝜽=0-главный максимум нулевого порядка d =mλ m=±1,2,3,4,0. Условия главных max нулевого порядка гл.min b =mλ. Интенсивность всех главных макс. Возрастает в 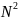раз по сравнению с диф. На одной щели. Картина диф. Тем больше выражена чем больше число из (N)в решетке.

3.Энергетически спектр и волновая функция микрочастицы в одномерной потенциальной яме.

энергетический спектр- набор разрешенных значений энергии, которые электроны могут иметь при движении в кристаллической решетке 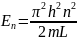. В потенциальной яме он становится дискретным(энергии частицы может принимать лишь отдельные значения) и считается квазинепроницаемым. Волновая функция: Ψ(F,t)=A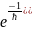 ,ћ-постоянная планка, Е-полная энергия в яме. Ψ(х)=А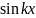 +B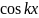 . A, B-произв.постоянные.

4.Квантовая статистика для бозонов. Функция распределение Бозе-Эйнштейна.

Если частица не подчиняется принципу Паули(бозоны- частицы с целочисленными значениями спина), то среднее число частиц, находящихся в состоянии 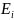: 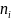= 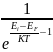.Для частиц,подчин,статистике Бозе Эйнштейна 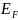<0 и значения n.Условия применения: Если 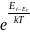>>1,то n=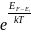 .Из условия транспортировки 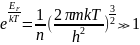.Кв. распределение:1)при больших m частиц.2)при высоких T.3)при малых ρ газа.

Билет № 10.

1. Гармонические колебания пружинного маятника.

Пружинный маятник совершает простое, поступательное движение .

F_тр=0 - скользит без трения.

ma=ԐF

mx”=-kx

x”+k/m*x=0 ; ⍵₀=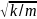

T=2 .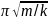

2. Частный случай прт:Кольца ньютона .

Установка для наблюдения колец Ньютона состоит из толстой плоско – параллельной стеклянной пластины, на которую помещёна плоская линза .Выпуклая стеклянная линза с большим радиусом кривизна.

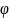= + =2

Роль тонкой плёнки играет воздушной зазор между линзой и пластиной.

Пусть на тонкую пластину называет перпендикулярно луч света

∆_oпm=2b+λ/2

=σ =2 /λ*∆; σ=λ/2

r-радиус кольца Ньютона

3.Соотношение неопределенности Гейзенберга.

Неопределённость – одновременное измерение сопряженных или дополнительных велечин удовлетворяющих условию:

∆x*∆p(x)≥ћ ∆y*∆p(y)≥ћ

∆z*∆p(z)≥ћ

∆x;∆y;∆z-неопределенные коэффициенты

∆p(x); ∆p(y); ∆p(z) –неопределённые значения соответствующих проекций импульса

∆E-неопределённое значение энергии

∆t≥ћ время нахождения частицы в соответствии с данной энергией

∆L(x)* ∆L(y) ≥ћ; ∆L(y)* ∆L(z) ≥ћ

Согласно соотнош.неопредел. Гейзенберга в квантовой механике не может существовать траектории и невозможно одновременно задать координаты и скорость

4. Атом водорода. Энергетический спектр.

– энергетический спектр

Если каким-либо способом электрону сообщить энергию меньшую чем 13,5эВ, то атом не ионизируется, а просто переходит на один из возбужденных уровней энергии.

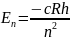для спектральных целей удобно энергию представлять в виде

R – постоянная Ридберга

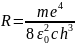
Рассмотрим переход электрона с энергетических уровней n’ на уровень n

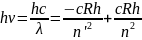
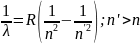
Билет № 11.

1. Гармонические колебания математического маятника.

Математический маятник-это материальная точка массой m на нити длиной l и находящейся в поле тяжести.

=

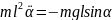
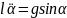
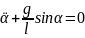
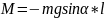
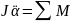
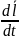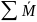
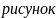
2. Дифракция волн. Принцип Гюйгенса - Френеля

Дифракция-это широкий круг явлений, описывающих влияние неоднородностей среды или помех на распространение волн.

Три утверждения Гюйгенса - Френеля:

Основаны на том, что все волновые поля равноправны и могут рассматриваться как самостоятельные источники вторичных сферических волн и отличаться лишь начальными фазами.

1)Положение фронта волны в момент времени t+△t можно получить, если рассматривать все точки волнового фронта в момент времени t, как самостоятельные точечные источники сферических волн и построить огибающую сферических волн.

2) Все вторичные источники когерентны между собой

3)Амплитуда волнового поля в процессе распространения волны получается как результат интерференции всех волновых источников.

3. Квантовые физические величины, квантовое число, пространственное квантование.

4. Атом водорода, оптический спектр излучения.

Если электрону сообщить энергии с 13.5 эВ, то атом не ионизируется переход на один из возбужденных уровней энергии.

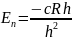
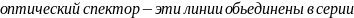
N=1-Лаймена

N=2- бальмера

N= 3- Пашена

Общее - один гл. квантовое число конеч уровней

Имеют одинаковую энергию, но отличаются орбитальным моментом импульса

Билет № 12.

1. Затухающие колебания в случае вязкого трения на примере пружинного маятника.

Жидкое или вязкое трение- трение между различ слоями жид. Или газов между ТВ. Телом и жидкостью при наличии смазки

Уравнение:

(рисунок)

Осн закон динамики поступ движ(2 закон Ньютона)

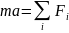
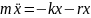
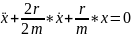
Убываеет по экспанициальному закону, быстрота затухания опред координт затухания

2. Уравнение стоячей волны. Амплитуда и фаза стоячей волны, узлы и пучности.

Важн частный случай интерференции наблюд при наложении 2-х встречных плоских волн с одинаковой амплитудой

Возникающий процесс назыв стоячей волной

Уравнение:

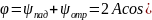)*cos(wt+ )

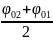Амплитуда постоянно у бегущ волны а у стоячей зависет от координаты х

Те точки где А=0 называются узлами стоячей волны

Те точки где А=мах-называются пучностями между соседними узлами

Фаза стоячей волны между 2 узлами постоянна

3. Квантово механические особенности движения микроцастицы в потенц. Яме.

L – ширина потенциальной ямы

Уравнение Шредингера для частицы, находящейся внутри ямы

На границе ямы на частицу действуют бесконечно большие силы. , которые не дают частице выйти наружу.

– энергетический спектр

4. Законы сохранения в физике элементарных частиц.

Закон сохранения очарования и прелести(charm и beauty)

Неизвестно следствием каких свойств симметрии является эти законы сохранения, а приводят к тому что некоторые частицы могут рождаться только парами или оказывают гораздо более долго живущими чем им полагается.

Билет № 13.

1.Аналогия механических и электромагнитных колебаний для электромагнитных волн.

пружина	емкость
F=-kx
m	L
x	q
	I
m	L
k
P=m	Ф=IL

2.Дифференциальное волновое уравнение для электромагнитных волн и его решение. Скорость электромагнитных волн.

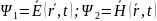
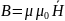
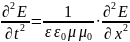
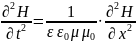
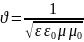
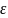– электрическая постоянная

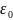– относительная диэлектрическая проницаемость среды

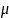- магнитная проницаемость

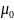- магнитная постоянная

3.Уравнение Шредингера для стационарных состояний

Стационарное состояние – состояние, в котором все наблюдаемые физические величины не зависят от времени.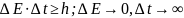

Все физические наблюдаемые величины в стационарном состоянии не зависят от времени, а 𝛹 (которая не является наблюдаемой величиной) зависит от времени по гармоническому закону:

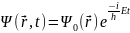
Если подставить 𝛹 в уравнение 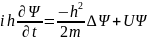мы получим уравнение Шредингера для стационарных состояний.

Δ – оператор Лапласа

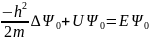
4.Оптический спектр атома водорода

Если каким-либо способом электрону сообщить энергию меньшую чем 13,5эВ, то атом не ионизируется, а просто переходит на один из возбужденных уровней энергии.

для спектральных целей удобно энергию представлять в виде

R – постоянная Ридберга

Рассмотрим переход электрона с энергетических уровней n’ на уровень n

Билет № 14.

1.Основные параметры затухающих колебаний, коэффициенты затухания, время релаксации, логарифмический декремент, добротность

Колебания при которых амплитуда и полная энергия гармонические колебания лишенного притока энергии из вне постепенно убывает с течением времени называются свободными затухающими колебаниями.

X”+2βx’W²(0)*x=0

X(t)=X(0)*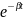 * cos(W(тильда)t + (0))

Β-коэффициент затухания, характерной скорости затухания колебаний

Β=r/2m; δ-логарифмический декремент затухания, δ=β*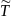 – величина обратная числу колебаний за время релаксации τ – время релаксации, время за которое амплитуда уменьшиться в е раз.

2. Интерференция света в тонкой плоско - параллельной пластине.

AD- фронт проходящих, CB-фронт отраженных

А(опт)=n(OA+OB)-OC+λ/2=2d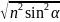 +1/2

2m*λ/2 – max; 2(m+1)*λ/2-min

(рисунок)

3. Соотношение неопределенностей Гейзенберга

Неопределённость – одновременное измерение сопряженных или дополнительных величин удовлетворяющих условию:

∆x*∆p(x)≥ћ ∆y*∆p(y)≥ћ

∆z*∆p(z)≥ћ

∆x;∆y;∆z-неопределенные коэффициенты

∆p(x); ∆p(y); ∆p(z) –неопределённые значения соответствующих проекций импульса

∆E-неопределённое значение энергии

∆t≥ћ время нахождения частицы в соответствии с данной энергией

∆L(x)* ∆L(y) ≥ћ; ∆L(y)* ∆L(z) ≥ћ

Согласно соотнош.неопредел. Гейзенберга в квантовой механике не может существовать траектории и невозможно одновременно задать координаты и скорость

4. – энергетический спектр

Если каким-либо способом электрону сообщить энергию меньшую чем 13,5эВ, то атом не ионизируется, а просто переходит на один из возбужденных уровней энергии.

для спектральных целей удобно энергию представлять в виде

R – постоянная Ридберга

Рассмотрим переход электрона с энергетических уровней n’ на уровень n

Билет № 15.

1.Гармонические колебания физического маятника

Физический маятник – твердое тело, свободно вращающееся вокруг горизонтальной оси, непроходящий через центр инерции тела.

L – расстояние от точки подвеса, через который проходит ось вращения.

Запишем основной закон динамики простого вращательного движения 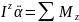, 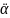- угловое ускорение ω.

I – момент инерции

М – момент силы

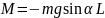
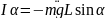
sinα≈α (ограничен малыми углами отклонений)

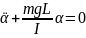
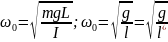
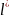- приведенная длина физического маятника.

Длина математического маятника, который имеет такой же период колебаний как и данный физический маятник

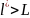
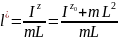
Используется для определения моментов инерции.

2.Условие наблюдения интерференции света. Оптическая разность хода волн. Условие максимума и минимума интерференции.

Главным условием является наличием двух когерентных точечных источников.

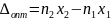
Условие максимума интерференции: если оптическая разность хода волн равна четному числу полуволн, то в данной точке наблюдается максимум интерференции.

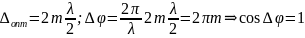
A=A₁+A₂, если А₁=А₂⇒А=2А₁, I=4I₁

Условие минимума интерференции: если оптическая разность хода волн равна нечетному числу полуволн, то в данной точке наблюдается минимум интерференции.

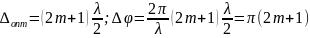
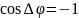
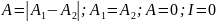
3.Волны де Бройля и их статическая интерференция

Французский ученый Луи де Бройль показал, что все опыты, в которых проявляется волновые свойства микрочастиц можно объяснить, если сопоставить движение микрочастиц и волновую функцию вида:

i – мнимая единица

Энергия и импульс связаны с ω,k

E= ћ ω

- длина волны де Бройля микрочастицы

4.Работа газа в изопроцессах

dA=Fdx=PSdx=pdV

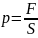
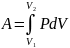
1)A=0 V=const

2)p=const

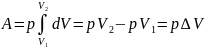
3)T=const

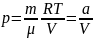
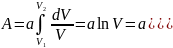
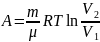
Билет № 16.

1. Дифференциальное уравнение гармонического колебания и его решение

Простым гармоническим колебанием называется процесс изменения физической величины x от t, описываемое уравнением x=x₀cos(ωt+φ)

Параметры:x₀,ω,φ₀- зависит от начальных условий

X^’’ +ω²x=0- дифф. уравнение гармонических колебаний

X=x₀cos(ω₀t+φ₀)- решение

2. Эффект Доплера для упругих волн

Изменения частоты волны при движении источника или приемника волн называется эффектом Доплера

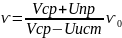
V_пр>0 приемник к источнику

V_пр<0 приемник от источника

V_ист>0 источник к приемнику

V_ист<0 источник от приемника

Скорость источника и приемника считаем положительной, когда расстояние между ними сокращается

3. Квантово механические особенности движения микрочастицы в одномерной бесконечно глубокой яме

В классической механике частицы, движущиеся в такой яме может, с равной вероятностью находится в любой точке внутри ямы квантовой, вероятность обнаружить частицу в различных точках внутри ямы не одинакова.

Классическая частица в яме может двигаться с любой энергией. Ее энергетический спектр непрерывен. Квантово-механические частица может двигаться в яме с определенной энергией (энергия частицы квантовая).

Зависит от главного квантового числа n E_пот=( ²ћ²n²)/(2ml²)

Ψ волновая функция 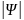²- плотность вероятности

Классическая частица может покоиться на дне ямы. Ее энергия может равняться 0.

4. Атомное ядро. Энергия связи. Дефект массы.

Показали, что масса ядра не равна сумме масс составляющих нуклонов

∆M=Z_тр+(A-Z)m_n-m_яд

Энергия связи это та энергия, которую необходимо сообщить ядру для разделения его на составляющиеся части или это работа, которую совершает ядерные силы для объединения нуклонов в ядро.

Билет № 17.

1. Вынужденные колебания пружинного маятника. Вынужденные колебания гармонического осциллятора, колебания которые он совершает под действием периодической внешней силы.

ma=∑F

mx’’=-kx-rx’+F₀cosωt; -kx-rx’- упругое трение; F₀cosωt- внешняя сила

x’’+2(r/m)x’+(k/m)x=(F₀/m)cosωt

x’’+2βx’+ω₀²x=(F₀/m)cosωt – дифференциальное уравнение ЗК

x(t)=x₀e^-βtcos(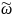 t+φ₀)+x₀ωcos(ωt-φ₀(ω))

Начальный процесс установлен ВК называется переходным режимом. Характеризуется временем релаксации = 1/β

Можно сказать:

1)Вынужденные колебания всегда происходят с частотой вынужденные силы

2)Вынужденные колебания всегда отстают по фазе от внешние силы

3)Амплитуда постоянна и пропорциональна амплитуде вынужденной силы

2. Интерференция электромагнитных волн. Бизеркала Френеля. Бипризма Френеля. Опыт Юнга.

В результате сложения когерентных волн одной и той же физической природы и одинаково поляризованных возникают стационарные волновые поля с резко неоднородной интенсивностью, называющиеся интерференционным волновым полем.

Области с max и min интенсивностью называются интерференционными полосами, а явления положения когерентных волн называется интерференцией.

3. Волны де Бройля и их статистическая интерпретация.

Де Бройль доказал, что все опыты в которых проявляются волновые свойства микрочастиц можно объяснить, если сопоставить движению свободной микрочастицы в волновую функцию вида :

Ψ(x,t)=A =Ae^-i(ωt-kx)=Ae^i/ћ(et-px);

E=ћω; p=ћk; ћ=h/2 - постоянная Планка

λ=2 /k=2 ћ/p=h/p; λ=h/p-длинна волны де Бройля микрочастицы

Борн предложил статистическое истолкование:IΨI²dV=dW

IΨI²=Ψ(r,t); Ψ(r,t)-плотность вероятности

4. Атом водорода, квантовые числа, вырожденные состояния.

Кратность вырожденных состояний в атоме водорода равно

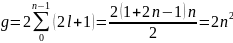
Билет № 18.

1. Затухающие колебания. Вывод дифференциального уравнения и его решение.

Колебания, при котором амплитуда (а следовательно и полная энергия) гармонического осциллятора лишенного притока энергии извне монотонно убывает с течением времени.

Физический смысл переход энергии гармонического осциллятора тепловую энергию окружающих тел.

Амплитуда убывает по экспоненциальному закону

ma=ΣА

mx’’=-kx-rx’

x’’+2(r/m)x’+ω₀²x=0

ω₀= β=r/(2m)- коэффициент затухания

x’’+2 β x’+ω₀²x=0 ;x(t)=x₀e^-βt(cos(ω^тильдаt+φ₀)); x₀e^-βt - амплитуда

Скорость затухания зависит от β.

2. Поглощение волн

Распространение волны в среде сопровождается явлением поглощения, то есть ослаблением интенсивности с расстоянием от источника.

Физический смысл: волна теряет энергию, превращая ее в энергию движения многих частиц, то есть происходит дисп. Энергии и по закону Ломбера-Бери интенсивность меняется по экспоненциальному закону I=I₀e^-µx

µ- коэффициент поглощения

µ зависит:

а)От природы волны

б)Физических и химических свойств среды

в)От температуры( при ^T, ^ µ)

г)От частоты волны

3. Корпускулярно волновой дуализм. Внешний фотоэффект, фотоны, электромагнитное изменение.

Определение фотоэффекта: вырывание электронов из кристалла под действием излучения.

Классическое объяснение

напряженность

Под действием периодической внешней сил электрон совершает вынужденные колебания.

Если увеличить интенсивность волны электроны оторвутся и вылетят из кристалла.

По классической трактовке энергия должна быть пропорциональна функции интенсивности волны.

Если менять длину волны до какой-то λ_кр наблюдение фотоэффекта, потом нет.

Для объяснении фотоэффекта и ряда других опытов было введено понятие о фотонах. Запишем закон сохранения энергии для взаимодействия фотона и электрона.

Фотон взаимодействует с электроном, отдает ему энергию электрона совершает работу для ылета и остальную энергию унесет.

Формула Эйнштейна для фотоэффекта

1.действительная энергия вылета электрона зависит от ν

2. ⇒

Фотоны – кванты электромагнитного излучения

4. Основное уравнение молекулярно-кинетической теории газов.

∆p=p₂-p₁=-2mV_x

f=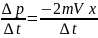 –сила действ. стенки на молекулу

Выберем площадь S подсчитаем сколько ударов за ∆t. Построим цилиндр с основанием Ы и высотой V_x∆t.Все молекулы в нем ударяются об него за ∆t.

N=nSV_x∆t/2; F=f*N=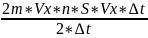 =mnV_x²S

P=F/S=mnV_x²; V²=V_x²+V_y²+V_z²

Т.к. хаотично, то V_x²=V_y²=V_z² средне

V²=3IV_x²I => p=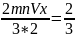 nW_{кин. ср}

Давление газа =2/3 средней кинетической энергии молекул содерж. В единице объема газа

N=N/V

P=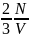 W_ср.кин.; pV=ѵRT

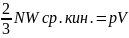
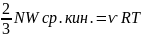=>2/3 N_aW_ср.кин.=RT; W_cр.кин.=(3/2)(R/N_а)T

Билет № 19.

1. Гармонические собственные колебания физического маятника.

Физический маятник- твердое тело, свободно вращающееся вокруг горизонтольной оси, не проходящей через центр инерции тела.

Iα’’=∑M

M=-mgsinα*L – как для математического маятника.

Т.к. углы малы то:

α’’+(mgL/i)α=0

ω_{0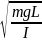 = 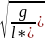;} l*-приведение длин маятника, это длина такого мат. Маятника, в котором такой же период l* используется для определения моментов инерции.

2. Дифракция Френеля на круглом отверстии на непрозрачный экран.

R- радиус круга

Радиус m-й зоны Френеля равен : r_m=

Если 0<R<r₁ интенсивность монотонно возрастает

r₁<R<r₂ монотонно уменьшается

r₂<R<r₃ монотонно возрастает

R=r₁ самое большое значение интенсивности

R=r₂ самое меньшее значение интенсивности

Если в отверстии непрозрачного экрана укладывается четное число зон Френеля, то в этой точке min освещенности , если нечетное – max.

Пусть теперь R=const и будет отодвигаться экран(в ↑) r_m=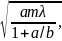 при ↑ b, r зон

Возрастает и поэтому R будет совпадать то с r четным, то с нечетным.

Понятие зон Френеля и анализ ВД показывает, что при данных значениях a,b,x можно существенно ↑ интенсивность точки P

3. Принцип тождественности микрочастиц, понятие о квантовой статистике.

Квантовая статистика основывается на принципе тождественности микрочастиц, согласно которому нельзя различать между собой отдельные микроскопические частицы и согласно кот состояние системы одинаковы частиц не меняется при обмене частиц местами.

4.Внутренняя энергия идеального газа, принцип равнораспределения энергии по степеням свободы молекул.

U_внутр.=(m/µ)*(i/2)*kT

Величина которая однозначно определяет состояние системы которое зависит от значения параметра определяет ее состояние и не зависит от пути и способа перевода в данное состояние называют функцией состояния.

∆u_внутр.= (m/µ)*(i/2)*k(T₂-T₁);

Во всех случаях мерой изменения u_внутр. является работа внешней силы.

∆u=A_внешн.

2 способ изменения внутренней энергии называется теплообменом. Теплообмен может осуществляется теплопроводностью, конвекцией, излучением.

Физ. Величина ∆u=Q количество теплоты

∆u=A_внешн.+Q

A_сист.=- A_внешн

∆u=Q- A_сист.

Билет № 20.

1.Сложение двух ортогональных гармонических колебаний кратных частот. Фигуры Лиссажу.

Пусть точка может совершать гармонические колебания как по оси х, так и по оси у. Если одновременно возбудить оба колебания, то точка будет двигать по некоторой кривой траектории. Нужно найти уравнение этой траектории.

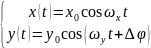
ω_x:ω_y=m:n

1)

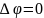
Чтобы получить уравнение траектории в явном виде мы должны исключить параметр t

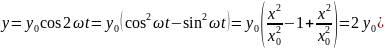
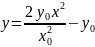- порабола

2)

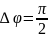
Замкнутые траектории, описываемые гармоническим осциллятором, при сложении двух ортогональных колебаний с кратными частотами называются фигурами Лиссажу. Они целиком заключены внутри прямоугольника со сторонами 2х₀ и 2у₀ и имеют число узлов (самопересечений) не превосходящее значение

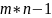
Фигуры Лиссажу используют для сравнения частот колебаний и установления соотношений между ними.

2.Дифракция Френеля, зоны Френеля, метод векторной диаграммы.

Все современные явления происходят при распределении волны в неоднородной среде в случае когда 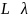. Сюда относительно огибания волновых препятствий, проникновение волны в область геометрической тени и т.д.

Здесь одного принципа Гюйгенса недостаточно и мы должны складывать вторые когерентные волы по принципу Френеля.

Рассмотрим свободное распределение сферической волны.

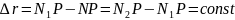
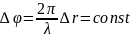
Воспользуемся методом векторной диаграммы:

Длина вектора изображает амплитуду волны зависящую от расстояния и убывает с ростом расстояния N_iP. Амплитуда волны уменьшается с увеличением угла α, убывает как cosα. Чтобы учесть все векторные пределы перейдем к пределу 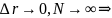векторная диаграмма сворачивается к центру и образует круглую спираль.

Зоны Френеля. Для удобства расчетов Френель предложил сгруппировать вторичные источники в более крупные области волнового фронта названными зонами Френеля.

Вторичные источники такие, что расстояние от краев каждой зоны до точки наблюдения отличаются на .

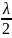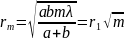
Если открыто четное число зон Френеля, то они взаимногасят друг друга в точке наблюдения и мы наблюдаем min освещенности в точке Р; если открыто нечетное число соседних зон Френеля, то одна зона оказывается нескомпенсированной и в точке Р наблюдается max освещенности.

Фаза колебаний возбужденная соседними зонами Френеля отличается на , поэтому результирующая амплитуда колебаний в точке Р может быть представлена: А=А₁ –А₂+А₃-А₄+…+А_m

Если четное, то “-“, нечетное – “+”.

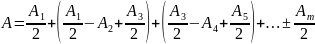
В случае монотонного убывания амплитуды А_m можно приближенно сосчитать, что 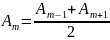, тогда выражение стоящее в скобках обращается в 0, тогда