
- •2. Принцип действия и конструкция однофазного и трехфазного тр-ра.
- •3. Конструкция ад. Схема замещения ад.
- •3 . Принцип работы ад.
- •2. Эдс, индуцируемые в обмотках статора и ротора.
- •3. Схемы замещения. Векторные диаграммы.
- •3) Энергетическая диаграмма асинхронного двигателя
- •3 . Коэффициент мощности и его зависимость от нагрузки ад.
- •Вопрос 2. Принцип действия машины постоянного тока в генераторном и двигательном режимах. Направление тока, эдс, электромагнитного момента.
- •Вопрос 3. Асинхронный двигатель с двойной «беличьей клеткой». Частотное регулирование частоты вращения ад. Как изменяется при этом механические характеристики.
- •3) Рабочие характеристики асинхронного двигателя
- •1. Комплексная мощность фазы генератора
- •2. Сравнение внешних характеристик гпт при различных способах возбуждения
- •3. Проанализируйте влияние реакции якоря на величину напряжения сг при неизменных эдс и тока статора при активной нагрузке. Изобразить соответствующую векторную диаграмму.
2. Эдс, индуцируемые в обмотках статора и ротора.
Действующее значение ЭДС, индуцированной в одном витке фазной обмотки, можно определить по той же формуле, что и в трансформаторе:
Е1в = 4,44fФm,
где Фт — максимальный магнитный поток, сцепленный
с витком, причем Фт = Bcpτl = -Bmxl;Bcp — среднее значение магнитной индукции на полюсном делении; х — полюсное деление (длина окружности статора, приходящаяся на один полюс); l — длина сердечника статора.
Действующее
значение комплексной ЭДС в фазной
обмотке будет равно: E1=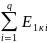 .
.
Действующее значение ЭДС фазной обмотки статора, индуцируемой вращающимся магнитным полем, равна
E1=4,44fω1kоб1Фm. Поскольку частота индуцируемой ЭДС пропорциональна частоте пересечения проводника вращающимся магнитным полем (в двигателе это n1), частота ЭДС статора: f1=pn1/60=60pf/60p=f , т. е. равна частоте напряжения сети.
В обмотке неподвижного ротора, по аналогии с обмоткой статора, индуцируется ЭДС такой же частоты
E2=4,44fω2kоб2Фm , где w2 — число витков обмотки фазы ротора, ko62 — ее обмоточный коэффициент.
В проводниках обмотки вращающегося ротора индуцируется синусоидальная ЭДС, имеющая частоту f2, равную
f2=pnS/60=psn1/60=sf, так как число полюсов ротора всегда равно числу полюсов статора.
ЭДС в обмотке вращающегося ротора: E2S=4,44f2ω2kоб2Фm=4,44sfω2kоб2Фm.
ЭДС вращающегося ротора можно выразить через ЭДС неподвижного ротора: E2S=sE2.
ЭДС обмотки ротора прямо пропорциональна скольжению или обратно пропорциональна частоте вращения ротора. Максимальное значение ЭДС ротора принимает при s= 1, т. е. при неподвижном роторе.
Отношение
ЭДС обмотки статора Е1
к
ЭДС обмотки неподвижного ротора Е2
обозначают
ke
и
называют коэффициентом
трансформации по ЭДС. Т.о. получаем:
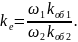 Величину
E2’=kеE2=E1
называют приведенной
ЭДС ротора.Она
в kе
раз
больше действительной ЭДС и равна ЭДС
статора.
Величину
E2’=kеE2=E1
называют приведенной
ЭДС ротора.Она
в kе
раз
больше действительной ЭДС и равна ЭДС
статора.
3. Схемы замещения. Векторные диаграммы.
С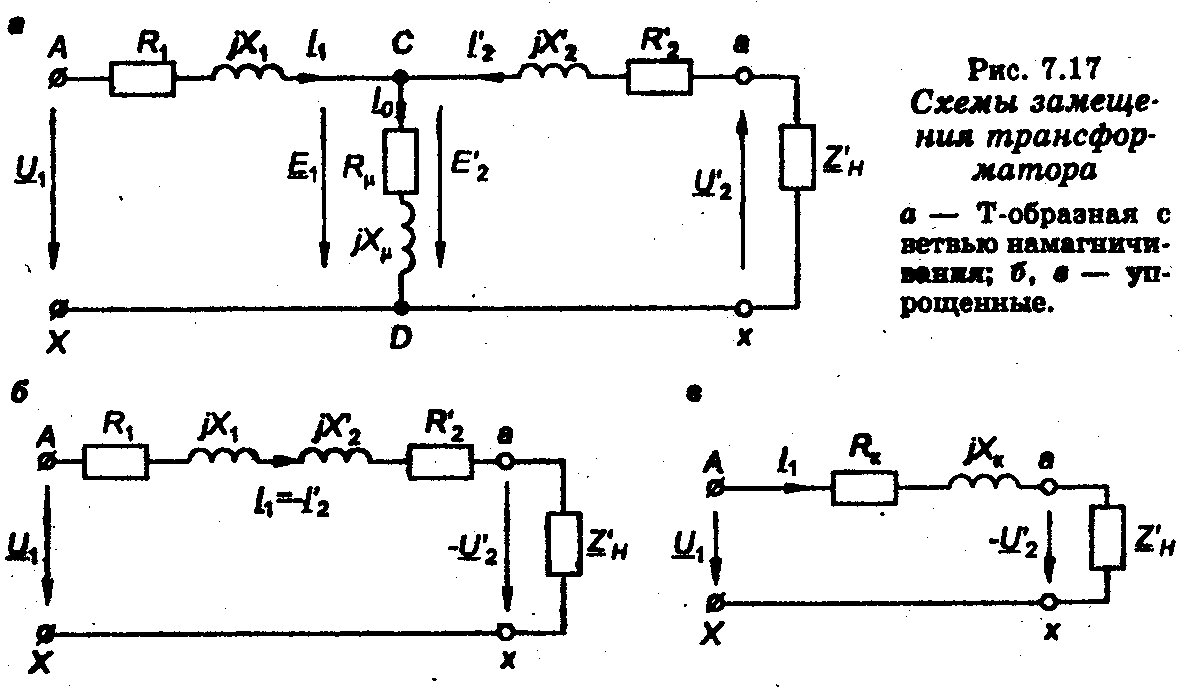
 хемой
замещения
трансформатора
называют электрическую схему,
эквивалентную действительной, в которой
все контуры электрически связаны
друг с другом. Параметрами такой цепи
являются параметры обмоток трансформатора
и взаимно индуктивной связи. Магнитный
поток рассеяния Ф1рас
индуцирует в первичной обмотке ЭДС
рассеяния
хемой
замещения
трансформатора
называют электрическую схему,
эквивалентную действительной, в которой
все контуры электрически связаны
друг с другом. Параметрами такой цепи
являются параметры обмоток трансформатора
и взаимно индуктивной связи. Магнитный
поток рассеяния Ф1рас
индуцирует в первичной обмотке ЭДС
рассеяния
Е1рас= -jX1L1, которую можно представить как падение напряжения с обратным знаком: ΔU1рас= -E1рас= jX1L1, где
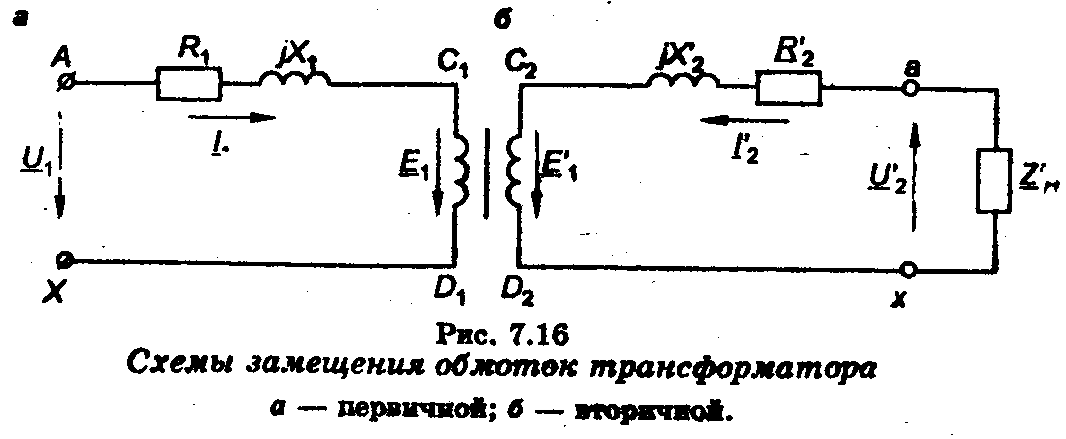
Х1 — индуктивное сопротивление первичной обмотки, обусловленное потоком рассеяния. Тогда первичная обмотка трансформатора может быть изображена на схеме включенными последовательно элементом с активным сопротивлением R1, равным активному сопротивлению проводов обмотки, элементом с индуктивным сопротивлением Х1 и элементом C1-D1 на зажимах которого основным магнитным потоком Ф индуцируется ЭДС Е1 (рис. 7.16а). К зажимам А-Х обмотки подводят напряжение U1.
Аналогично можно изобразить схему приведенной вторичной обмотки.
Так как Е2 и Е'2 равны по модулю и совпадают по фазе, то точки С1 и С2, D1 и D2 имеют соответственно равные потенциалы и их можно объединить в одну точку (точки С и D на рис. 7.17а). В результате получаем схему электрической связанной цепи, которая является схемой замещения трансформатора. Сопротивление Zμ ветви, на зажимах которой действуют ЭДС Е1 и Е'2, является сопротивлением ветви намагничивания, по которой замыкается ток I0, создающий магнитный поток Ф, индуцирующий эти ЭДС.
При токах нагрузки трансформатора, близких к номинальным, током I0 в ветви намагничивания, равным току холостого хода, можно пренебречь, что позволяет упростить схему замещения (рис. 7.17а), заменив ее схемой, представленной на рис. 7.176, в которой I1= -I2’.
Сложив активные и индуктивные сопротивления последовательно включенных элементов схемы (рис. 7.176), получим упрощенную схему замещения трансформатора (см. рис. 7.17в), в которой активное сопротивление Rk=R1+R2’, а индуктивное Xk=X1+X2’.
Векторную диаграмму строят на основании следующих уравнений:
U1= -E1+I1(R1+jX1)= -E1+I1Z1
U2’= E2’+I2’(R2’+jX2’)= E2’+I2’Z2’ (7.12)
I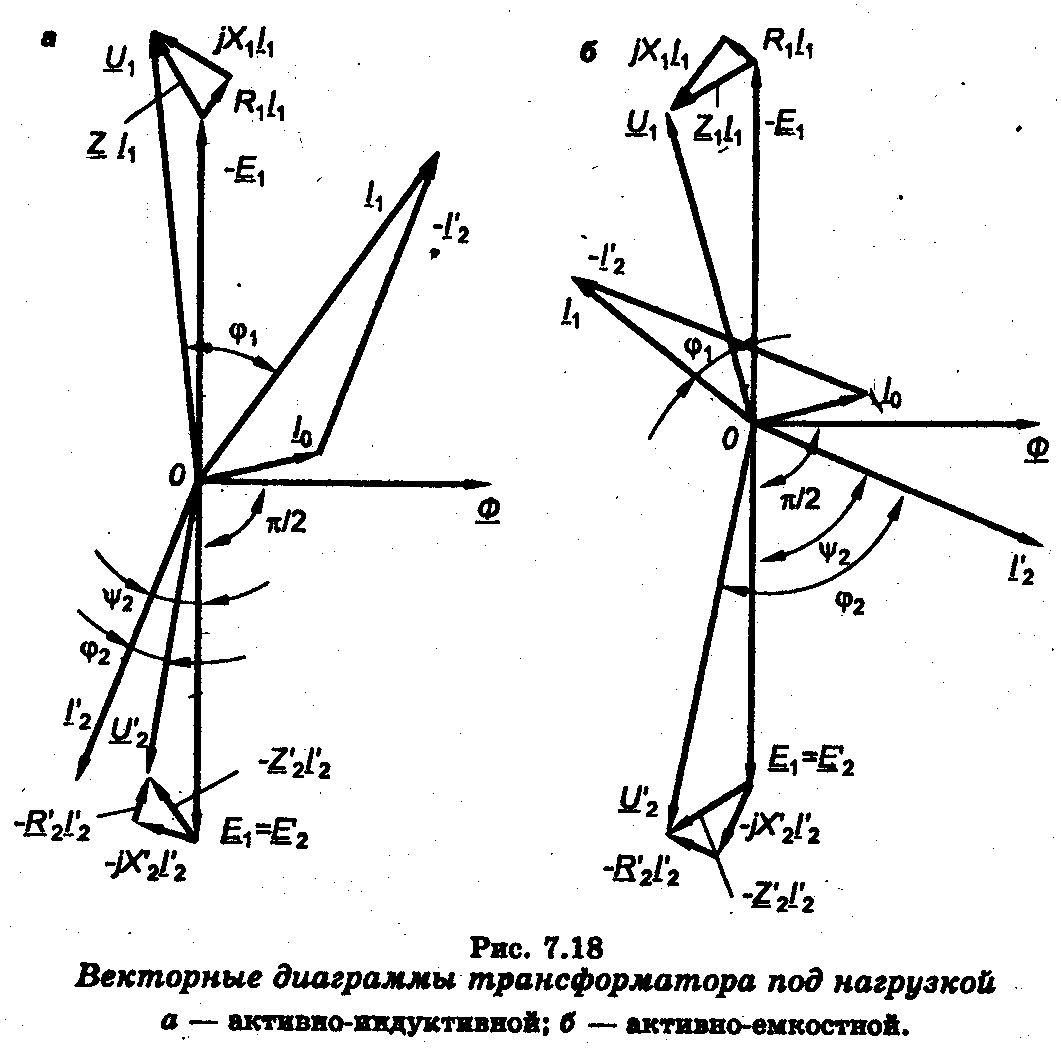 1=I0+(
-I2’)
1=I0+(
-I2’)
За начальный вектор удобнее принять вектор магнитного потока Ф (рис. 7.18), так как он является общим для обеих обмоток. Под некоторым углом в сторону опережения по фазе проводят вектор тока холостого хода 10. Затем под углом π/2 в сторону отставания проводят векторы ЭДС Е2 и Е'2, равные по значению. Дальнейшее построение векторной диаграммы определяется характером нагрузки, т. е. соотношением между активным, индуктивным и емкостным сопротивлениями нагрузки. При активно-индуктивном характере нагрузки вектор вторичного тока I2’, который одновременно является током нагрузки, проводят под углом ψ2 к вектору ЭДС Е'2 (см. рис. 7.18а), причем
Ψ2= arctg((X2’+Xн’)/( R2’+Rн’)), где Rн’ и Х'н — приведенные активное и индуктивное сопротивления нагрузки. Вектор вторичного напряжения U2’ находят из уравнения (7.12). Согласно этому уравнению, к вектору Е'2 необходимо прибавить векторы падения напряжения на активном и индуктивном сопротивлениях вторичной обмотки (с обратными знаками).
Поскольку вектор jХ'2I2’ падения напряжения на индуктивном сопротивлении опережает вектор тока I2’ на угол π/2, вектор -jХ'2 I2’с обратным знаком проводят в сторону отставания (рис. 7.18а). Затем от конца вектора -jХ'2 I2’ проводят вектор -R2’I2’, направленный противоположно вектору тока I2’. Вектор, соединяющий точку О с концом вектора -R2’I2’, и будет вектором вторичного напряжения U'2. Он опережает ток I2’ на угол φ2. Вектор первичного тока I1 находят из уравнения токов (7.12). К вектору тока холостого хода I0прибавляют вектор приведенного вторичного тока -I2’.
Построение векторной диаграммы заканчивают построением вектора первичного напряжения U1 который находят из уравнения (7.12). Для этого откладывают вектор ЭДС -Е1 а к нему пристраивают вектор падения напряжения на активном сопротивлении R1 первичной обмотки, параллельный вектору тока I1, и вектор падения напряжения на индуктивном сопротивлении Х1 первичной обмотки, опережающий вектор тока на угол π/2. Замыкающий вектор и будет вектором U1.
Билет 4
1) Значение переодически изменяющейся величины в рассматриваемый момент времени называют мгновенным ее значением и обозначают е, u, i – ЭДС, напряжение, ток
Мгновенное значение синусоидальной величины, например тока, определяют по формуле i = Imsin(ωt + ψ)
,![]() где ωt
+ ψ — фаза-угол,
определяющий значение синусоидальной
величины в данный момент времени; ψ
- начальная
фаза, т. е. угол, определяющий значение
величины в начальный момент времени.
где ωt
+ ψ — фаза-угол,
определяющий значение синусоидальной
величины в данный момент времени; ψ
- начальная
фаза, т. е. угол, определяющий значение
величины в начальный момент времени.
Синусоидальные величины, имеющие одинаковую частоту, но разные начальные фазы, называются сдвинутыми по фазе.
Разница начальных фаз φ = ψi − ψu определяет угол сдвига фаз. На рис. 2 приведены графики синусоидальных величин (тока, напряжения), сдвинутых по фазе. Когда же начальные фазы двух величин равны ψi = ψu, то разница ψi − ψu = 0 и, значит, сдвига фаз нет φ = 0 (рис. 3).
2) Опыт холостого хода - это определение реальных параметров элементов для используемых в расчетах схем замещения обычно активных двухполюсников, а именно при отсутствии внешней цепи можно определить величину ЭДС, так как из формулы закона Ома для полной цепи при сопротивлении внешнего участка стремящегося к бесконечности величина напряжения на клеммах реального элемента напряжение стремится к ЭДС, но следует учитывать соотношение внутреннего и внешнего сопротивлений внешнее сопротивление должно быть много больше внутреннего сопротивления источника, а на переменном токе следует учитывать реактивные составляющие сопротивления измерительного прибора.
По данным опыта холостого хода определяются коэффициент трансформации U2/U1≈ω2/ω1 магнитные потери Рс
и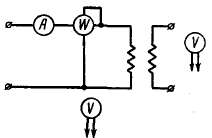 параметры ветви намагничивания Z12,
r12.
x12-
Магнитные
потери Рс,
как
указывалось, могут быть приняты равными
мощности Ро. потребляемой трансформатором
при холостом ходе.При опыте холостого
хода собирается схема по рис. 2-18 для
одно--фазного трансформатора или по
рис. 2-19 для трехфазного трансформатора.
При номинальном напряжении U1n(линейном
в случае трехфазного трансформатора)
измеряют I0
P0
и U20-
Опыт
холостого хода должен производиться
при синусоидальном напряжении. Если
напряжение заметно отличается от
синусоидального, то в данные измерений
необходимо внести некоторые поправки
(согласно ГОСТ). При исследовании малых
трансформаторов следует учитывать
потери в приборах, так как они могут
быть
соизмеримы с потерями холостого хода.
параметры ветви намагничивания Z12,
r12.
x12-
Магнитные
потери Рс,
как
указывалось, могут быть приняты равными
мощности Ро. потребляемой трансформатором
при холостом ходе.При опыте холостого
хода собирается схема по рис. 2-18 для
одно--фазного трансформатора или по
рис. 2-19 для трехфазного трансформатора.
При номинальном напряжении U1n(линейном
в случае трехфазного трансформатора)
измеряют I0
P0
и U20-
Опыт
холостого хода должен производиться
при синусоидальном напряжении. Если
напряжение заметно отличается от
синусоидального, то в данные измерений
необходимо внести некоторые поправки
(согласно ГОСТ). При исследовании малых
трансформаторов следует учитывать
потери в приборах, так как они могут
быть
соизмеримы с потерями холостого хода.
Рис. 2-18. Схема при опыте холостого хода для однофазного трансформатора.
Измерения U1 и U20 производятся при помощи вольтметров или при высоком напряжении при помощи вольтметров и измерительных трансформаторов напряжения. По данным измерений находят коэффициент трансформации: U20/U1≈ω2/ω1. По амперметру и ваттметру находят ток I0 и мощность Р0 в случае однофазного трансформатора. В случае трехфазного трансформатора необходимо измерить токи во всех трех фазах, так как вследствие несимметрии магнитных цепей отдельных фаз токи в них будут различны. За ток холостого хода здесь принимается среднее арифметическое токов отдельных фаз, т. е.
М![]() ощности
отдельных фаз также различны; поэтому
мощность, потребляемую трехфазным
трансформатором при холостом ходе,
следует измерять двумя ваттметрами по
схеме рис. 2-19.
ощности
отдельных фаз также различны; поэтому
мощность, потребляемую трехфазным
трансформатором при холостом ходе,
следует измерять двумя ваттметрами по
схеме рис. 2-19.
Для нормальных силовых трансформаторов ток холостого хода составляет (0,10—0,04)Iн при номинальных мощностях от 5 до нескольких тысяч киловольт-ампер.
Холостому ходу будет соответствовать схема замещения рис. 2-17 при Z' = ∞. Следовательно, по данным опыта холостого хода получаем:
z0=|Z1+Z12|=((r1+r12)^2+(x1+x12)^2)^1/2=U1/I0
Гак как для нормальных трансформаторов r12 больше r1 и х12 больше x1 в сотни раз, то можно принять:
z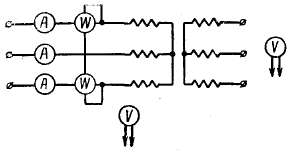 13≈z0
r12≈r0
=r1+r12=P0/I20
x12≈x0=(z20
–
r20)^1/2
13≈z0
r12≈r0
=r1+r12=P0/I20
x12≈x0=(z20
–
r20)^1/2
Рис. 2-19. Схема при опыте холостого хода для трехфазное трансформатора.
