Интерполяционные квадратурные формулы наивысшей алгебраической степени точности (квадратурные формулы Гаусса - Кристоффеля)

Точность интерполяционной квадратурной формулы можно существенно повысить путем рационального выбора узлов . Задача получения более точной квадратурной формулы формулируется следующим образом:

построить квадратурную формулу

, (8)

которая при заданном была бы точной для полиномов возможно большой степени. Обратите внимание, что в формуле (8) для удобства изложения нумерация узлов начинается с . Построение такой формулы заключается в надлежащем выборе коэффициентов и узлов . Такие формулы существуют. Они называются квадратурными формулами наивысшей алгебраической степени точности или квадратурными формулами Гаусса – Кристоффеля или квадратурными формулами Гаусса. Эти формулы точны для любого алгебраического многочлена степени .

Таким образом, для любых существует, причем единственная, квадратурная формула наивысшей алгебраической степени точности вида(8).Узлы этой формулы совпадают с корнями ортогонального на с весом полинома степени , а коэффициенты определяются формулой:

Узлы и соответствующие им веса квадратурной формулы Гаусса рассчитываются заранее для различных весовых функций и сводятся в таблицу. Приведем пример квадратурной формулы Гаусса.

Квадратурная формула Гаусса-Лежандра

Квадратурная формула Гаусса-Лежандра используется для вычисления интеграла с единичной весовой функцией =1 на конечном отрезке , т.е. интеграл вида

Этот интеграл линейной заменой переменных

приводится к виду

=

На отрезке ортогональны с весом =1 полиномы Лежандра

.

Узлы квадратурной формулы в этом случае выбираются равными корням полинома Лежандра . Квадратурная формула имеет вид

В таблице в качестве примера приведены узлы и коэффициенты для этой формулы при использовании двух, трех и четырех узлов.

Таблица – Узлы и коэффициенты квадратурной формулы Гаусса-Лежандра

Число узлов	Значение улов	Значение весовых коэффициентов
2	0,577350	1
3	0 0,774597
4	0,339981 0,861136	0,652145 0,347855

Рассмотрим данные методы на примере.

Вычислим . Этот интеграл сводится к табличному и он равен , его значение:

Разобьем отрезок интегрирования [0,1] на 5 равных частей (5 частичных отрезков). Количество узлов – 6.В нашем случае a = 0, b = 1. Вычислим h.

h = 0, 2.

Интегрируемая функция

Вычислим значения функции в узлах: 0; 0,2; 0,4; 0,6; 0,8; 1.

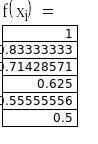
Для оценки погрешности вычислим производные 1, 2 и 4 – го порядка:

Максимальное по абсолютной величине значение на отрезке [0,1] производные достигают в точке x = 0.Соответственно, .

Вычислим интеграл методом левых прямоугольников.

За узлы интегрирования возьмем точки: 0; 0,2; 0,4; 0,6; 0,8. h = 0,2.

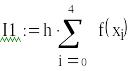
Погрешность интегрирования оценивается выражением:

Вычислим интеграл методом правых прямоугольников.

За узлы интегрирования возьмем точки: 0,2; 0,4; 0,6; 0,8; 1. h = 0,2.

Вычислим интеграл методом трапеций.

За узлы интегрирования возьмем точки: 0; 0,2; 0,4; 0,6; 0,8; 1. h = 0,2.

Погрешность метода оценивается выражением:

Разобьем отрезок интегрирования [0,1] на 10равных частей (n = 10), вычислим интеграл методом трапеций при h1 = 0, 1 и оценим полученный результат по правилу Рунге.

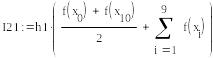
Погрешность вычисления интеграла оценивается выражением:

Вычислим интеграл по квадратурной формуле интерполяционного типа.

Возьмем 3 узла: 0; 0,5; 1.Функция f(x) на отрезке [0, 1] заменяется параболой (n = 2). Квадратурная формула интерполяционного типа, построенная на узлах 0; 0,5; 1 совпадает с формулой Симпсона.h = 0,5.

Погрешность интегрирования оценивается выражением:

Вычислим интеграл методом средних прямоугольников.

За узлы интегрирования возьмем середины частичных отрезков, т. е точки: 0,1; 0,3; 0,5; 0,7; 0,9. Вычислим значения функции в узлах интегрирования.

Для этого разобьем отрезок интегрирования [0,1] на 10 равных частей.

h1 = 0, 1. h =2*h1 = 0, 2.

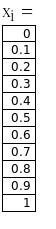
Погрешность оценивается выражением:

Вычислим интеграл методом Симпсона.

Отрезок интегрирования [0,1] разбивается на 2n = 10 равных частей. h =h1=0, 1.

Погрешность интегрирования методом Симпсона оценивается выражением:

Вычислим интеграл по формулам Гаусса – Кристоффеля.

При n =2:

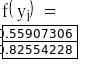
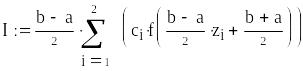
При n = 3:

При n = 4:

Задание:

1. Вычислить точное значение интеграла согласно варианту.

2. Вычислить определенный интеграл одним из методов согласно варианту при ( - число частичных отрезков, количество узлов ). В методе Симпсона .

3. Методом неопределенных коэффициентов построить интерполяционную квадратурную формулу на 4 равностоящих узлах, вычислить интеграл.

4. Вычислить интеграл по формуле Гаусса - Кристоффеля на 3 и 4 узлах соответственно.

5. Оценить реальную и ожидаемую погрешность (в т.ч. по правилу Рунге).

6. Самостоятельно сделать выводы.

Варианты:

№ №	Определенный интеграл	Методы
1.		средних прямоугольников, трапеций
2.		парабол (Симпсона), трапеций
3.		парабол (Симпсона), правых прямоугольников
4.		средних прямоугольников, парабол (Симпсона)
5.		парабол (Симпсона), трапеций
6.		средних прямоугольников, правых прямоугольников
7.		парабол (Симпсона), трапеций
8.		средних прямоугольников, трапеций
9.		парабол (Симпсона), левых прямоугольников
10.		парабол (Симпсона), трапеций
11.		средних прямоугольников, парабол (Симпсона)
12.		парабол (Симпсона), средних прямоугольников.