39.Уравнение состояния идеального газа. Закон Дальтона.

для одного моля газа.

Используя зависимость давления идеального газа от его температуры и концентрации молекул p = nkT ,

можно найти связь между основными макроскопическими параметрами газа — объемом V, его давлением p и температурой T.    Концентрация n молекул газа равна  , (26.1)

где N — число молекул газа в сосуде объемом V. Число N можно выразить как произведение количества вещества   на постоянную Авогадро N_A:  . (26.2)

Из выражений (25.9), (26.1) и (26.2) получаем  . (26.3)

Произведение постоянной Авогадро N_A на постоянную Больцмана k называется молярной газовой постоянной R. Молярная газовая постоянная равна  . (26.4)

Используя молярную газовую постоянную, выражение (26.3) преобразуем в уравнение  . (26.5)

Количество вещества   можно найти, зная массу вещества m и его молярную массу M:  , (26.6)

поэтому уравнение (26.5) можно записать в такой форме: . (26.7)

Законы Дальтона — два физических закона, определяющих суммарное давление и растворимость смеси газов. Сформулированы Джоном Дальтоном в начале XIX века.

40.Молекулярно-кинетическая теория газов (мкт) .Уравнение мкт идеального газа.

Задача молекулярно–кинетической теории – вывести все свойства вещества из его молекулярно-кинетической модели. Модель эта содержит представления о свойствах молекул вещества, их движении и взаимодействии. Представления, естественно, уточняются с развитием науки, поэтому уточняется и модель.

Основные положения этой модели следующие:

• газ состоит из молекул (мельчайших частиц, размеры которых ˜ 10^-10м.)

• молекулы газа находятся в непрерывном хаотическом движении.

• молекулы сталкиваются друг с другом. Столкновения бывают упругими (низкие температуры) и неупругими (высокие температуры)

• в промежутке между соударениями молекулы движутся прямолинейно

• молекулы на малых расстояниях отталкиваются, а на больших притягиваются друг к другу.

Следует заметить, что внутренняя структура самой молекулы описывается квантовой физикой. Включение в описание явлений внутреннего строения молекул, является дальнейшим уточнением модели.

  которое выглядит так:  , где р — давление идеального газа, m0 — масса молекулы,  среднее значение

  МКТ идеального газа в виде: 

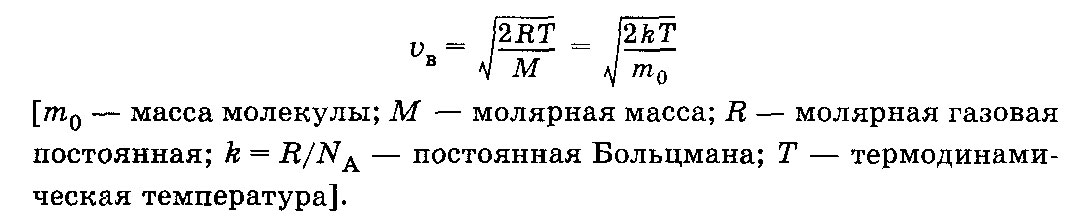
кв. скорость=корень из(3RT/M) 

41.Закон равномерного распределения энергии по степеням свободы.

Согласно молекулярно-кинетической теории газов движение молекул носит беспорядочный характер; эта беспорядочность относится ко всем видам движения молекулы. Ни один из видов движения не имеет преимущества перед другим. При статистическом равновесии движений энергия в среднем распределяется равномерно между всеми видами движения. Закон равномерного распределения энергии по степеням свободы молекул можно сформулировать следующим образом: статистически в среднем на каждую степень свободы молекул приходится одинаковая энергия. Поступательное движение молекул характеризуется средней кинетической энергией, равной   . Так как поступательному движению соответствует 3 степени свободы, то в среднем на одну степень свободы движения молекул приходится энергия

В однородном газе, молекулы которого имеют любое число степеней свободы i, каждая молекула в среднем обладает энергией движения, равной