Закон изменения момента импульса.

 

Рассмотрим произвольную систему тел. Моментом импульса системы назовем величину L, равную векторной сумме моментов импульсов отдельных ее частей L_i, взятых относительно одной и той же точки выбранной системы отсчета.               L = ΣL_i. Найдем скорость изменения момента импульса системы. Проведя рассуждения, аналогичные описанию вращательного движения твердого тела, получим, что скорость изменения момента импульса системы равна векторной сумме моментов внешних сил M, действующих на части этой системы.      dL/dt = M.                                                      

Причем вектора L и M задаются относительно одной и той же точки O в выбранной СО. Уравнение (21) представляет собой закон изменения момента импульса системы.Причиной изменения момента импульса является действующий на систему результирующий момент внешних сил. Изменение момента импульса за конечный промежуток времени можно найти, воспользовавшись выражением            .                                           Приращение момента импульса системы равно импульсу результирующего момента внешних сил, действующих на нее.В неинерциальной системе к моменту внешних сил необходимо прибавить момент сил инерции относительно выбранной точки O.

14.Динамика вращения материальной точки относительно оси.

Рассмотрим движение твердого тела, имеющею ось вращения   под действием произвольно направленной силы  , приложенной к телу в некоторой точке А , которую можно разложить на две составляющие: вертикальную и горизонтальную (рис.5.1). Вертикальная составляющая может вызывать перемещение тела в направлении оси вращения поэтому при рассмотрении вращательного движения ее можно исключить.Горизонтальная составляющая  , если она не пересекается с осью   вызывает вращение тела. Действие этой силы зависит от ее числового значения и расстояния линии действия от оси вращения.

15.Динамика твердого тела ,вращающегося около неподвижной оси. Момент инерции тела

Согласно второму закону Ньютона, для тангенциальной составляющейсилы  , действующей на материальную точку массой m, и ускорения  можем записать  и  имеем Домножимлевую и правую части на  и получим

или Произведение массы материальной точки   тела на квадрат ее расстояния   до оси вращения называется моментом инерции материальной точки относительно оси вращения:

16.Теорема Штейнера.

Момент инерции тела J относительно произвольной оси равен моменту инерции Jc относительно параллельной оси проходящей через центр масс С тела ,сложенному с произведением массы m тела на квадрат расстояния a между ними . J=Jc+m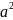

17.примеры расчетов моментов инерции тел прав геометр формы: тонкостенный цилиндр ,сплошной цилиндр.

Полый тонкостенный цилиндр или кольцо радиуса r и массы m

Ось цилиндра

	Сплошной цилиндр или диск радиуса r и массы m	Ось цилиндра
	Сплошной цилиндр длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс
	Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m	Ось перпендикулярна к цилиндру и проходит через его центр масс

18.Однородный тонкий стержень.

	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его центр масс
	Прямой тонкий стержень длины l и массы m	Ось перпендикулярна к стержню и проходит через его конец

19.Работа силы. Мощность. Изменение механического движения и энергии тела происходит в процессе силового взаимодействия этого тела с другими телами. Для количественной характеристики этого процесса в механике вводят понятие работы, совершаемой силой.

Если рассматриваемая сила   постоянна,а тело, к которому она приложена, движется поступательно и прямолинейно, то работой, совершаемой силой   при прохождении телом пути  , называют величину

(4.1)

где а - угол между силой   и направлением движения тела.

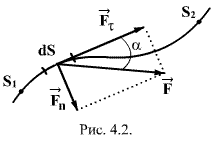
Работа - скалярная величина. Если вектор силы и вектор перемещений образуют острый угол т.е.  , то  , если  , то  , т.е. сила, действующая перпендикулярно к перемещению тела, работы не совершает.В общем случае тело может двигаться произвольным, достаточно сложным образом (рис.4.2). Выделим элементарный участок пути  , на котором силу можно считать постоянной и перемещение прямолинейным. Элементарная работа на этом участке равна

(4.2)

Полная работа на пути  определяется интегралом

(4.3)

Мощность- Величина, характеризующая скорость совершения работы, называется мощностью Мощность численно равна отношению   к промежутку времени   за который она совершается. или в общем случае ,Подставляя значение   получим