
Функциональные отношения.
Определение. Бинарное отношение
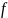 заданное на множестве
называется функциональным, если из
заданное на множестве
называется функциональным, если из
 всегда следует, что
всегда следует, что
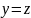 .
.
Определение. Функциональным отношением называется бинарное отношение, в котором нет двух упорядоченных пар, в которых первые координаты равны, а вторые различны.
Определение. Бинарное отношение
называется
функциональным на множестве
,
если для каждого элемента
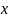 существует единственный элемент
,такое
что (
существует единственный элемент
,такое
что (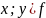 .
.
Поскольку элемент y
определяется однозначно, то будем
обозначать
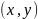 .
.
Определение. Если
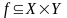 ,то
,то
 называется областью,
называется областью,
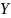 - кообластью.
- кообластью.
Определение. Областью определения
функционального отношения
называется множество всех первых
координат
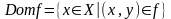 .
.
Определение. Областью значения
называется множество всех вторых
координат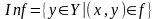 .
.
Свойства функциональных отношений.
1
Y
X
 .
.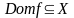
2 .
.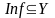

Определение.
Функциональное отношение
называется функцией (отображением),
если
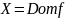 (если область равна области определения).
(если область равна области определения).
Самый
прямой способ задать функцию – это
задать с помощью списка значений, которые
она принимает на элементах области.
Например, одна из функций с областью
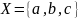 ,
кообластью
,
кообластью
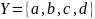 и
образом f
и
образом f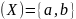 задается предписанием
задается предписанием
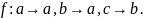
Другая
функция
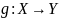 с образом
с образом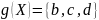 задается предписанием
задается предписанием
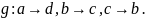
В
качестве другого примера определим
функцию следования Пеано
,
для которой множество
 всех положительных целых чисел является
и областью и кообластью. Каждому целому
положительному числу
она ставит в соответствие число
всех положительных целых чисел является
и областью и кообластью. Каждому целому
положительному числу
она ставит в соответствие число
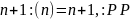 – функция из
в
.
Функцию
также можно задать (бесконечным) списком
предписаний:
– функция из
в
.
Функцию
также можно задать (бесконечным) списком
предписаний:
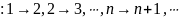
Очевидно,
образом
 функции
функции
 является множество
является множество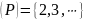 ,
которое мы обозначим символом
,
которое мы обозначим символом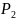 .
.
Итак, чтобы задать функцию необходимо определить ее область, кообласть и значения, которые она сопоставляет каждому элементу области.
Определение.
Если
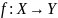 и
и
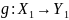 ,
то
,
то
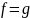 тогда и только тогда, когда
тогда и только тогда, когда
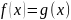 для всех
для всех
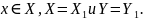
Определение.
Для любого множества
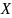 тождественная функция
тождественная функция
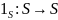 отображает любой элемент области
в себя:
отображает любой элемент области
в себя:
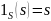 для всех
для всех
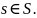 В силу вышесказанного тождественные
функции неравных множеств различны.
В силу вышесказанного тождественные
функции неравных множеств различны.
Основные свойства функциональных отношений.
(Лекция 5.)
1.
Иньективность. Если из
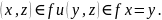
2.
Сюрьективность. Если
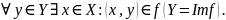
3. Функциональное отношение называется взаимно-однозначным, если оно инъективно и сюрьективно. Если при этом - функция то оно биективное.
Определение.
Пусть
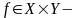 функциональное
отношение, тогда бинарное отношение
функциональное
отношение, тогда бинарное отношение
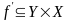 называется
инверсным, если
называется
инверсным, если
 .
Бинарное отношение
.
Бинарное отношение
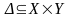 называется главной диагональю, если
для любого
называется главной диагональю, если
для любого
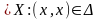 .
.
Пример. Проверить, является ли
бинарное отношение функциональным.
Установить его свойства:
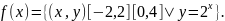
Решение.
Функциональное отношение. Из
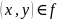 и
и
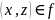 ,
следует, что
.
,
следует, что
.
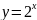 и
и
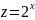 следует, что
– верно.
следует, что
– верно.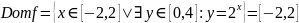 – отображение.
– отображение.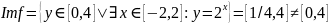 - не сюрьективно.
- не сюрьективно.Инъективность. Из и
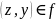 ,
следует, что
,
следует, что
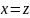 .
и
.
и
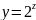 следует, что
– верно.
следует, что
– верно.
 – инъективное отображение.
– инъективное отображение.
Свойства инверсного отношения
и главной диагонали.
Теорема.
Пусть
– функциональное отношение,
- главная диагональ и
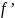 – инверсное отношение. Тогда справедливы
следующие свойства:
– инверсное отношение. Тогда справедливы
следующие свойства:
Функциональное отношение рефлексивно тогда и только тогда, когда
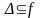 .
.Функциональное отношение антирефлексивно тогда и только тогда, когда
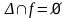 .
.Функциональное отношение симметрично тогда и только тогда, когда
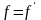 .
.Функциональное отношение антисимметрично тогда и только тогда, когда
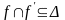 .
.
Доказательство.
1.
Пусть
рефлексивно, тогда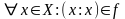 с другой стороны
с другой стороны
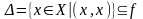 .
.
2.
Пусть
антирефлексивно, тогда
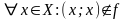 .
По определению
.
По определению
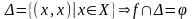 .
.
3.
Пусть
– симметрично тогда, из
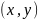
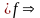
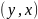
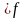 т.к
т.к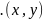
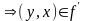
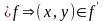
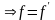 .
.
4.
Пусть
– антисимметрично.
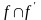 :
: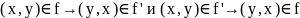 .
Из чего следует, что
.
Из чего следует, что
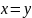 .
.
Композиция функциональных отношений.
Определение.
Пусть
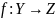 и
левой композицией функций
и
и
левой композицией функций
и
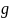 называется новая функция
называется новая функция
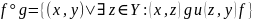 .
.
Аналогично определяется правая композиция функций.
Следствие.
Если
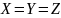 ,то
,то
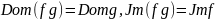 ,
причем из (
,
причем из (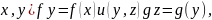 и следует, что
и следует, что
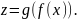
Теорема.
Композиция функциональных отношений
подчиняется ассоциативному закону:
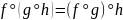 .
.
Доказательство. Пусть
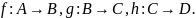 Любому элементу
Любому элементу
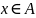 обе композиции приписывают значения
обе композиции приписывают значения
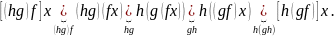
Проверка каждого равенства состоит в применении определения 6.12. к той композиции, которая указана под знаком равенства.
Определение.
Тождественным функциональным
отношением называется такое функциональное
отношение
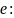
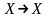 ,
что
,
что
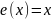 ,
,
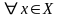 .
.
Свойства тождественного функционального отношения.
Теорема.
Пусть

 “º”- композиция
“º”- композиция
1.
Если
 ,то
,то
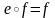 .
.
2.
Если
,
то
 .
.
3.Пусть
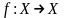 и
и
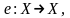 тогда
тогда
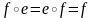 .
.
Доказательство.
1.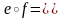 и
и
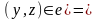 и
и
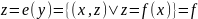 .
.
2.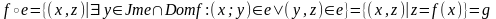 .
.
Обратные функциональные отношения.
Пусть - некоторая функция.
Определение.
Функция
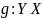 называется левой обратной функцией,
если
называется левой обратной функцией,
если
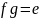 ,
и правой обратной, если
,
и правой обратной, если
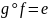 .
.
Определение.
Если функция
является левой и правой обратной функции
,
то функция
называется обратимой, а функция
двусторонне обратимой к
.
Обозначение:
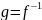 .
.
Теорема.
Пусть
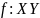 – функция,
– функция,
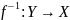 :
– обратная функция. Тогда справедливы
следующие свойства:
:
– обратная функция. Тогда справедливы
следующие свойства:
1. .
.
2.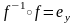 .
.
Теорема. Функция обратима слева тогда и только тогда, когда она инъективна. Функция обратима справа тогда и только тогда, когда она сюрьективна.
Доказательство. Пусть
- функция, обратная слева к
.
Предположим, что
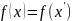 .
Тогда
.
Тогда
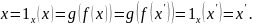
Таким образом, из предположения, что
,
получили, что
 .
Это доказывает инъективность.
.
Это доказывает инъективность.
Проверим обратное утверждение. Требуется
доказать, что если
инъективна, то у нее существует левая
обратная функция
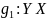 такая что,
такая что,
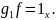 Для этого выберем элемент
Для этого выберем элемент
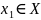 и определим
и определим
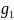 следующим образом:
следующим образом:
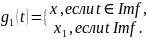
Тогда
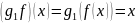 для всех
для всех
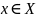 ,
так что,
является левой обратной к f.
,
так что,
является левой обратной к f.
Аналогично. Если
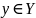 и
и
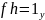 ,
то
,
то
 так что любой элемент
является образом
так что любой элемент
является образом
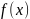 подходящего элемента
подходящего элемента
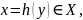 и
сюръективна.
и
сюръективна.
Обратно, если
сюрьективна, то каждый элемент
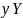 является образом
является образом
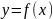 хотя бы одного элемента
.
Для каждого элемента
хотя бы одного элемента
.
Для каждого элемента
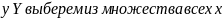 ,
переходящих в
,
один представитель и обозначим его
через
,
переходящих в
,
один представитель и обозначим его
через
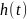 .
Тогда получим функцию
.
Тогда получим функцию
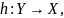 такую, что
такую, что
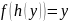 для всех
,
т.е.
для всех
,
т.е.
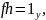 как утверждалось.
как утверждалось.
Следствие. Функция является биекцией тогда и только тогда, когда она обратима слева и справа.
Теорема. Следующие свойства функции эквивалентны:
– биекция;
обладает левой обратной g и правой обратной h;
Если эти свойства выполняются, то
все обратные к функции (левые, правые и двусторонние) совпадают. Эта единственная обратная к функция
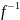 биективна, и
биективна, и
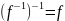 .
.
Доказательство. Эквивалентность
свойств I. и II.
является просто переформулировкой
следствия. Из условия II.
вытекает, что
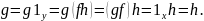
Это показывает, что все левые и правые,
обратные к f функции
совпадают, и доказывает III.
Наконец, биективная функция f
обратна к своей обратной функции
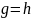 ,
либо
,
либо
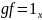 и
и
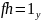 .
Следовательно, обратная функция биективна
и имеет
в качестве своей единственной обратной,
т.е.
.
.
Следовательно, обратная функция биективна
и имеет
в качестве своей единственной обратной,
т.е.
.
Аксиомы Пеано. Метод математической индукции.
Множество натуральных чисел.
(Лекция 6.)
Понятие натурального числа связано с количеством некоторой совокупности объектов.
Поскольку количество объектов можно сравнивать относительно бинарного отношения > или <, то совокупность натуральных чисел можно разместить в порядке возрастания – называется рядом натуральных чисел, тогда по отношению к ряду натуральных чисел можно задать понятие “непосредственно следовать за в натуральном ряду”.
Если n – некоторое натуральное число, то n’ – число “непосредственно следующее за n в натуральном ряду”.
Аксиома
1. Существует наименьшее натуральное
число
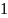 ,
которое непосредственно не следует ни
за одним натуральным числом.
,
которое непосредственно не следует ни
за одним натуральным числом.
– наименьшее натуральное число такое,
что для
натурального числа
неверно, что
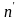
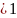 .
.
Аксиома
2. Для любого натурального числа
существует единственное натуральное
число, непосредственно следующее за
в натуральном ряду. Для
натурального числа
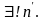
Аксиома
3. Для любого натурального числа
существует не более одного натурального
числа
 такого что
такого что
 .
.
Аксиома
4. (Аксиома индукции) Если
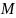 - некоторое множество натуральных чисел
и для
выполняется
- некоторое множество натуральных чисел
и для
выполняется
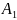 и
и
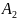 ,
то
множество всех натуральных чисел.
,
то
множество всех натуральных чисел.
Определение.
Множество натуральных чисел удовлетворяющих
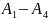 называется множеством всех натуральных
чисел и обозначается
называется множеством всех натуральных
чисел и обозначается
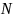 .
.
Принцип математической индукции.
Определение.
Для некоторого утверждения
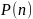 натурального аргумента, множество всех
натуральных чисел, для которых утверждение,
верно, называется областью истинности
утверждения
.
Обозначение:
натурального аргумента, множество всех
натуральных чисел, для которых утверждение,
верно, называется областью истинности
утверждения
.
Обозначение:
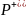 .
.
Если
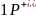 и из
и из
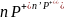 ,
то
,
то
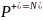 .
.
Метод математической индукции.
Пусть задано некоторое утверждение на множестве всех натуральных чисел, тогда требуется проверить справедливость утверждения на множестве всех натуральных чисел , для этого:
Проверим что
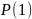 - верно.
- верно.Полагаем что - верно.
Два вместе взятых пункта 1 и 2 называются базисом индукции
Индукция: Из пунктов один и два проверяем, что
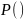 - верно.
- верно.
Вывод.
Если выполняется 1 и 3, то основе
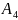 ,
следует, что
- верно для любого
,
следует, что
- верно для любого
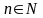 .
.
Если определить множество натуральных чисел, которое начинается с любого другого числа кроме 1, то методом математической индукции позволяет проверять справедливость любого утверждения на этом множестве, для этого в первом пункте проверяют справедливость утверждения для наименьшего элемента рассматриваемого множества.
Пример: Доказать методом математической индукции:
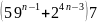 .
.
Решение. Методом математической индукции:
Для
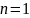 :
:
 - верно.
- верно.Предположим, что для
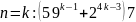 .
.Проверим, что для
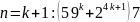 .
Так как
.
Так как
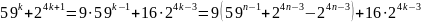 =
=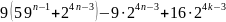 =
=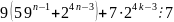 .
.
