
- •Министерство образования Российской Федерации
- •Остаток ряда.
- •Ряды с неотрицательными членами.
- •Интегральный признак Коши.
- •Признаки сравнения.
- •Признак Даламбера.
- •Радикальный признак Коши.
- •Признак Лейбница.
- •Свойства абсолютно сходящихся рядов.
- •Равномерная сходимость функционального ряда.
- •Признак Вейерштрасса.
- •Свойства равномерно сходящихся рядов.
- •Свойства степенных рядов.
- •Разложение в степенной ряд некоторых элементарных функций.
- •Применение степенных рядов.
- •Свойства двойных интегралов.
- •Тройной интеграл.
- •Геометрический смысл двойного интеграла.
- •Вычисление двойного интеграла в полярных координатах.
Геометрический смысл двойного интеграла.
Р

 ассмотрим
телоV, ограниченное
частью поверхности, задаваемой уравнениемz = f(x,
y),проекциейD
этой поверхности на плоскость Оху
и боковой цилиндрической поверхно-стью,
полученной из вертикальных образующих,
соединяющих точки границы поверх-ности
с их проекциями.
ассмотрим
телоV, ограниченное
частью поверхности, задаваемой уравнениемz = f(x,
y),проекциейD
этой поверхности на плоскость Оху
и боковой цилиндрической поверхно-стью,
полученной из вертикальных образующих,
соединяющих точки границы поверх-ности
с их проекциями.
 z=f(x,y)
z=f(x,y)



 z
z




 V
V

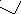
 y
• Pi
D
Рис.2.
y
• Pi
D
Рис.2.
Будем
искать объем этого тела как предел суммы
объемов цилиндров, основаниями которых
являются части ΔSi
областиD, а высотами
– отрезки длинойf(Pi),
где точкиPi
принадлежат ΔSi.
Переходя к пределу при![]() ,
получим, что
,
получим, что
![]() (7.12)
(7.12)
то есть двойной интеграл представляет собой объем так называемого цилиндроида, ограниченного сверху поверхностью z = f(x, y), а снизу – областьюD.
Лекция 8.
Вычисление двойного интеграла путем сведения его к повторному. Вычисление двойного интеграла в полярной системе координат.
Р
 ассмотрим
областьD, ограниченную
линиями
ассмотрим
областьD, ограниченную
линиями![]() x = a,
x = b
(a < b), где φ1(х) и φ2(х)
непрерывны на [a, b].
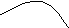
Тогда любая прямая, параллельная
координатной оси Оуи проходящая
через внутреннюю точку областиD,
пересекает границу области в двух
точках:N1иN2(рис.1). Назовем такую областьправильной
в на-
x = a,
x = b
(a < b), где φ1(х) и φ2(х)
непрерывны на [a, b].
Тогда любая прямая, параллельная
координатной оси Оуи проходящая
через внутреннюю точку областиD,
пересекает границу области в двух
точках:N1иN2(рис.1). Назовем такую областьправильной
в на-
у правлении оси Оу. Аналогично определя-
y=φ2(x) ется область, правильная в направлении
 N2
оси Ох. Область,
правильную в направле-
N2
оси Ох. Область,
правильную в направле-

 нии обеих координатных осей, будем
на-
нии обеих координатных осей, будем
на-


 D
зывать просто
правильной. Например,
D
зывать просто
правильной. Например,
правильная область изображена на рис.1.
y=φ1(x)N1
O a b x
Рис.1
Пусть функция f(x, y)непрерывна в областиD. Рассмотрим выражение
 ,
(8.1)
,
(8.1)
называемое двукратным интеграломот функцииf(x, y)по областиD. Вычислим вначале внутренний интеграл (стоящий в скобках) по переменнойу, считаяхпостоянным. В результате получится непрерывная функция отх:
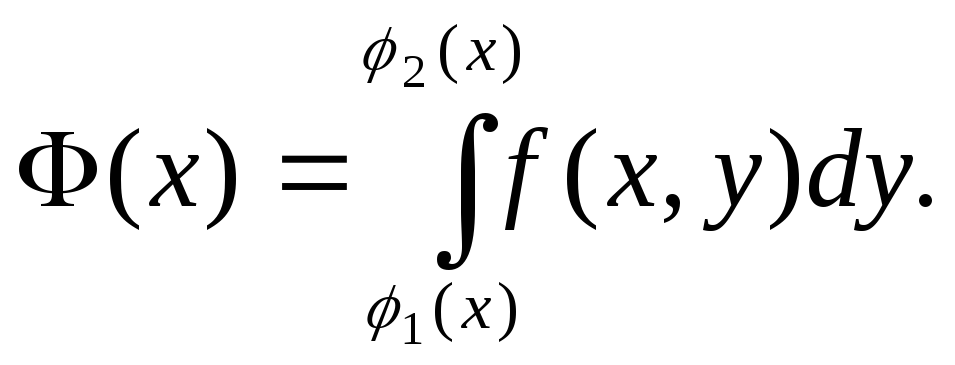
Полученную
функцию проинтегрируем по хв
пределах отадоb.
В результате получим число![]()
Докажем важное свойство двукратного интеграла.
Теорема 8.1. Если областьD, правильная в направлении Оу, разбита на две областиD1иD2прямой, параллельной оси Оуили оси Ох, то двукратный интеграл по областиD будет равен сумме таких же интегралов по областям D1иD2:
![]() .
(8.2)
.
(8.2)
Доказательство.
а) Пусть прямая х = с разбиваетD на D1и D2, правильные в направлении Оу. Тогда

 +
+
+
б) Пусть прямая y = h разбиваетDна правильные в направлении Оуобласти D1и D2(рис.2). Обозначим черезM1(a1,h) иM2(b1,h) точки пересечения прямойy = h с гра-ницейLобластиD.

y ОбластьD1ограничена непрерывными линиями
 y=φ2(x)
1) y = φ1(x);
y=φ2(x)
1) y = φ1(x);


 D22) кривойА1М1М2В,
уравнение которой запишем
D22) кривойА1М1М2В,
уравнение которой запишем
 h M1M2
y = φ1*(x),
гдеφ1*(х) = φ2(х)
приа≤ х ≤ а1и
h M1M2
y = φ1*(x),
гдеφ1*(х) = φ2(х)
приа≤ х ≤ а1и

 A1D1Bb1≤ x ≤ b,φ1*(х) =hпри а1≤ х ≤ b1;
A1D1Bb1≤ x ≤ b,φ1*(х) =hпри а1≤ х ≤ b1;
3) прямыми x = a,x = b.
Область D2ограничена линиямиy = φ1*(x),
A у = φ2(х), а1≤ х ≤ b1.
y=φ1(x) Применим к внутреннему интегралу теорему о
разбиении промежутка интегрирования:
O a a1 b1 b
Рис.2.

+

Представим второй из полученных интегралов в виде суммы:

 +
+ +
+ .
.
Поскольку φ1*(х) = φ2(х) приа≤ х ≤ а1иb1≤ x ≤ b, первый и третий из полученных интегралов тождественно равны нулю. Следовательно,
ID
= 
 ,
то есть
,
то есть![]() .
.
Следствие. Таким же образом можно разбить область Dна любое число правильных областей. При этом двукратный интеграл по областиDбудет равен сумме интегралов по частичным областям.
Замечание 1. Используя теорему 8.1 и теоремы о среднем для определенного интеграла, можно доказать, что для двукратного интеграла справедливы соотношения:
![]()
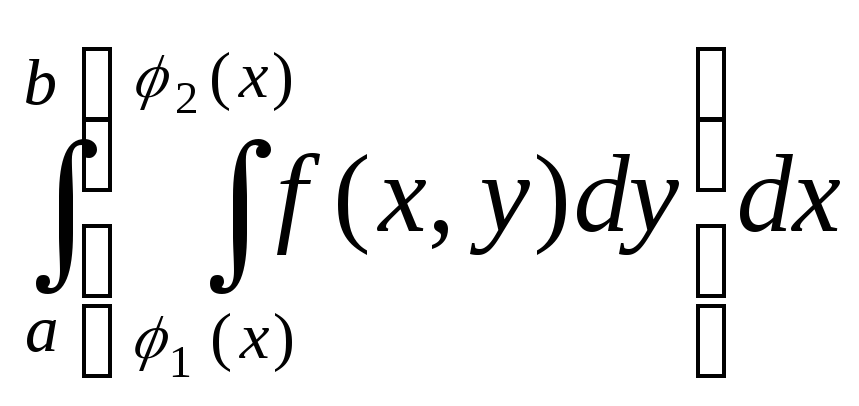
![]() (8.3)
(8.3)
где тиМ– соответственно наименьшее и наибольшее значение функцииf(x, y) в областиD, а S – площадь этой области, и
ID = f(P)S, (8.4)
где Р– точка, принадлежащая областиD .
Замечание 2. Более употребительной формой записи двукратного интеграла является
 =
= (8.5)
(8.5)
Теорема 8.2. Двойной интеграл от непрерывной функцииf(x, y) по правильной областиD равен двукратному интегралу от этой функции по данной области, то есть
![]()
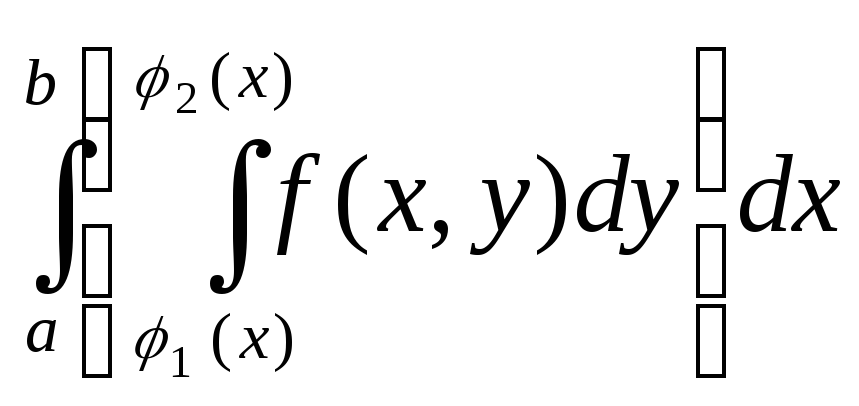 .
(8.6)
.
(8.6)
Доказательство.
Разобьем область Dпрямыми, параллельными координатным осям, напправильных (в основном прямоугольных) областей ΔS1, ΔS2,…, ΔSn. Тогда по теореме 8.1
![]() .
.
Из (8.4) получим:
![]() ,
где справа стоит интегральная сумма,
предел которой равен двойному интегралу
отfпо областиD,
а слева – постоянное числоID. Переходя к пределу при
,
где справа стоит интегральная сумма,
предел которой равен двойному интегралу
отfпо областиD,
а слева – постоянное числоID. Переходя к пределу при![]() ,
получим равенство (8.6).
,
получим равенство (8.6).
Пример.
В

 ычислим
двойной интеграл от функцииz
= x + y
по области, представляющей собой
треугольник с вершинами в точках (0,0),
(0,1) и (1,0) (рис.3).
ычислим
двойной интеграл от функцииz
= x + y
по области, представляющей собой
треугольник с вершинами в точках (0,0),
(0,1) и (1,0) (рис.3).
у Здесьа = 0,b= 1,φ1(x) = 0, φ2(x) = 1 –x.
Тогда
![]()
1 D
![]()
O 1
x
![]()
Рис.3.
