ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

ИНСТИТУТ КОСМИЧЕСКИХ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Теория вероятностей и математическая статистика

Типовой расчет

Вариант 8

Выполнил: Ермолин Павел

Группа КИ10-07

Проверил: Шлёпкин А.К.

Красноярск

2011

Задача 1

Число возможных способов упорядочить множество чисел

Событие A – при упорядочивание множества чисел каждое четное число имеет четный номер среди множества nчетных чисел и n нечетных чисел.

Число способов упорядочить множество чисел благоприятствующие наступлению события А, равно

По определению вероятности

Ответ: вероятность того что при упорядочивании множества чисел каждое четное число имеет четный номер, равна

Задача 2

Определить вероятность безотказной работы за время Т электрической цепи, состоящей из пяти независимо работающих элементов. Вероятности отказов элементов за время Т заданы таблицей.

p	0.1	0.2	0.3	0.4	0.5

Решение:

Пусть событие ={выход из строя элемента }, тогда .

Событие Е – цепь вышла из строя, тогда 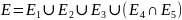. Используя теоремы сложения и умножения вероятностей, а также условия независимости события получаем, что:

0.1+0.2+0.3+0.4*0.5-0.1*0.2-0.1*0.3-0.1*0.4*0.5-0.2*0.3-0.2*0.4*0.5-0.3*0.4*0.5+0.1*0.2*0.3+0.2*0.3*0.4*0.5+0.1*0.3*0.4*0.5+0.1*0.2*0.4*0.5=0.578

Тогда вероятность безотказной работы 1-P(E)=1- =0.422

Ответ: 0.422

Задача 3

Игра между А и В ведется на следующих условиях: первый ход всегда делает А, он может выиграть с вероятностью , если А не выигрывает, то ход делает В и может выиграть в вероятностью . Если В не выигрывает, то А делает второй ход, который может привести к выигрышу с вероятностью . Если А вторым ходом проигрывает, то победителем считается В. Найти вероятность выигрыша для А и В.

Дано:

Решение: Введем обозначения:

Событие А₁ – игрок А выиграл с первого раза

Событие – игрок А не выиграл с первого раза

Событие А₂ – игрок А выиграл со второго раза

Событие – игрок А не выиграл со второго раза

Событие B₁ – игрок B выиграл с первого раза

Событие – игрок B не выиграл с первого раза

Событие C – выиграл игрок А

Событие D – Выиграл игрок В

Выразим события С, D через события А₁, , А₂, , B₁, :

C=

Тогда

Ответ: Вероятность выигрыша для игрока А равна 0,181, а для игрока B–0,819

Задача 4

На складе готовой продукции находитсяn=9изделий, среди которых k=6 высшего качества. Наудачу выбирают m=3 изделий. Найти вероятность того, что среди них l=1 изделий высшего качества.

Решение

Событие А- среди выбранных 3 изделий оказалось высшего качества. Число N всех возможных способов выбора 3 изделий из 9 (общее число исходов) равно числу сочетаний (без повторения элементов) из n элементов по m:

Число M способов выбора 3 изделий из 9, благоприятствующих наступлению события А равно:

Тогда по определению вероятность события А равна:

Ответ: Вероятность того, что среди выбранных 3 изделий оказалось 1 высшего качества равна 0,2143

Задача 5

На складе хранится изделий, изготовленных на заводе 1, изделий – на заводе 2, изделий - на заводе 3. Вероятность того, что деталь, изготовленная на заводе1, высшего качества равна . Для деталей изготовленных на заводах 2 и 3, эти вероятности равны . Найти вероятность того, что при проверке наудачу взятая деталь окажется высшего качества. Какова вероятность того, что она была изготовлена на заводе 2?

Дано: , , , , ;

Решение:

Событие А при проверке наудачу взятая деталь оказалась высшего качества. Это событие может произойти вместе с одной из гипотез , образующих полную группу попарно не совместимых событий:

- наудачу взятая деталь со склада изготовлена на заводе 1;

- наудачу взятая деталь со склада изготовлена на заводе 2;

- наудачу взятая деталь со склада изготовлена на заводе 3.

Найдем вероятности гипотез , следовательно

Проверка: следовательно, вероятности гипотез определены верно.

Вычислим условные вероятности i=1,2,3 того, что наудачу взятая деталь оказалась высшего качества при условии, что она изготовлена на заводеI.

По формуле полной вероятности : имеем

Определим теперь вероятность того, что наудачу взятая деталь, оказавшаяся высшего качества, была изготовлена на заводе 2.

Применим формулу Байеса: ,

Таким образом, ;

Ответ: Вероятность того, что при проверке наудачу взятая деталь окажется высшего качества, равна 0,804, а вероятность того, что она была изготовлена на заводе 2, равна 0,31343