
- •Проекція. Ортогональна система координат. Лівостороння, правостороння системи координат.
- •Радіус-вектор. Властивості радіус-вектора. Перехід від координат точки до радіус-вектора.
- •Рівняння площини у просторі. Проекція радіус-вектора на інший радіус-вектор
- •Математичні основи комп’ютерної графіки. Переміщння. Маштабування. Обертання
- •Представлення об’єктів у тривимірному просторі. Функціональні моделі. Воксельна модель. Полігональні моделі.
- •Типи проекцій. Ізометрична проекція. Аксонометрична проекція.
- •Складові вікна програми 3ds Max. Сцена в 3ds Max. Модифікатори 3dsMax.
- •Об’єкти в 3ds Max. Робота з кольором. Rgb-кольор. Hsl / hsv-властивості.
- •Основи сплайнового моделювання. Вершина. Сегмент. Сплайни. Створення сплайнів. Типи вершин та їх призначення.
- •Полігональне моделювання. Геометрична іерархія підоб’єктів.
- •Метод бікубічних раціональних в-сплайнів. Nurbs-поверхні та їх типи.
- •Матеріали. Основні способи роботи з матеріалами. Матеріали. Потік даних при роботі з матеріалами
- •Освітлення. Типи джерел світла. Приклади застосування. Освітлення. Спрямоване джерело світла Spot. Приклади застосування.
- •Освітлення. Типи джерел світла. Приклади застосування. Освітлення. Спрямоване джерело світла Direct. Приклади застосування.
- •Освітлення. Параметри джерел світла. Принцип трикутного освітлення одиночного об’єкта
- •Камери. Перспектива. Правила розташування камери. Візуалізація. Ефекти візуалізації. Приклади.
- •Інтерфейс OpenGl. Бібліотеки OpenGl
- •Організація бібліотеки OpenGl. Бібліотека динамічної компоновки
- •Синтаксис команд та констант OpenGl. Привести приклади.
- •Команди управління вікном в OpenGl. Привести приклад програми
- •Використання операторних дужок в OpenGl. Обмеження. Привести приклад програми
- •Функції бібліотеки glut/ Чому вони формально не належать OpenGl? Привести приклад програми.
- •Що можно сказати про кількість і тип параметрів функцій glColor4ub(); glVertex3fv(); glVertex2i();
- •Графічне середовище OpenGl. Характерні особливості OpenGl.
- •Графічне середовище OpenGl у чому полягає стабільність, надійність OpenGl.
Проекція. Ортогональна система координат. Лівостороння, правостороння системи координат.
П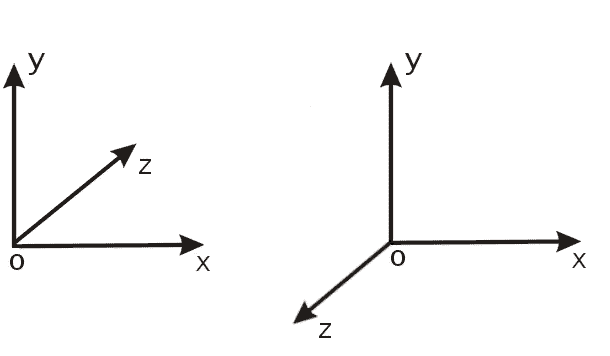 роекцией
точки на координатную ось называется
точка пересечения плоскости, проходящей
через заданную точку и параллельной
плоскости, образованной двумя другими
осями координат.
роекцией
точки на координатную ось называется
точка пересечения плоскости, проходящей
через заданную точку и параллельной
плоскости, образованной двумя другими
осями координат.
Система координат, в которой оси расположены взаимно перпендикулярно, называется ортогональной (взаимное расположение может быть двух видов: левосторонним и правосторонним).
Если посмотреть
из положительной полуоси
![]() в направлении начала координат, то для
совмещения положительной полуоси
в направлении начала координат, то для
совмещения положительной полуоси
![]() с положительной полуосью
с положительной полуосью
![]() необходимо повернуть
относительно начала координат против
часовой стрелки – в этом случае имеем
правую систему координат; если же поворот
производится по часовой стрелке – то
система координат левая
и наоборот.
необходимо повернуть
относительно начала координат против
часовой стрелки – в этом случае имеем
правую систему координат; если же поворот
производится по часовой стрелке – то
система координат левая
и наоборот.
Радіус-вектор. Властивості радіус-вектора. Перехід від координат точки до радіус-вектора.
Декартовы координаты
точек позволяют описывать дополнительные
математические конструкции,
для этого применяют
радиус-векторы. Радиус-векторы обладают
всеми свойствами векторов, но имеют
одну особенность: начало радиус-вектора
находится всегда в начале координат, а
конец радиус-вектора лежит в некоторой
точке пространства. Это свойство
радиус-векторов позволяет поставить
во взаимно однозначное соответствие
им радиус-векторы. Формально это
соответствие запишем в следующем виде.
Пусть точка
![]() имеет координаты
имеет координаты
![]() ,
то есть
,
то есть
![]() ,
и
,
и
![]() –
радиус-вектор, конец которого находится
в точке
,
где
–
радиус-вектор, конец которого находится
в точке
,
где
![]() –
тройка единичных базисных векторов,
или просто нормированный базис. Тогда
точке
взаимно однозначно соответствует
радиус-вектор
–
тройка единичных базисных векторов,
или просто нормированный базис. Тогда
точке
взаимно однозначно соответствует
радиус-вектор
![]() ,
или
,
или
![]() .
Таким образом, можно легко переходить
от координат точек к радиус-векторам и
обратно.
.
Таким образом, можно легко переходить
от координат точек к радиус-векторам и
обратно.
Рівняння площини у просторі. Проекція радіус-вектора на інший радіус-вектор
![]() - уравнение
плоскости.
- уравнение
плоскости.
Иногда бывает необходимо вычислить длину проекции радиус-вектора на другой радиус-вектор.
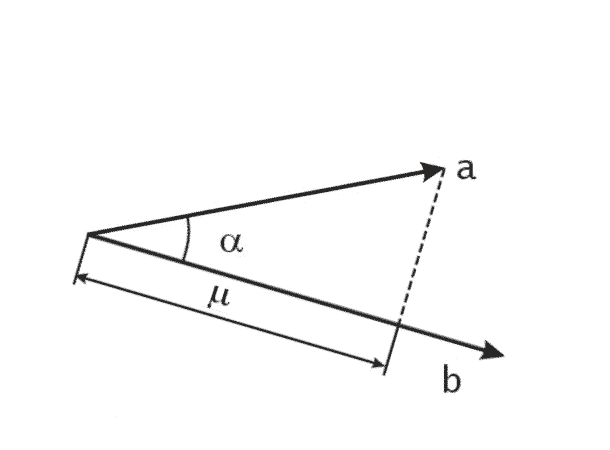
Искомая
длина проекции
![]() =
=![]() =
=![]() .
.
Математичні основи комп’ютерної графіки. Переміщння. Маштабування. Обертання
Математические основы КГ: перемещение, масштабирование и вращение.
Перемещение-это операция, в результате которой точка переходит из одного местоположения в другое. Для перемещения точки в новое положение необходимо к ее координатам сложить некие числа, которые являются координатами вектора перемещения.
Масштабирование-расположение объектов вширь соответствующих осей координат от начала координат. Эта операция используется к каждой точке объекта, поэтому можно говорить о масштабировании точки. Оно достигается умножением координаты точек на некую константу.
Вращение-это процесс в плоскости, при котором точку перемещают по дуге круга, центр которой находится в начале координат.
Представлення об’єктів у тривимірному просторі. Функціональні моделі. Воксельна модель. Полігональні моделі.
К способам представления объектов относят:
Функциональные модели – основной примитив это поверхность другого порядка. Она определяется непрерывной функцией f(x,y,z)>=0. То есть поверхность замкнута подмножеством Е.
Воксельные – представление объекта в виде 3х мерного массива объемных или кубических элементов. Полная прозрачность вокселя значит пустоту в соответствующей точке объекта. Чем > вокселей и < их размер, тем точнее моделирование.
Полигональные – основными элементами есть вершина, а остальные производные – линия, полилиния, полигон, полигональная поверхность.
