6. Математическое ожидание случайной величины.

Математическое ожидание дискретной случайно величины Х принимающей конечное множество значение с законом распределения:

P(X= )=

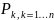
, называется сумма произведений ее значений на их соответствующие вероятности.

Математической ожидание дискретной случайной величины Х равно среднему арифметическому всех ее возможных значений , вследствие этого, математическое ожидание случайной величины называют средним значением.

Математическое ожидание дискретной случайной величины, принимающей бесконечную последовательность значений с законом распределения

P(X= )=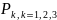 , где сумма определяется формулой

M(X)= , если этот ряд сходится абсолютно.

Математическое ожидание непрерывной случайной величины Х , все значения которой принадлежат отрезку (α; , а p(x) ее плотность вероятности , определяется по формуле:

M(X)=

Если все значения непрерывной случайной величины Х принадлежат бесконечному промежутку (-∞;+∞), а p(x) ее плотность вероятности, то математическое ожидание определяется формулой :

M(X)= , если этот несобственный интеграл сходится абсолютно.

Свойства Математического ожидания:

1)Значение математического ожидания случайной величины Х заключено между ее наименьшим и наибольшим значением :

a

2)Математическое ожидание постоянной величины равно этой постоянной:

M(C)=C

3) Постоянный множитель можно вынести за знак математического ожидания

М(СХ)=СМ(Х)

4)Математическое ожидание суммы двух случайных величин , равно сумме их математических ожиданий:

M(X+Y)=M(X)+M(Y)

5)Математическое ожидание разности двух случайных величин равно разности их математических ожиданий

М(X-Y)=M(X)-M(Y)

6)Математическое ожидание произведений двух независимых случайных величин равно произведению математических ожиданий этих величин.

M(XY)=M(X)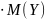

Распространяется на n независимых случайных величин.

6. Дисперсия случайной величины и ее свойства.

Дисперсией случайной величины Х называется математическое ожидание квадрата ее отклонения :

D(X)=M

Из определения и свойств математического ожидания следует, что дисперсия любой случайной величины неотрицательна

D(X)≥0

Для вычисления дисперсии применяется формула

D(X)=M(

Свойства дисперсии:

1. Дисперсия постоянной величины равна 0.

D(C)=0

2. Постоянный множитель можно вынести за знак дисперсии, при этом возведя его в квадрат

D(CX)=

3. Дисперсия суммы двух независимых случайных величин

D(X+Y)=D(X)+D(Y)

4. Дисперсия непрерывной случайной величиины Х, все значения которой принадлежат отрезку [α;β] определяется формулой :

D(X)=

5. Дисперсию можно вычислить по формуле

D(X) =

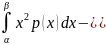
6. Дисперсия непрерывной случайной величины X все значения которой принадлежат интервалу (- вычисляется по формуле :

D(X)=

Если этот несобственный интеграл сходится абсолютно

7. Средним квадратическим отклонением случайной величины Х называют корень из ее дисперсии.

6. Среднее квадратическое отклонение

Разность X-M(X)называется отклонением случайной величины Х от ее математического ожидания M(X). Математическое ожидание отклонения равно 0.

M(X-M(X))=0

Средним квадратическим отклонение случайной величины Х называется корень из ее дисперсии:

6. Формула Бернули.

Производятся испытания в каждом из которых может появиться события А или событие не А, если вероятность события А в одном испытании не зависит от появления его в любом другом , то испытания называются независимыми относительно события А. Будем считать, что испытания происходят в одинаковых условиях, и вероятность появления события А в каждом испытании одна и та же.

Обозначим эту вероятность через p, а вероятность не А через q. P+q=1. Вероятность того, что в серии из n независимых испытаний события А появится ровно e раз и не появится

(n-k) раз обозначим через

-Формула Бернули