• Момент импульса твердого тела. Закон сохранения момента импульса.

Момент импульса материальной точки относительно точки O определяется векторным произведением , где   — радиус-вектор, проведенный из точки O,   — импульс материальной точки. Момент импульса материальной точки относительно неподвижной оси    равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса    не зависит от положения точки O на оси z.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что  , получим .

Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):  .

Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело: .

Гармонические колебания. Скорость, ускорение. Сила в колебательном движении.

Г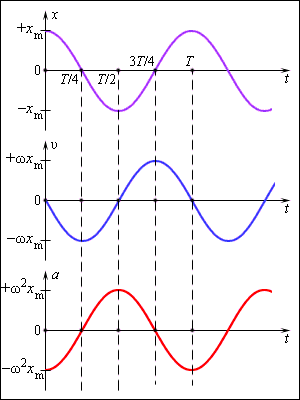 армоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом: x(t) = Asin(ωt + φ)илиx(t) = Acos(ωt + φ)

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание). Условия возникновения свободных колебаний:

а) при выведении тела из положения равновесия в системе должна возникнуть сила, стремящаяся вернуть его в положение равновесия;

б) силы трения в системе должны быть достаточно малы.

• Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (т.е. чтобы зависимость от времени этой силы была синусоидальной).

• На рис. 2.1.4 приведены графики координаты, скорости и ускорения тела, совершающего гармонические колебания.

• Энергия гармонического колебания.

Полная механическая энергия тела не изменяется при колебаниях:    2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника.  3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на p (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.

 При колебаниях, совершающихся под действием потенциальных (консервативных) сил, происходит переход кинетической энергии в потенциальную и наоборот, но их сумма в любой момент времени постоянна.

• Сложение гармонических колебаний, направленных вдоль одной прямой. Биения.

Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями. Строго говоря, это уже не гармонические колебания.

• Сложение взаимно-перпендикулярных колебаний.

Рассмотрим сложение взаимно перпендикулярных колебаний на примере механических колебаний. Допустим, что материальная точка может совершать колебания как вдоль оси Оx, так и вдоль перпендикулярной к ней оси Оy. Если возбудить оба колебания, материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.

Затухающие колебания. Логарифмический декремент затухания

ЗАТУХАЮЩИЕ КОЛЕБАНИЯ - колебания с постоянно убывающей со временем амплитудой.Свободные колебания реальных систем всегда затухают. Затухание обусловлено в основном трением (механические системы) и сопротивлением ( в электромагнитных колебательных контурах).Колебательная система называется линейной, если её свойства не меняются при колебаниях, то есть такие параметры, как сила тяжести, упругость пружины, сопротивление, емкость, индуктивность не зависят ни от смещения, ни от скорости, ни от ускорения колеблющейся величины. В дальнейшем мы будем рассматривать только линейные системы. Уравнения затухающих колебанийПолучим дифференциальное уравнение свободных затухающих колебаний на примере реального пружинного маятника, совершающего колебания в среде с сопротивлением (простейший случай - трение о воздух). Пусть масса маятника m, коэффициент упругости пружины k, сила сопротивления, действующая на маятник, F = - bv, v - скорость маятника, b - коэффициент сопротивления среды, в которой находится маятник. Так как мы рассматриваем только линейные системы, b = const, k = const. x - смещение маятника от положения равновесия.Второй закон Ньютона в нашем случае запишется так:

Это уравнение и есть дифференциальное уравнение свободных затухающих колебаний пружинного маятника. Его, однако, принято записывать в следующем, так называемомканоническом виде:

   - коэффициент затухания,     - собственная частота свободных (незатухающих) колебаний пружинного маятника, то, что раньше мы обозначали просто w.Уравнение затухающих колебаний в таком (каноническом) виде описывает затухающие колебания всех линейных систем; конкретная колебательная система отличается только выражениями для b и j₀.логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в eраз.

Если χ = 0,01, то N = 100.