• Эффект Джоуля-Томпсона.

Если идеальный газ адиабатически расширяется и совершает при этом работу, то он охлаждается, так как работа в данном случае совершается за счет его внутренней энергии. Подобный процесс, но с реальным газом — адиабатическое расширение реального газа с совершением внешними силами положительной работы — осуществили английские физики Дж. Джоуль (1818—1889) и У. Томсон (лорд Кельвин, 1824—1907).

Рассмотрим эффект Джоуля — Томсона. Так как расширение газа происходит без теплообмена с окружающей средой (адиабатически), то на основании первого начала термодинамики

                                                                      (64.1)

Внешняя работа, совершаемая газом, состоит из положительной работы при движении поршня 2 (А₂=р₂V₂) и отрицательной при движении поршня 1 (A₁=p₁V₁), т. е. dA=A₂—A₁. Подставляя выражения для работ в формулу (64.1), получаем

                                                  (64.2)

Таким образом, в опыте Джоуля — Томсона сохраняется (остается неизменной) величина U+pV. Она является функцией состояния и называется энтальпией.

Ради простоты рассмотрим 1 моль газа. Подставляя в формулу (64.2) выражение (63.3) и рассчитанные из уравнения Ван-дер-Ваальса (61.2) значения p₁V₂  ир₂V₂ (символ «m» опять опускаем) и производя элементарные преобразования, получаем

                                 (64.3)

1) а » 0 — не учитываем силы притяжения между молекулами, а учитываем лишь размеры самих молекул. Тогда

т. е. газ в данном случае нагревается;

2) b » 0 — не учитываем размеров молекул, а учитываем лишь силы притяжения между молекулами. Тогда

т. е. газ в данном случае охлаждается;

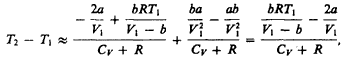Изменение температуры реального газа в результате его адиабатического расширения, или, как говорят, адиабатического дросселирования — медленного прохождения газа под действием перепада давления сквозь дроссель (например, пористую перегородку), называется эффектом Джоуля—Томсона. Эффект Джоуля — Томсона принято называть положительным, если газ в процессе дросселирования охлаждается (DT<0), и отрицательным, если газ нагревается (DT > 0).

В зависимости от условий дросселирования для одного и того же газа эффект Джоуля — Томсона может быть как положительным, так и отрицательным. Температура, при которой (для данного давления) происходит изменение знака эффекта Джоуля — Томсона, называется температурой инверсии. Ее зависимость от объема получим, приравняв выражение (64.4) нулю:

                                         

• Электростатическое поле. Закон Кулона.

Опыт с электризацией пластин доказывает, что при электризации трением происходит перераспределение имеющихся зарядов между телами, нейтральными в первый момент. Небольшая часть электронов переходит с одного тела на другое. При этом новые частицы не возникают, а существовавшие ранее не исчезают. При электризации тел выполняется закон сохранения электрического заряда. Этот закон для замкнутой системы. В замкнутой системе алгебраическая сумма зарядов всех частиц остается неизменной. Если заряды частиц обозначить через q1, q2 и т.д., то q1, +q2 +q3 +…+qn = constСправедливость закона сохранения заряда подтверждают наблюдения над огромным числом превращений элементарных частиц. Этот закон выражает одно из самых фундаментальных свойств электрического заряда. Причина сохранения заряда до сих пор неизвестна.Закон Кулона. Опыты Кулона привели к установлению закона поразительно напоминающего закон всемирного тяготения. Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей заряда и обратно пропорциональна квадрату расстояние между ними. Эту силу называют кулоновской.Если обозначить модули зарядов через |q1| и |q2|, а расстояние между нимичерез r, то закон Кулона можно записать в следующей форме:где k — коэффициент пропорциональности, численно равный силе взаимодействия единичных зарядов на расстоянии, равном единице длины. Его значение зависит от выбора системы единиц.

Закон Кулона: сила взаимодействия двух точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.  Эта сила называется кулоновской. Она направлена вдоль прямой, соединяющей тела, то есть является центральной. Кулоновская сила может быть как силой притяжения, так и силой отталкивания; положительной считают силу отталкивания. Поэтому закон Кулона можно записать в векторном виде:  Напряженность поля. Принцип суперпозиции полей. Электрическое смещение.

Напряженность электрического поля. Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля.

E = F / q _пр.

Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд q_пр, помещенный в рассматриваемую точку поля, к величине этого заряда.

Понятие «пробный заряд» предполагает, что этот заряд не участвует в создании электрического поля и так мал, что не искажает его, т. е. не вызывает перераспределения в пространстве зарядов, создающих рассматриваемое поле. В системе СИ единицей напряженности служит 1 В / м, что эквивалентно 1 Н / Кл.

Напряженность поля точечного заряда. Используя закон Кулона (1.1) найдем выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда:

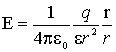   (1.2)

В этой формуле r – радиус-вектор, соединяющий заряды q и q_пр. Из (1.2) следует, что напряжённость E поля точечного заряда q во всех точках поля направлена радиально от заряда при q > 0 и к заряду при q < 0.

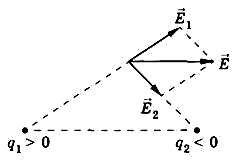
Принцип суперпозиции. Напряжённость поля, создаваемого системой неподвижных точечных зарядов q₁, q₂, q₃, ¼, q_n, равна векторной сумме напряжённостей электрических полей, создаваемых каждым из этих зарядов в отдельности:                                           

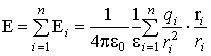
где r_i – расстояние между зарядом q_i и рассматриваемой точкой поля.

Принцип суперпозиции, позволяет рассчитывать не только напряжённость поля системы точечных зарядов, но и напряженность поля в системах, где имеет место непрерывное распределение заряда. Заряд тела можно представить как сумму элементарных точечных зарядов dq.

При этом, если заряд распределен с линейной плотностью t, то dq = t dl; если заряд распределен с поверхностной плотностью s, то dq =  dl и dq = r dl, если заряд распределен с объёмной плотностью r.

Графическое изображение электрического поля. Метод графического изображения электрического поля был предложен английским физиком Майклом Фарадеем. Суть метода заключается в том, что на чертеже изображаются непрерывные линии, которые называют линиями напряженности, или силовыми линиями.

Правило построения линий напряженности заключается в том, что касательные к ним в каждой точке чертежа совпадают с направлением вектора напряженности поля в изображаемой точке.

Таким образом, силовые линии имеют то же направление, что и напряжённость поля и не пересекаются, так как в каждой точке электрического поля вектор E имеет лишь одно направление.

С помощью силовых линий можно дать количественную характеристику напряжённости электрического поля. Для этого густота, или плотность, силовых линий выбирается пропорционально модулю вектора напряженности. Плотность силовых линий определяется как число линий, пронизывающих единичную поверхность в направлении, перпендикулярном к этой поверхности.

Изображение силовых линий позволяет получать картину поля, которая наглядно показывает, чему равна напряженность в разных частях поля и как она изменяется в пространстве.