ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ИРКУТСКИЙ ЭНЕРГЕТИЧЕСКИЙ КОЛЛЕДЖ
РАСЧЕТНО-ГРАФИЧЕСКая РАБОТа
ПО ПРЕДМЕТУ
«ТЕХНИЧЕСКАЯ МЕХАНИКА»
ВАРИАНТ 10
Выполнил: студент гр. 2РЗ1
Грудинин В.Н.
Проверил: преподаватель
Семенюк Л.А.
-
Работа №
1
2
3
4
5
6
7
Оценка
Иркутск 2011 Практическая работа № 1 Определение равнодействующей плоской системы сходящихся сил
Задания:
Заданы модули сил F1, F2, F3, пересекающихся в одной точке, и направление этих сил – углы α1, α2, α3 относительно оси Х (рис. 1.1 и табл. 1.1) .
Цель работы – произвести графическое и аналитическое исследование плоской системы сходящихся сил, выявить уравновешена ли заданная система сил.
Дано:
F1
= 7 Н, α =
150
,
F2
= 8Н, α2
= 45
,
F3
= 9H,
α3
= 330
1. Графическое определение равнодействующей.
Выбираем масштаб сил – μF = 1Н/ см
Модуль равнодействующей
-
=
μF
* 1 = 0.1*87,4 = 8,74
Направление
равнодействующей -
= 32,20°
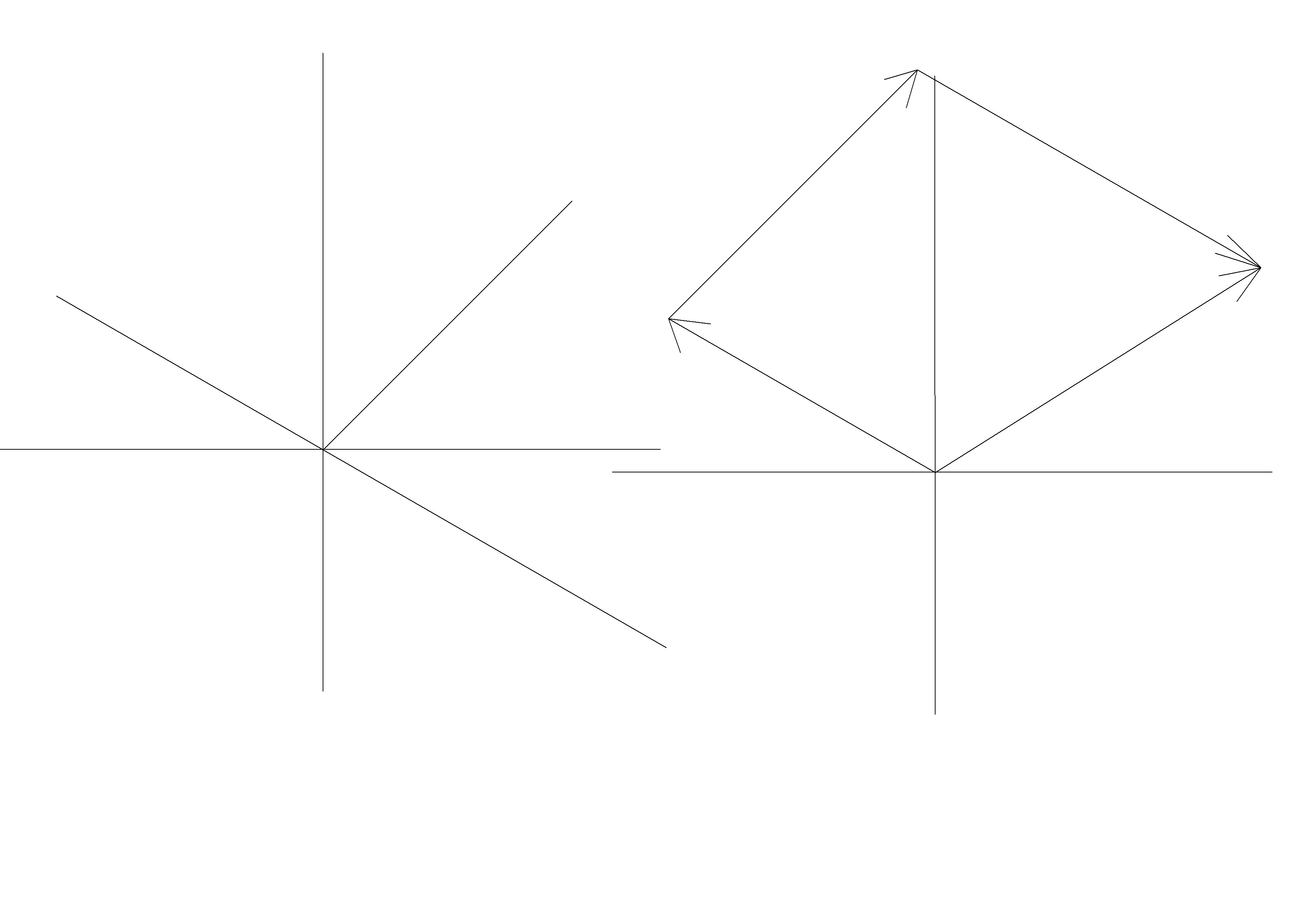
2. Аналитическое определение равнодействующей проекции заданных сил на оси х и у:
F1x = F1* cosα1= 7*cos150° = -6,062177 Н; F1y = F1* sinα1 = 7* sin150° = 3,5 H;
F2x = F2 * cosα2 = 8* cos45° = 5,656854 H; F2y = F2 * sinα2 = 8* sin45° = 5,656854 H;
F3x = F3* cosα3 = 9* cos330° = 7,794228 H ; F3y = F3* sinα3 = 9*sin330° = - 4,5 H;
Проекции равнодействующей:
F∑x = ∑Fix = - 6,062177+5,656854+7,794228=7,388905Н,
F∑y =∑Fiy = 3,5+5,6568-4,5=4,656854Н.
Модуль равнодействующей:
F∑
=
=
=
8.733968 H;
Направление
равнодействующей: α
=
arctg
3. Относительные погрешности
Погрешность вычисления модуля равнодействующей.
*
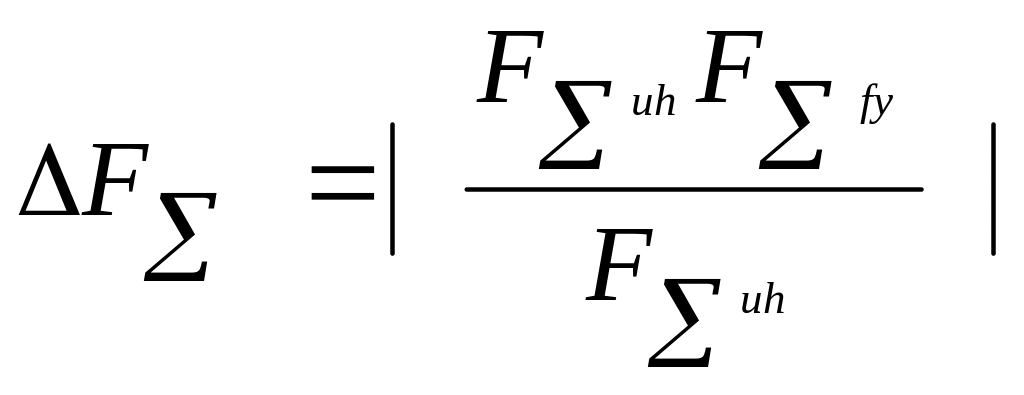100% =
*
100% = 0,069%
Погрешность вычисления направления равнодействующей
*100% =
*100%
= -0,071%
Вывод: система является неуравновешенной.
Модуль равнодействующей
- F∑
= 8,74 Н, направление -
= 32,222°.
Относительные погрешности не превышают 5%.
Вывод 2: Погрешность программы, по которой был начерчен чертёж
не превышает 0,2% (скорее всего программа просто округлила значения до десятых долей)
Контрольные вопросы №1
1. Графическое сложение плоской системы сходящихся сил производят построением силового многоугольника.Порядок сложения векторов т.е НЕ F1 к F2 к F3 и т.д , а например F3 к F1 к F5 Сильно влияет на величину равнодействующей.
2. Равнодействующая направлена из начала координат к концу последнего вектора.
3. Да. Если конец вектора последней силы совпал с началом вектора первой силы, то система уравновешена.
5. Если модуль равнодействующей равен нулю, то система уравновешена.
4.Она определяется
умножением силы на угол
.
Проекция равна нулю если: 1) проекция
ведётся на ось х и угол равен 90 т.е
cos90=0.
2)П проекция ведётся на ось у и угол равен
180 т.е sin180=0.
6. Графический способ определения равнодействующей следует применять, если сил мало и для наглядного изображения, а аналитический для точного расчёта.
7. Чтоб произвести уравновешивание плоской системы сходящихся сил надо наверное вычислить равнодействующую и заменить её век
Практическая работа № 2
Расчётные схемы балок и определение реакции их опор
Задание
Задана горизонтальная двух опорная балка. Балка нагружена активными силами: сосредоточенной F, распределенной силой интенсивностью q и парой сил с моментом М (табл.2.1 и рис 2.6).
Цель работы – построить расчётную схему балки, составить уравнения равновесия балки, определить реакции ее опор и выявить наиболее нагруженную опору.
Дано:
q = 4 H/м, F = 50 H, M = 10 H*м, α = 120°
Преобразование заданных сил:
Fx = F cos α = 50cos 120° = -25, Fy = F sinα = 50 sin120° = 43.3012
Q = q*l = 4*1=4H.
Составим расчётную схему
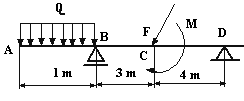
Q М
F
А В
С
D
Уравнения равновесия и определение реакций опор:
а
)
∑Mia
=
0; -Q *AB/2 – Fy
* AC+
RB
*
3 – M = 0;
RB
=
б) ∑MiB =0: - RAy*AB + Q *AB/2 + Fy *AC – M = 0:
RAy
=
в) ∑Fix=0: RAx + Fx =0: RAx= - Fx = 25H.
5.Проверка:
∑Fiy = 0; RAy = Q – Fy + RB = 0; 4 – 43.3012+40.3= 0; 0 = 0
Вывод:
Наиболее нагруженной
является опора В – RB
=-40.3Н. Нагрузка на опору А – RA
=
