
- •Понятие транслятора. Структура транслятора. Фазы трансляции. Основные блоки транслятора.
- •Понятие транслятора. Многопроходная организация взаимодействия блоков транслятора.
- •Понятие транслятора. Однопроходная организация взаимодействия блоков транслятора.
- •Понятие транслятора. Комбинированные взаимодействия блоков транслятора.
- •Способы определения языков. Механизмы порождения и распознавания.
- •Формальные грамматики. Порождающие грамматики Хомского.
- •Конечные автоматы. Детерминированные конечные автоматы.
- •Конечные автоматы. Недетерминированные конечные автоматы.
- •Автоматы с магазинной памятью. Устройство автомата с магазинной памятью.
- •Автоматы с магазинной памятью. Детерминированные и недетерминированные автоматы с магазинной памятью.
- •Машина Тьюринга. Устройство машины Тьюринга. Отличия конечного автомата от машины Тьюринга.
- •Машина Тьюринга. Линейно-ограниченные автоматы.
- •Системы Линденмайера (l-системы). Внутреннее устройство l-систем.
- •Системы автоматической генерации компиляторов. Основные спецификации и идеологии.
- •Системы автоматической генерации компиляторов. Проект Coco/r.
- •Системы автоматической генерации компиляторов. Проект Yacc.
- •Системы автоматической генерации компиляторов. Генерация лексического анализатора.
- •Системы автоматической генерации компиляторов. Генерация синтаксического анализатора.
- •Понятие компилятора. Этапы анализа исходной программы.
- •Понятие компилятора. Лексический анализ.
- •Понятие компилятора. Синтаксический анализ.
- •Понятие компилятора. Семантический анализ.
- •Понятие компилятора. Основные фазы компиляции.
- •Понятие компилятора. Генерация кода. Основные подходы к генерации кода. Понятие целевой машины.
- •Понятие компилятора. Оптимизация кода. Основные источники оптимизации.
Конечные автоматы. Детерминированные конечные автоматы.
Конечный автомат — математическая абстракция, позволяющая описывать пути изменения состояния объекта в зависимости от его текущего состояния и входных данных, при условии, что общее возможное количество состояний конечно.
Детерминированным конечным автоматом (ДКА) называется некоторое виртуальное устройство, распознающее цепочки символов. Она имеет входную ленту, разбитую на клетки, и содержащую некие символы. На входной ленте установлена подвижная головка (входная головка) указывающая состояние автомата (количество состояний конечно). Среди состояний выделяют начальное состояние (состояние на момент запуска) и допускающие состояния (ничем не отличаются от обычных и используются для анализа работы автомата). Автомат также имеет таблицу переходов состояний (рис. 1).
Конечный
автомат М можно представить в виде
пятерки (S, I,
![]() ,
q0, F), где
,
q0, F), где
1) S - множество состояний автомата,
2) I - входной алфавит (каждая клетка входной ленты содержит символ из I),
3) - функцией переходов автомата, отображающая S и I в множество подмножеств множества S,
4) q0 – начальное состояние,
5) F - подмножество в S, называемое множеством допускающих (или заключительных) состояний.
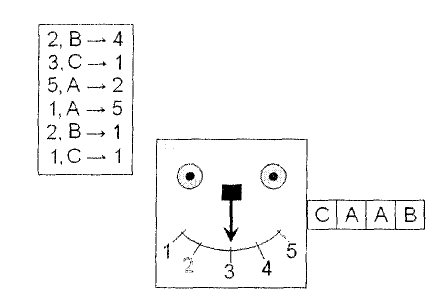
Рис. 1. Конечный автомат.
Автомат считывает очередной входной символ и переходит в новое состояние согласно таблице переходов, затем цикл повторяется. Работа заканчивается, когда вся лента будет обработана.
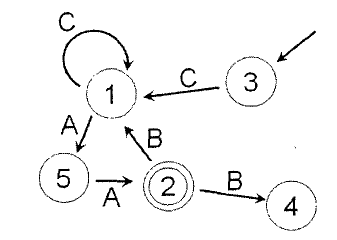
Рис. 2. Представление в виде графа.
Конечные автоматы. Недетерминированные конечные автоматы.
Конечный автомат — математическая абстракция, позволяющая описывать пути изменения состояния объекта в зависимости от его текущего состояния и входных данных, при условии, что общее возможное количество состояний конечно.
Отличие недетерминированного автомата от детерминированного заключается в том, что в нем допускаются противоречащие правила. Для каждого состояния и каждого входного символа недетерминированного конечного автомата
имеет ноль или более вариантов выбора следующего шага. Он может также выбирать, сдвигать ему входную головку при изменении состояния или нет.
Недетерминированным конечным автоматом называется пятерка (S, I, , q0, F), где
1) S - конечное множество состояний;
2) I - алфавит входных символов;
3) - функция переходов, отображающая S и I в множество подмножеств множества S;
4) q0 - начальное состояние устройства управления;
5) F – множество заключительных (допускающих) состояний.
С каждым НКА связан ориентированный граф, естественным образом представляющий функцию переходов этого автомата.
Графом переходов автомата М называют ориентированный граф G = (S,E) с помеченными ребрами. Например на рис.2. изображен граф переходов для некоторого НКА. Заключительное состояние обведено двойной рамкой.

Рис. 3. Граф переходов
Автоматы с магазинной памятью. Устройство автомата с магазинной памятью.
Автомат с магазинной памятью — это конечный автомат, снабженный дополнительным стеком (магазином) для хранения промежуточной информации потенциально бесконечного объема.
Конечное управляющее устройство снабжается дополнительной управляющей головкой, всегда указывающей на верхнюю ячейку магазинной памяти; за один такт работы автомата (преобразователя) управляющая головка может произвести следующие движения:
1) стереть символ из верхней ячейки (при этом все символы, находящиеся на рабочей ленте, перемещаются на одну ячейку вверх);
2) стереть символ из верхней ячейки и записать на рабочую ленту непустую цепочку символов (при этом содержимое
рабочей ленты сдвигается вниз ровно настолько, какова длина
с записываемой цепочки).
МП-автомат
имеет конечное множество внутренних
состояний S
с начальным состоянием s0
и подмножеством F
заключительных
состояний, конечный алфавит входных
сигналов X
и
конечный алфавит магазина Г с маркером
![]() ,
который обозначает дно стека. Функция
переходов
по каждой тройке <текущее
внутреннее состояние, очередной входной
сигнал, верхний символ магазина>
определяет
на очередном шаге функционирования
следующее состояние и цепочку символов
магазинной памяти, записываемых в
магазин вместо прочитанного верхнего
символа (условимся, что цепочка
записывается в стек "хвостом вперед",
т. е. сначала в стек записывается последний
символ цепочки, затем предпоследний и
т.д.). МП-автомат распознает входную
цепочку, если после ее завершения на
входе автомат перейдет в одно из
заключительных состояний и его магазин
будет пустым.
,
который обозначает дно стека. Функция
переходов
по каждой тройке <текущее
внутреннее состояние, очередной входной
сигнал, верхний символ магазина>
определяет
на очередном шаге функционирования
следующее состояние и цепочку символов
магазинной памяти, записываемых в
магазин вместо прочитанного верхнего
символа (условимся, что цепочка
записывается в стек "хвостом вперед",
т. е. сначала в стек записывается последний
символ цепочки, затем предпоследний и
т.д.). МП-автомат распознает входную
цепочку, если после ее завершения на
входе автомат перейдет в одно из
заключительных состояний и его магазин
будет пустым.
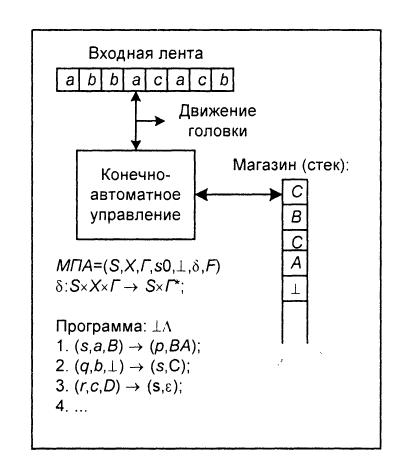
Реализация автоматов с магазинной памятью отличается от конечных автоматов тем, что текущее состояние автомата сильно зависит от любого предыдущего.
