11.Принцип оптимальности Беллмана. Применение принципа при построении оптимальной стратегии управления.

Этот принцип сост-ет основу динамического программирования и формулир-ся след обр.

«Оптимальная стратегия обладает тем свойством, что каково бы не было состояние входа первой стадии х⁽⁰⁾ и управления на ней u⁽¹⁾, последующее управление u⁽²⁾, u⁽³⁾… u⁽ⁿ⁾ составляют оптимальную стратегию отн-но выхода первой стадии x⁽¹⁾, Связанной уравнением состояния с величиной входа x⁽⁰⁾ и управлением u⁽¹⁾».

При применении принципа оптимальности критерий эффективности зависит от х⁽⁰⁾:

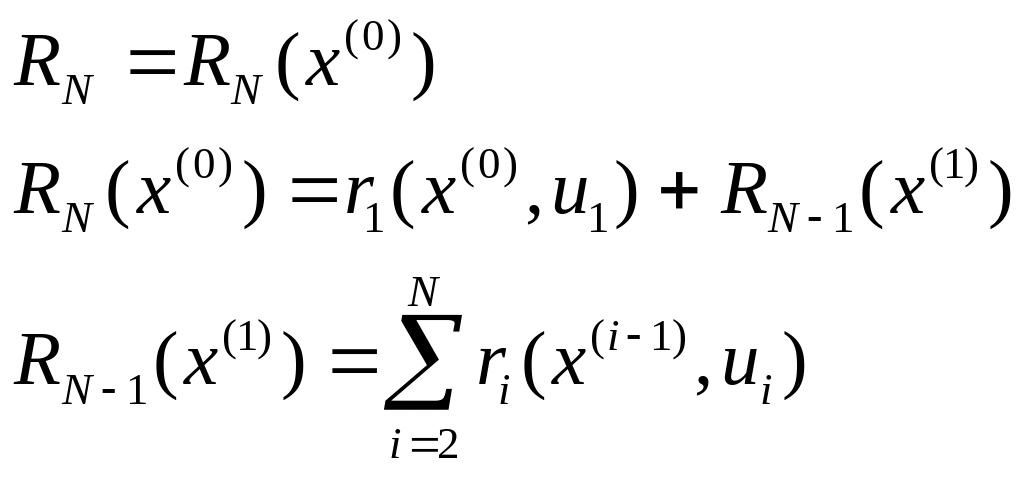( 1)

(2)

(3)

Обозначим через (4).

Перепишем (4) учитывая (2):

(5)

Обозначим максимальное значение:

(6)

Тогда (5) с учетом (6):

Учитывая :

- это реккурентное соотношение является матем. формулировкой принципа оптимальности для дискретных процессов.

12. Синтез оптимального регулятора. Решение задачи принципа максимума.

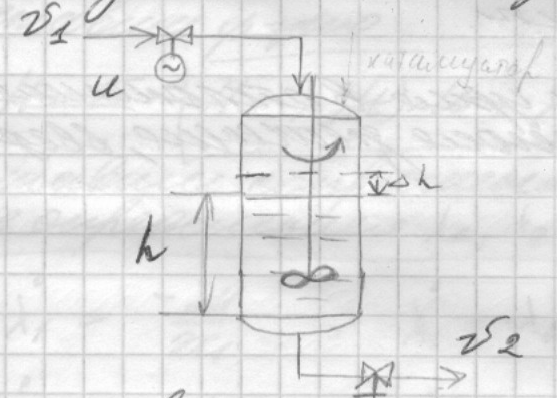
В аппарате необходимо поддерживать на заданном значении уровень жидкости h. Возмущения поступает по линии истока в результате изменения расхода υ_2. В результате изменения расхода υ₂ (например при увеличении) уровень жидкости изменяется (уменьшается). Для поддержания его на заданном значении необходимо увеличить приток жидкости υ₁. Изменение притока жидкости осуществляется с помощью регулирующего органа, привод которого связан с электродвигателем. Расход жидкости υ₁ пропорционален напряжению и знаку приложенного к электродвигателю U. Скорость изменения расхода лин-на зависит от

U: (1) k – коэф. передачи.

Уравнение материального баланса: , S – сечение. x₁=Δυ₁, x₂=SΔh, ξ=Δυ₂, u=kU, x₁, x₂, ξ – отклонение параметров от стационарного состояния. Исходные уравнения:

(4) -u₀≤u≤u₀

Задача: требуется найти такой значение управления u (t`), удовлетворяющей (4) при котором возможно перевести систему (1) из начального состояния (2) в конечное (3) за минимальное время Т. Управление u(t), напряжение электродвигателя может принимать “+”-ое и “-“-oе значение.

H=λ₁(u)+ λ₂(x₁-ξ), , λ₁(t)= - x₂t+C₁, λ₂ (t)=C₂, λ₁(t)=C₁+C₂t,

функция λ₁(T) линейная функция и при изменение времени t, только один раз меняет свой знак . max H достигается при

или U_опт=U₀*sign λ₁ (5)

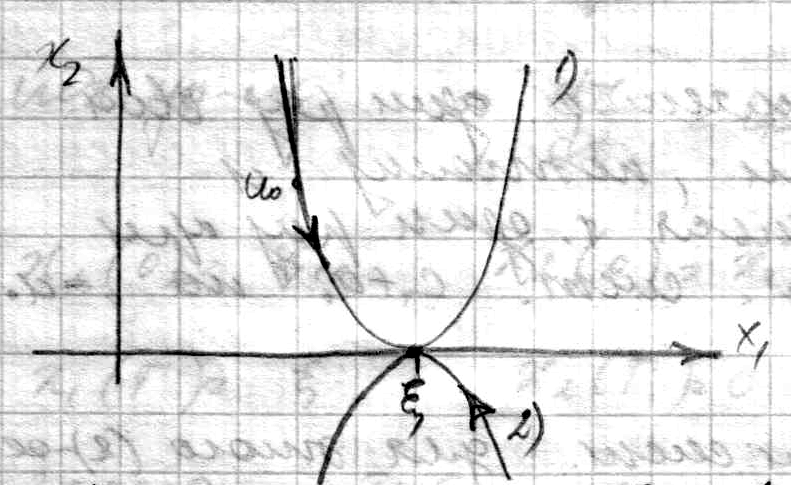
Т.к. функция λ₁(t) меняет свой знак один раз при изменении времени, то управление будет меняться только один раз при переходе из начального состояния системы в конечное или наоборот. Построим фазовый портрет системы, для этого (2)-ое уравнение системы (1) разделим на 1-ое.

уравнение фазовой траектории, где С₂=const интегрирования. Если она проходит ч/з начальную точку заданную (2), то С₂ – определим из этих условий.

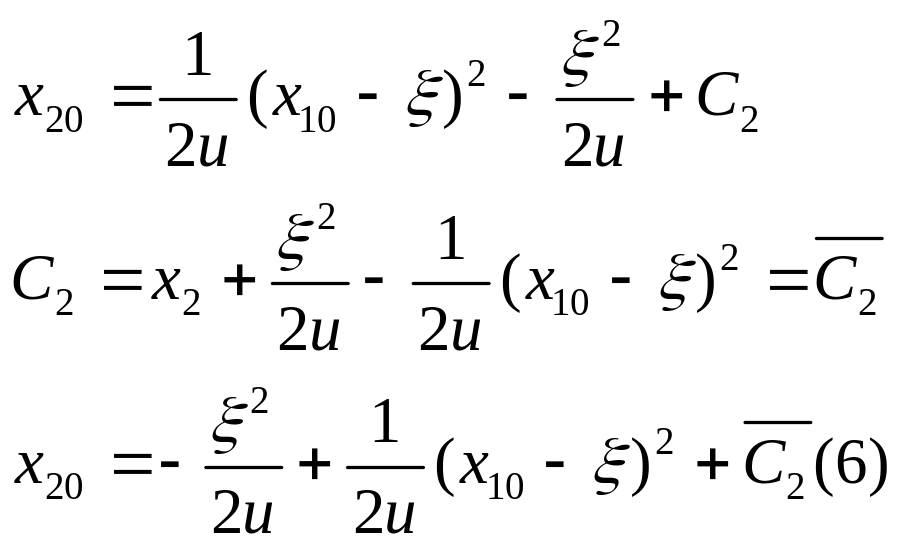
(6) уравнение фазовой траектории ч/з нач. точку. Уравнение фазовой траектории ч/з конечную точку.

, где С₂-определяется из конечных условий (2)

(7) уравнение фазовой траектории ч/з конечную точку.

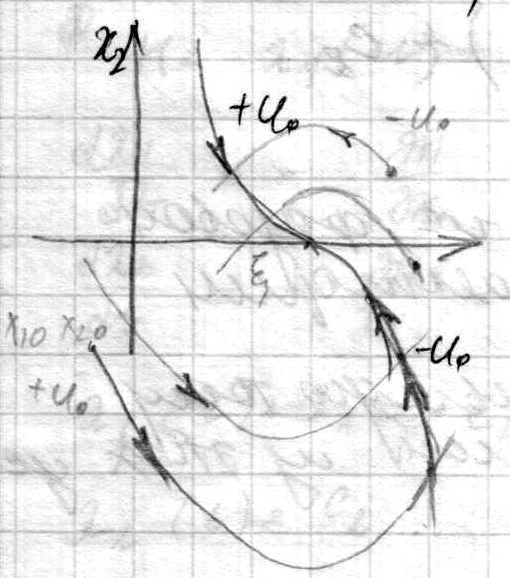
Изобразим уравнение фазовой траектории ч/з конечную точку: u=+u₀, x₂= . При возрастании Т из 1-го уравнения (1) при управлении +u₀ в конечную точку ξ можно попасть проходя по левой ветви параболы.

если u=-u₀, x₂ по правой ветви линии переключения параболы только по этой линии можно попасть в конечную точку.

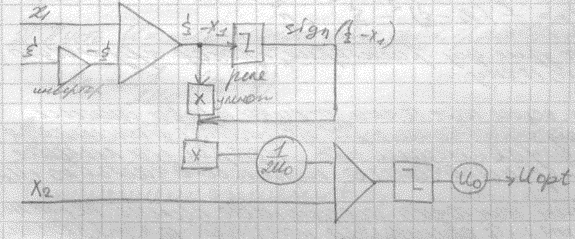
Если начальная точка задана правее линии переключения, то оптимальный закон управления. Чтобы получить u_опт нужно измерить x₁,x₂,ξ, υ₁, υ₂ и уровень h. Для технической реализации можно собрать схему из аналоговых элементов и двух линейных реле реализующих функцию знака