2 1. Свойства f-ии Гамильтона.

На опт. траектории f H непрерывна и пост-на. Не б-м доказ-ть нпрвнть f-ии H, а приведем т-ко нестрогое док-во ее пост-ва на опт траектори. Для этого составим полную произв-ую от f-ии H:

И сп-уя канонич. ф-му ур-я Гамильтона: , подставим знач-я произв-ых от λ и х по T в выр-я для полн. произв-ой.

Получим: =>

На опт траектории, т.е. при u=u₀ f H имеет max. Рас-им 2 усл-я:

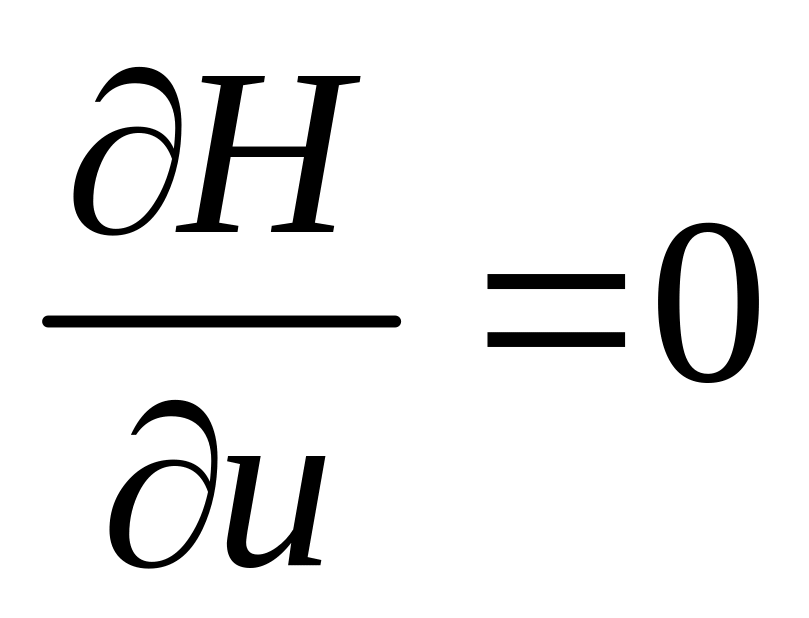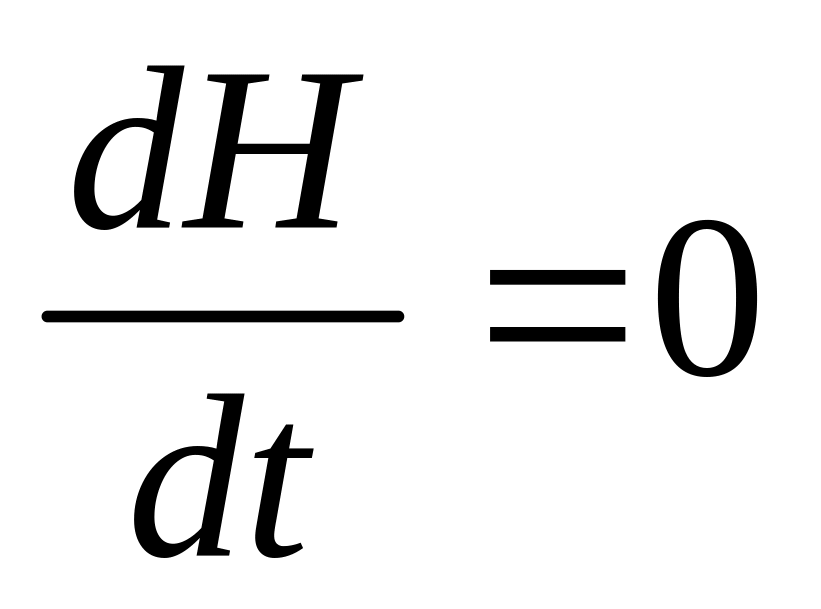1. Опт. Упр. u₀ нах-ся вн-ри доп обл-ти, тогда необх усл-ем max f-ии H яв-ся рв-во 0 ее произв-ых по ∂u: . Отсюда следует, что , значит,

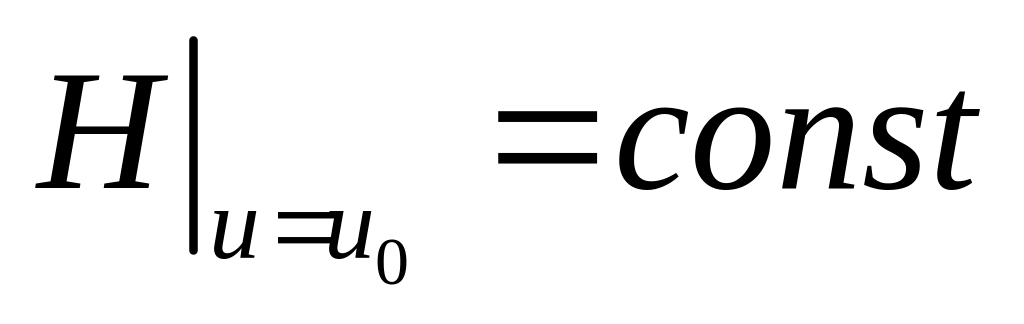
2. Опт Упр. u₀ проходит по гр-це доп. обл-ти. В этом случае: u₀=const, =>du/dt=0, H|_u0=const.

Т.о. вне завис-ти от того, проходит ли опт. траектория вн-ри или по гр-це доп. обл-ти, f H в любом случае на опт. траектории const. М/о показать, что на опт траектории она положительна: H(x₀,λ₀,u₀)=const>=0. При этом, ес время оконч-я прцса Т задано, то f H>0. Ес время окноч-я не задано, его нужнно Опр.-ть, то при опт У.-ии оно нах-ся из усл-я: H(x₀,λ₀,u₀,T)=0

22.Математическая формулировка принципа оптимальности.

Функциональные уравнения метода динамического программирования. - Критерий оптимальности n-стадийного процесса. Если учесть в этом уравнении уравнение состояния каждой стадии то придем к тому что критерий оптимальности будет зависеть от

обозначим через - максимальное значение критерия .

Очевидно, что будет так же зависеть от .

Учитывая что критерий есть аддитивная функция можно ее записать следующим образом где это суммарный критерий оптимальности для всех стадий кроме первой, его значение соответственно будет зависеть от . Подставим значение выражения (4) в уравнение (3) получим

Или (5). Обозначим максимальное значение второго слагаемого и подставим его значения в уравнения (5) и получим

Учитывая что согласно уравнению состояния

функциональное уравнение метода динамического программирования для дискретны процессов- это есть рекуррентное соотношение и согласно этому уравнению прежде чем найти управление на первой стадии необходимо найти максимум критерия оптимальности на всех последующих стадиях и начинать надо с последней стадии под номером N, поскольку за этой стадией нет других стадий которые могут повлиять на выбор управления на этой стадии.

23. Свойства озу в линейной постановке.

Пусть процесс описывается линейной системой уравнений: , , , где А(nn),B(rr) – заданны матрицей.

Критерий _s[u] – линейный функционал: - Свойство линейности.

Управление uU, т.е. если u₁U, u₂U, то управление U, ₁0, ₂0, ₁+₂=1.

ТЕОРЕМА: Если u₁ и u₂ – 2 решения ОЗУ, то управление является также решением ОЗУ, при ₁0, ₂0, ₁+₂=1.

ДОК-ВО: Пусть u₁ и u₂ – 2 решения ОЗУ, тогда управление является допустимым. Докажем, что оно является решением ОЗУ, т.е. _s[u]1, s=1,2,..2m.

Поскольку u₁ и u₂ – решения ОЗУ, то ₁[u₁]1, ₂[u₂]1.

Тогда

Данная теорема по двум управлениям u₁ и u₂ позволяет строить всевозможные управления в виде: ,

Аналогично доказывается, что если задано управления u_k (k=1,2,..r), то по ним можно построить любое управление в виде:

, , и такое управление будет решением ОЗУ.