Вариант 1

Часть 2

C1 Решите уравнение .

Укажите корни, принадлежащие промежутку .

Ответ: , где . Промежутку принадлежат корни , и .

Решение: перенесём все слагаемые в левую часть уравнения и разложим левую часть на множители. Получим: , где . Промежутку принадлежат корни , и .

Баллы	Критерии оценивания задания С1
2	Верно решено уравнение и верно произведён отбор корней
1	Верно решено уравнение, но неверно отобраны корни, принадлежащие указанному промежутку. Или верно отобраны корни уравнения, принадлежащие данному промежутку, но общее решение уравнения не указано
0	Решение не соответствует ни одному из критериев, перечисленных выше

C2 В правильной четырёхугольной пирамиде НАВСТ с вершиной Н все рёбра равны. Найдите угол между плоскостями АКВ и СМТ , где К – середина ребра НТ , а М – середина ребра НВ .

Ответ:

Решение: плоскость АКВ проходит через среднюю линию КР треугольника ТНС , а плоскость СМТ проходит через среднюю линию МЕ треугольника АНВ . Обозначим за О середину АВ , а за Д – середину ТС . Плоскость НДО является плоскостью симметрии, она перпендикулярна плоскостям АВК и СМТ . Обозначим за О₁ середину МЕ , за Д₁ – середину МР , а за Н₁ – точку пересечения ОД₁ и О₁Д . Угол ОН₁О₁ = – искомый острый угол между плоскостями АВК и СМТ . Найдём его. Пусть длины всех рёбер пирамиды равны 4 . Тогда ОД = 4 , ОО₁ = О₁Н = НД₁ = Д₁Д = . Опустим из точки Д₁ перпендикуляр Д₁Д₂ к основанию ОД . Тогда ОД₂ = ОД = 3 , Д₁Д₂ = . Угол ОД₁Д₂ равен половине искомого угла , тангенс угла ОД₁Д₂ равен . 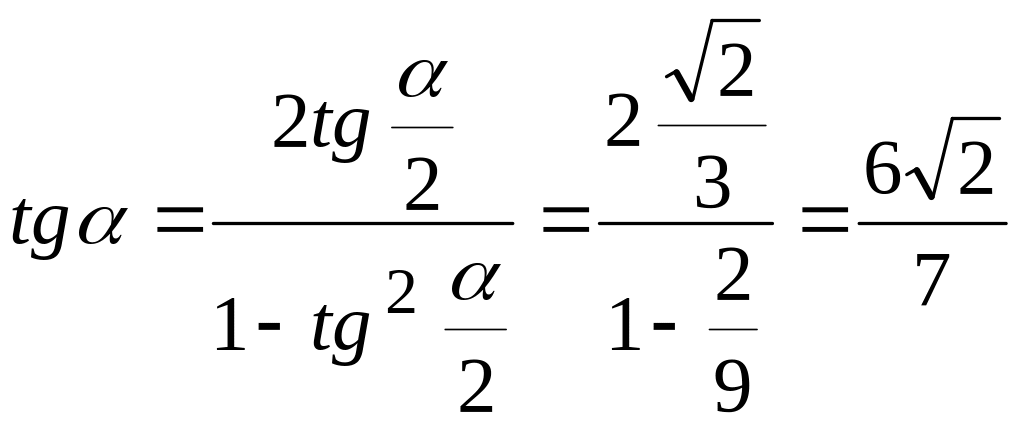Поэтому и .

Замечание: Возможна другая форма ответа, например

Баллы	Критерии оценивания задания С2
2	Обоснованно получен правильный ответ
1	Способ нахождения искомого угла правильный, но получен неверный ответ или решение не закончено
0	Решение не соответствует ни одному из критериев, перечисленных выше

C3 Решите систему неравенств

Ответ: х = -3.

Решение: рассмотрим первое неравенство системы:

.

С учётом полученного рассмотрим далее второе неравенство системы:

Таким образом, единственным решением системы является х = -3 .

Баллы	Критерии оценивания задания С3
3	Обоснованно получен правильный ответ
2	Все шаги решения выполнены. Дано верное и обоснованное решение одного из неравенств исходной системы, но при в целом правильном решении другого неравенства исходной системы допущена одна вычислительная ошибка
1	Дано верное и обоснованное решение одного из неравенств исходной системы
0	Решение не соответствует ни одному из критериев, перечисленных выше

C4 В треугольнике АВС точка К лежит на стороне АС , причём АК : КС = 2 : 3 . Точка М делит сторону АВ на два отрезка, один из которых втрое больше другого. Прямая, проходящая через точку М параллельно ВС , пересекает прямую ВК в точке Р . Найдите отношение ВР : КР .

Ответ: 5 : 7 или 5 : 1

Решение:

1-й случай. Пусть АМ : МВ = 3 : 1 . Обозначим МВ = b , АК = 2а . Тогда АМ = 3b , и КС = 3а . Пусть МТ параллельно ВС , точка Т лежит на АС . Тогда АТ : ТС = АМ : МВ = 3 : 1 , поэтому АТ = , ТС = и КТ = . Поэтому ВР : КР = ТС : КТ = 5 : 7 .

2-й случай. Пусть АМ : МВ = 1 : 3 . Обозначим АМ = b , АК = 2а . Тогда ВМ = 3b , и КС = 3а . Пусть МТ параллельно ВС , точка Т лежит на АС . Тогда АТ : ТС = АМ : МВ = 1 : 3 , поэтому АТ = , ТС = и КТ = . Поэтому ВР : КР = ТС : КТ = 5 : 1 .

Баллы	Критерии оценивания задания С4
3	В приведённом решении рассмотрены оба случая, и в каждом из них обоснованно получен верный ответ
2	В приведённом решении только в одном случае дано обоснование и получен верный ответ
1	В приведённом решении рассмотрен только один случай, при этом не дано обоснование или допущена вычислительная ошибка
0	Решение не соответствует ни одному из критериев, перечисленных выше

C5 Найдите все значения параметра а , при каждом из которых система уравнений имеет единственное решение.

Ответ: , .

Решение: раскроем модуль и преобразуем исходную систему уравнений. Получим:

.

Условия задают на координатной плоскости «уголок» с вершиной в точке (3 , 2) и лучами и , идущими вверх от точки (3 , 2) . Уравнение задаёт прямую, проходящую через точку (7 , 4) с угловым коэффициентом 1/а при и прямую x = 7 при а = 0. Поэтому исходная система уравнений имеет единственное решение тогда, когда прямая проходит через вершину (3 , 2) «уголка», или когда прямая пересекает ровно один из лучей «уголка». Первому случаю соответствует , а второму – условие .

Баллы	Критерии оценивания задания С5
4	Обоснованно получен правильный ответ
3	Решение в целом верное и обоснованное, но допущена одна вычислительная ошибка или описка
2	Ход решения в целом верный, но в решении содержатся существенные ошибки (например, не рассмотрен случай )
1	Имеется некоторое существенное продвижение в решении задачи (например, дана геометрическая интерпретация обоих уравнений системы)
0	Решение не соответствует ни одному из критериев, перечисленных выше

C6 Дайте обоснованные ответы на следующие вопросы:

а) найдутся ли три различных целых числа, которые, будучи расположены в одном порядке, образуют арифметическую прогрессию, а будучи расположены в некотором другом порядке, образуют геометрическую прогрессию?

б) найдутся ли пять различных целых чисел, четыре из которых, будучи расположены в одном порядке, образуют арифметическую прогрессию, а другие четыре из этих пяти, будучи расположены в некотором порядке, образуют геометрическую прогрессию?

в) найдутся ли четыре различных целых числа, которые, будучи расположены в одном порядке, образуют арифметическую прогрессию, а будучи расположены в некотором другом порядке, образуют геометрическую прогрессию?

Ответ: а) да ; б) да ; в) нет

Решение:

а) да, например, числа 1 , -2 , 4 образуют геометрическую прогрессию, а эти же числа, но в другом порядке -2 , 1 , 4 образуют арифметическую прогрессию.

б) да, например, числа -8 , -2 , 1 , 4 , 10. Причём числа -8 , -2 , 4 , 10 образуют арифметическую прогрессию, а числа 1 , -2 , 4 , -8 образуют геометрическую прогрессию.

в) нет. Действительно, пусть четыре целых числа, расположенные в определённом порядке, образуют геометрическую прогрессию. Тогда знаменатель этой прогрессии является рациональным числом, а сама последовательность имеет вид: , , , , где , , причём числа m и n не имеют общих делителей, а число k делится нацело на , . Но целые числа , , , ни в каком порядке не могут образовывать арифметическую прогрессию. Это следует из того, что сумма любых двух из них не равна сумме двух других, так как , и (в каждом из случаев три числа делятся на m , а одно не делится).

Баллы	Критерии оценивания задания С6
4	Даны вполне обоснованные ответы на все три вопроса
3	Даны обоснованные ответы на все три вопроса, но при ответе на вопрос в) допущена неточность в обосновании
2	Даны обоснованные ответы на два вопроса
1	Дан обоснованный ответ на один из вопросов
0	Решение не соответствует ни одному из критериев, перечисленных выше