
4.Приближенные вычисления
Пусть, требуется вычислить приближенное значение функции
f (х) = х7 - 2х6 + 3х2 - х + 3 в т. х = 2,02. Значение f в близкой к 2,02 точке х0 = 2 находится легко: f(2) = 13. График f в окрестности точки 2 близок к прямой у = f (х0) + f '(х0) (х - х0) — касательной к нему в точке с абсциссой 2. Поэтому f (2,02) ≈ у (2,02). Имеем f '(х) = 7х6 - 12х5 + 6х - 1, f '(х0) = f '(2) = 75 и f (х) ≈ у (х) = 13 + 75• 0,02 = 14,5.
Вычисления на калькуляторе дают результат f (2,02)≈ 14,57995.
Вообще для дифференцируемой в т. х0 функции f при ∆х, мало отличающихся от нуля, ее график близок к касательной (проведенной в точке графика с абсциссой х0 ), т. е. при малых ∆х
f(x)≈ f(x0)+ f '(x0)∆x (1)
Если
т. х0
такова, что значения
f
(х0)
и
f
'(х0)
нетрудно вычислить, то формула (1)
позволяет находить приближенные
значения
f
(х) при
х,
достаточно близких к
х0.
Так, при вычислении значения
 естественно взять в качестве
х0
число 4, т.к.4,08 близко к 4 и значения
f
(x0)
=
естественно взять в качестве
х0
число 4, т.к.4,08 близко к 4 и значения
f
(x0)
= и
f
'
(х0)
=
и
f
'
(х0)
=
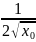 при
х0
= 4 найти нетрудно: f(4)
=
при
х0
= 4 найти нетрудно: f(4)
=
 =
2, f
'
(4) =
=
2, f
'
(4) = =
=
 . По (1) при ∆х= 0,08 получаем:
. По (1) при ∆х= 0,08 получаем:
≈2+ ∙0,08 =2,02.
Пр1.
Выведем из
ф.
(1) приближенную формулу
 ≈
≈ (2)
(2)
Возьмем
f
(х) =
 ,
х0
= 1 и x
= х0
+ ∆х = 1 +
∆х.
Имеем
,
х0
= 1 и x
= х0
+ ∆х = 1 +
∆х.
Имеем
f(x0)
=
 =1
и f'(x)
=
=1
и f'(x)
= ,
откудa
f'(x0)
= f'(
1) =
,
откудa
f'(x0)
= f'(
1) =
 . По ф(1)
. По ф(1)
f(x) =

В
частности,
 =
= ≈
≈ .
.
Значение также можно найти по формуле (2):
= ≈2(1+
≈2(1+ )=
2,02.
)=
2,02.
Пр 2. Выведем из ф (1) приближенную формулу
(1 + ∆х)n ≈ 1 + n∆х. (3)
Полагаем f(x) = xn, х0 = 1 и x = х0 +∆х = 1 + ∆х. Находим f(х0) = 1, f '(х) = пхn-1, откуда f '(х0) =n . По ф. (1) f (х) = (1 + ∆х)n ≈1 + п∆х.
Н-р,
1,001100
= (1 + 0,001)100
 1 + 100 • 0,001 = 1,1. Значение 1,001100,
вычисленное
на калькуляторе, равно 1,10512.
1 + 100 • 0,001 = 1,1. Значение 1,001100,
вычисленное
на калькуляторе, равно 1,10512.
5.Доказательство неравенств
Док-ть
cos
x>1-
 при x>0
при x>0
Док-во:
рассмотрим фун-ю у(х)= cos
x-1+
, замечаем, что у(0)= cos
0-1+
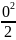 =0 (Находим
значение в крайних точках, здесь в 0,
т.к. x>0).
у'(х)=
-sin
x
-0+
=0 (Находим
значение в крайних точках, здесь в 0,
т.к. x>0).
у'(х)=
-sin
x
-0+
 -sin
x+x=x-sin
x
>0
при x>0.
(См. рис1.) T.е.
у'(х)
>0 при x>0
=> у(х) ↗
при x>0.
Получаем
(См. рис2.): у(0)=0, у(х) ↗при
x>0
=> у(х) >0 при x>0
=> cos
x-1+
>0 при x>0.
cos
x>1-
при x>0
-sin
x+x=x-sin
x
>0
при x>0.
(См. рис1.) T.е.
у'(х)
>0 при x>0
=> у(х) ↗
при x>0.
Получаем
(См. рис2.): у(0)=0, у(х) ↗при
x>0
=> у(х) >0 при x>0
=> cos
x-1+
>0 при x>0.
cos
x>1-
при x>0
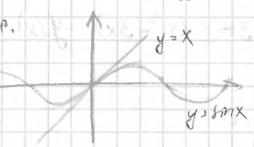 рис1
рис1 рис2
рис2
Итоги: 1.ввести функцию
2.если дан промежуток взять крайнее его значение и подставить
3.найти производную, определить знак, делаем вывод ↗или↘
4.возвращаемся к начальному примеру
6.Нахождение числа корней уравнения
Найдем число корней уравнения 2х3 - 3х2 - 12х – 11=0
Рассмотрим функцию f(x) = 2х3 - 3х2 - 12х -11. D (f) = (-∞;∞). Для отыскания критических точек функции f найдем f'(x): f'(x) = 6х2 - 6х - 12. f'(x)=0 в точках х = -1 и х = 2. Заполним таблицу:
x |
(-∞, -1) |
-1 |
(-1; 2) |
2 |
(2; ∞) |
f' (x) |
+ |
0 |
- |
0 |
+ |
f (х) |
↗ |
-4 |
↘ |
-31 |
↗ |
|
|
max |
|
min |
|
На (-∞;-1] ф-я возрастает от -∞ до -4, поэтому на этом пром-ке ур-е f (х) = 0 корней не имеет. На [-1; 2] ур-е не имеет корней, т.к. на этом пром-е f убывает от -4 до -31. На [2; ∞) функция f возрастает от -31 до ∞, на этом пром-е ур-е f (х) = 0 имеет один корень (по теореме о корне: Пусть фун-я возрастает(убыв.) на пром-ке I, число а-любое из значений, принимаемых f на этом пром-ке.Тогда ур-е f(x)=a имеет единств-й корень в пром-ке I). Итак, ур-е 2х3 - 3х2 - 12х – 11=0 имеет один корень, и этот корень принадлежит интервалу (2; +∞).
