Вопрос № 24

Докажите формулу распределения ускорений точек плоской фигуры

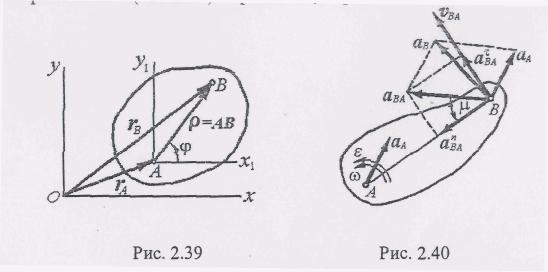
Пусть плоская фигура (S) движется относительно непод­вижной системы координат Оху. В этой системе положения по­люса А и произвольной точки В определяются соответственно радиус-векторами rА и rB (рис. 2.39).

Скорость произвольной точки В можно определить с по­мощью формулы распределения скоростей

(1)

где р =АВ радиус-вектор, проведенный из полюса А в точку В. Дифференцируя равенство (1) по времени, получим

(2)

Здесь , т.е. соответственно равны ускорениям полюса А и точки В. Производная есть вектор углового ускорения фигуры,направленный (как и (О) перпендикулярно к плоскости фигуры.

Кроме того, согласно формуле дифференцирования век­тора, постоянного по модулю (см. формулу (а), п. 2.16),

. Тогда последнее слагаемое формулы (2), раскрыв двойное векторное произведение, можно представить так

(3)

(4)

В результате равенство (2)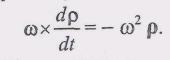 окончательно можно записать так:

(5) Введем обозначения:

(6)

Векторы A^tba и Aⁿba представляют те касательное и нормальное ускорения, которые имела бы точка В, если бы фигура (S) совер­шала только вращение вокруг полюса А. Вопрос о направлении этих векторов изучен нами ранее, однако, пользуясь правилом составления векторного произведения, легко убедиться, что Aⁿba имеет направление, совпадающее с вектором SA (от точки к полюсу), а A^tba - перпендикулярно ВА.

Модули этих векторов определяются так:

(7)

Используя обозначения (6), окончательно находим фор­мулу распределения ускорений

(8) или

(9)

где

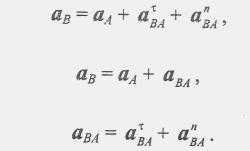(10)Таким образом, ускорение любой точки В плоской фигу­ры в каждый данный момент равно геометрической сумме двух ускорений: ускорения произвольного полюса А и ускорения точки В в ее вращательном движении вместе с плоской фигурой вокруг этого полюса.Так как модуль ускорения точки В при вращении фигуры вокруг полюса А находится так: (И)

Угол M., который образует вектор Aba с направлением ВА, определяется из следующего равенства:

(12)

Этот угол M одинаков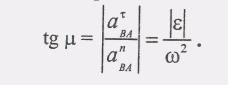 для всех точек плоской фигуры. Получен­ные результаты позволяют построить вектор Ab так, как это пока­зано на рис. 2.40.

Вопрос №25. Дайте определение мгновенного центра ускорений. Как определяется его положение? Как оп-ределяются ускорения точек плоской фигуры с помощью мгновенного центра ускорений.

При непоступательном движении плоской фигуры в ее плоскости на фигуре (или на связанной с ней подвижной плоско­сти) в каждый момент времени имеется точка Q, ускорение которой равно нулю. Эта точка называется мгновенным цен­тром ускорений.

П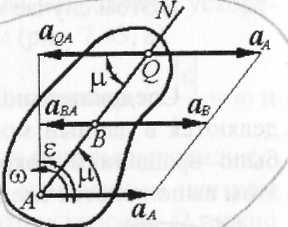 оложение мгновенного центра ускорений в общем слу­чае может быть определено, если известно ускорение какой-либо точки А плоской фигуры, а также ее угловая скорость и угловое ускорение. Тогда положение мгновенного центра ускорений

определяется следующим образом (рис. 2.41) 1) находим значение угла M из формулы

2 ) из точки А, ускорение которой известно, под углом M к вектору аА проводим полупрямую AN, которая должна быть отклонена от аА на угол M в сторону вращения фигуры, если вращение ускоренное, и против вращения, если оно является замедленным, т.е. в сторону направления углового ускорения E, показанного на рис. 2.41 дуговой стрелкой;

3) на полученной полупрямой AN отложим отрезок

Конец Q этого отрезка и будет мгновенным центром ускорения. В самом деле, примем точку А за полюс, тогда по форму­ле распределения ускорений

Подставляя сюда значение AQ из равенства (2), находим, что aQA = аА, т.е. модуль вращательного ускорения aQA точки Q вокруг полюса А равен модулю ускорения аА этого полюса. С другой стороны, как было показано в предыдущем параграфе, угол между ускорением точки относительно полюса и направле­нием на полюс не зависит от выбора полюса. Следовательно, aQA составляет с направлением QA угол µ. Такой же угол составляет и вектор аА с отрезком AQ. Поэтому векторы аА и aQA параллель­ны, но противоположно направлены. Кроме того, aQA = - аА, а тогда аQ = 0. Таким образом, мы доказали, что точка Q - мгно­венный центр ускорений.

Если точку Q выбрать за полюс, то, поскольку aQ = 0, ускорение любой точки М плоской фигуры, согласно формуле (3), будет равно ускорению точки М во вращательном движении этой точки вокруг мгновенного центра ускорений, т.е.

aM = aMQ.

В этом случае модуль ускорения точки М будет

(5)

С ледовательно, ускорения точек плоской фигуры опре­деляются в данный момент времени так, как если бы движение было вращением вокруг мгновенного центра ускорений. При этом выполняются следующие соотношения:

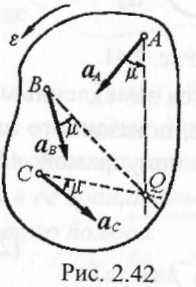
т.е. ускорения точек плоской фигуры пропор­циональны расстояниям от них до мгновенного центра ускорений. Поле ускорений точек пло­ской фигуры показано на рис. 2.42. Следует иметь в виду, что при движении плоской фигу­ры положение ее мгновенного центра ускоре­ний непрерывно меняется, и положение мгно­венного центра скоростей Р и мгновенного центра ускорений Q в данный момент времени не совпадают. Например, при качении без скольжения колеса по прямолинейному рельсу, когда ско­рость центра колеса постоянна, мгновенный центр ускорений в каждый момент времени совпадает с центром колеса, тогда как мгновенный центр скоростей Р находится в точке касания колеса с рельсом. Мгновенные центры скоростей и ускорений совпадают лишь тогда, когда тело вращается вокруг неподвижной оси.