Вопрос № 13Вывести формулы равномерного и равнопеременного вращательного движения твердого тела. Начертите график равнопеременного вращательного движения

Вращение тела называют равномерным, если угловая скорость тела постоянна, т.е. В этом случае

(1) .Произвольную постоянную С определяем из начального условия В результате находим Тогда (2)

Равенство (2) называется законом равномерного враща­тельного движения твердого тела. При это равенство уп­рощается.

Равнопеременным вращением называется такое враща­тельное движение тела, при котором его угловое ускорение по­стоянно, т.е. Вэтом случае (3)Из начального условия находим ~ Тогда (4)Равенство (4) называется законом изменения угловой скорости при равнопеременном вращательном движении тела. Далее • (5)

Из начального условия находим Тогда окончательно (6)

Равенство (6) называется законом равнопеременного вращательного движения твердого тела. Легко заметить анало­гию между полученными формулами (2) и (6) и формулами рав­номерного и равнопеременного движения точки. Соответствующие формулы совпадают с точностью до обозначений.

Вопрос № 14 , 15

Вывести формулу для определения скорости точек тела, вращающегося вокруг неподвижной оси. Вывести формулы для определения ускорения точек тела, вращающегося вокруг неподвижной оси.

Пусть вращение тела вокруг неподвижной оси задано уравнением (1) Найдем распределение скоростей точек тела при его вращении. Воспользуемся при этом естественным способом за­дания движения точки. Рассмотрим движение какой-нибудь точ­ки М тела. При вращении тела точка М будет описывать окруж­ность, радиус которой обозначим R (рис. 2.21).

С оставим уравнение движения точки М по ее траекто­рии. За начало отсчета примем начальное положение Мо, а за по­ложительное направление дуги s - направ­ление отсчета угла поворота ф. Тогда урав­нением движения точки М по ее траектории будет (2) а следовательно, проекция скорости точки М на направление касательной определится следующим образом:

(3) или

(4) Эту скорость точки М, в отличие от угловой скорости тела, часто называют линейной скоростью. Та­ким образом, линейная скорость какой-либо точки вращающего­ся твердого тела равна произведению угловой скорости тела на расстояние от этой точки до оси вращения. Вектор V скорости точки М направлен по касательной к окружности, которую описывает точка М, т.е. перпендикулярен к радиусу этой окружности. Модуль V вектора скорости V равен

(5)

Так как угловая скорость со является кинематической ха­рактеристикой всего тела в целом, то из формулы (5) следует, что скорости точек тела пропорциональны расстояниям этих точек до оси вращения.

Ускорение точки М находим, определив сначала каса­тельное и нормальное ускорения:

Тогда модуль полного ускорения точки М (7)

Угол, образованный вектором ускорения точки М с ра­диусом описываемой точкой окружности, определяется так:

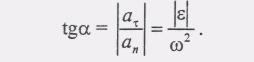(8)

Из формулы (8) следует, что ускорения точек вращающе­гося тела образуют в данный момент один и тот же угол а с ра­диусами описываемых ими окружностей. В частном случае рав­номерного вращения Е=0, поэтому А=0 и, следовательно, полное ускорение по модулю равно нормальному и направлено к оси вращения.

вопрос № 16 , 17

Вывести векторную формулу для скорости точек тела, вращающегося вокруг неподвижной оси. Вывести векторные формулы для ускорений точек тела, вращающегося вокруг неподвижной оси и провести их анализ

Рассмотрим твердое тело, вращающееся вокруг непод­вижной оси Oz с угловой скоростью Определим скорость произвольной точки М этого тела. Введем прямоугольную систему координат с началом на оси вращения и неизменно связанную с те­лом (рис. 2.22).В этом случае

(1)

Здесь следует заметить, что в разло­жении (1) х, у, z и вектор k постоянны, т.е. не зависят от времени, a i и j зависят от времени, так как вращаются вместе с телом.

Т огда для скорости точки М имеем(2)

Производные от единичных векторов, входящие в формулу (2), есть скорости концов этих векторов. Например, при ф > О вектор скорости конца i направлен парал­лельно j в положительном направлении оси Оу, а вектор скорости

конца j направлен параллельно i в отрицательном направлении оси Ох. Модуль каждой из этих скоростей равен \ф\.

Тогда

Далее, учитывая, что j =k*x, a -i =k * j, получим

(3)

Подставляя формулы (3) в равенство (2) и используя то,

что , найдем

(4)

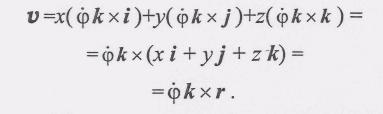
Назовем вектор фк вектором угловой скорости со, тогда

(5)

Как видно из равенства (5), вектор угловой скорости те­ла направлен вдоль оси вращения так, чтобы наблюдатель, смотрящий с его конца, видел вращение тела против хода часо­вой стрелки.

Вектор ф можно расположить в любом месте оси враще­ния, т.е. ф — скользящий аксиальный вектор.

Перепишем теперь формулу (4) с учетом (5), тогда

(6)

Вектор скорости любой точки тела, вращающегося во­круг неподвижной оси, равен векторному произведению вектора угловой скорости тела на радиус-вектор этой точки, проведен­ный из произвольного центра, взятого на оси вращения. Формула (6) называется формулой Эйлера.

Вопрос № 18

Дайте определение плоскопараллельного движения твердого тела, обоснуйте и запишите уравнения плоскопараллельного движения. Каковы основные кинематические характеристики плоскопараллельного движения.

Движение абсолютно твердого тела называется плос­копараллельным (или плоским), если все точки этого тела дви­жутся в плоскостях, параллельных некоторой неподвижной плоскости. Примером плоскопараллельного движения твердого тела может служить движение колеса по прямолинейному рельсу или движение шатуна кривошипно-ползунного механизма.

Р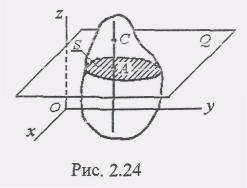 ассмотрим плоскопараллельное движение произвольно­го твердого тела. Пусть все точки тела перемещаются в плоскостях, параллельных неподвижной плоскости xОy. Пересечем рас­сматриваемое тело плоскостью Q, параллельной неподвижной плоскости хОу (рис. 2.24). В результа­те в сечении получим некоторую фи­гуру S. Из определения плоскопарал­лельного движения твердого тела сле­дует, что плоская фигура S перемеща­ется с данным телом и остается во все время этого движения в плоскости Q. Следовательно, любой отрезок АС, взятый в теле и перпендикулярный к плоскости хОу, будет дви­гаться параллельно своему первоначальному положению, т.е. поступательно. Скорость и ускорение любой из точек отрезка АС будут параллельны плоскости хОу. Но тогда для определения движения всех точек тела, лежащих на отрезке АС, достаточно знать движение одной точки этого отрезка, а за такую точку можно взять точку А плоской фигуры S. Отсюда следует, что для определения плоскопараллельного движения твердого тела необ­ходимо знать движение лишь одной точки на каждой прямой, проведенной перпендикулярно неподвижной плоскости хОу, т.е. достаточно знать движение плоской фигуры S в ее плоскости.

Итак, задание плоскопараллельного движения твердого тела и изучение этого движения сводится к заданию движения одного сечения тела. Поэтому в дальнейшем плоскость Q будем совмещать с плоскостью чертежа, а вместо всего тела изображать только плоскую фигуру - сечение тела 5, и изучать движение точек этого сечения в его плоскости. Строго говоря, рассматривая движение плоской фигуры 5 в ее плоскости, мы рассматриваем движение всей плоскости, неизменно связанной с движущейся фигурой относительно неподвижной плоскости, так что вопрос сводится к рассмотрению движения подвижной плоскости отно­сительно неподвижной. Положение сечения S в его плоскости определяется положением двух точек этого сечения или положе­нием отрезка прямой, соединяющей эти две точки, например, отрезка АВ. Т.е. кинематика плоскопараллельного движения тела сводится к кинематике движения отрезка прямой в плоскости.

Пусть- две точки плоской фигуры, находящейся в плоскости xOy (рис 2.25, а). Расстояние d ме­жду этими точками определяется следующим равенством:

(1)

Так как это расстояние неизменно, то из четырех коор­динат х1А, у1А и х1В, у1В независимых только три, т.е. положение отрезка на плоскости вполне определяется тремя независимыми параметрами. В качестве таких независимых параметров можно взять координаты одной из точек, например, координаты х1А и у1А точки А и угол ф, который отрезок АВ образует с осью X1.

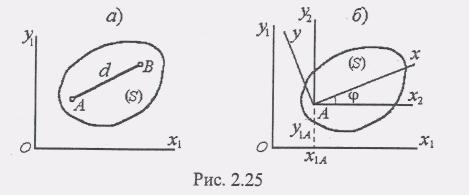
Точку А, выбранную для определения положения сече­ния S, будем в дальнейшем называть полюсом. Проведем через этот полюс координатные оси Ах и Ау, неизменно связанные с плоской фигурой и движущиеся вместе с ней относительно не­подвижных осей координат Ох1у1 . Для того, чтобы знать поло­жение плоской фигуры, или, что то же самое, положение под­вижных осей координат Оху относительно неподвижных осей ОХ1у1 достаточно задать координаты Х1А, у1А полюса А и угол ф, который составляет подвижная ось Ах с неподвижной Ох1. При этом условимся считать угол поворота ср положительным, когда он отложен от оси ОХ1 в направлении, обратном движению часо­вой стрелки (рис. 2.25, б). При движении тела величины x1A,y1A и ф будут изменяться с течением времени. Чтобы знать закон дви­жения тела, т.е. знать его положение в пространстве в любой мо­мент времени, надо знать зависимости:

(2)Уравнения (2), полностью определяющие положение плоской фигуры в любой момент времени, называются уравне­ниями плоскопараллельного движения твердого тела.

В заключение отметим, что частными случаями движе­ния плоской фигуры в ее плоскости являются поступательное и вращательное. Определения, свойства этих движений и соответ­ствующие формулы изучены нами ранее.

Вопрос № 19

Сформулируйте и докажите теоремы о перемещениях плоской фигуры

Теорема 1. Всякое перемещение плоской фигуры в ее плоскости можно осуществлять посредством поступательного перемещения вместе с произвольной точкой (полюсом) и враща­тельного перемещения вокруг этого полюса.

Пусть плоская фигура (S) за некоторый промежуток вре­мени переместилась из положения I в положение II так, что отре­зок АВ занял положение А1В1 (рис. 2.26). Если за полюс принять точку А, то это перемещение можно совершить следующим образом. Сначала сообщим пло­ской фигуре поступательное пе­ремещение, которое переводит полюс А в положение А1, при этом отрезок АВ займет положе­ние А1В’1 и все точки плоской фигуры получат перемещения, геометрически равные АА1, а затем сообщим плоской фигуре вращение вокруг точки А1 которое повернет отрезок А1В1 на угол В’1А1В1 в положение А1В1.

Л егко убедиться в том, что, выбирая различные точки плоской фигуры за полюсы при перемещении ее из одного поло­жения в другое, мы изменяем только поступательное перемеще­ние, угол же поворота и направление вращательного перемеще­ния плоской фигуры от выбора полюса не зависят.

В самом деле, тот же переход фигуры (S) из положения I в положение II можно осуществить, приняв за полюс точку В и сообщив плоской фигуре поступательное перемещение, которое переводит полюс В в положение В1, при этом отрезок АВ займет положение А1В1, и все точки плоской фигуры получат перемеще­ния, геометрически равные ВВ1 и отличные от АА1, а затем, по­вернув плоскую фигуру вокруг точки В1 на угол А’1В1А1, в поло­жение В1А1. По свойству поступательного перемещения отрезки А1В’ и А’1В1 параллельны отрезку АВ. Следовательно, А1В1'||А’1В1 и ZB’1A1B1=ZA’1B1A1=ф. Кроме этого, поворот вокруг точек А1 и В1 в том и другом случаях происходит в одну и ту же сторону.

Вопрос № 20

Докажите формулу распределения скоростей точек плоской фигуры

Выше было показано, что плоскопараллельное движение твердого тела слагается из поступательного движения, при кото­ром все точки тела движутся со скоростью полюса Va, и из вра­щательного движения вокруг полюса. Покажем теперь, что ско­рость любой другой точки В тела геометрически складывается из скоростей, которые она получает в каждом из этих движений.

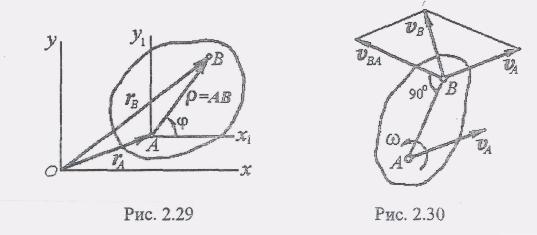
Пусть плоская фигура движется относительно непод­вижной системы координат Оху. В этой системе положения по­люса А и произвольной точки B определяются соответственно радиус-векторами ra и rb. Между этими векторами ra и rb и век­тором р = АВ (рис. 2.29) в любой момент времени имеет место следующее соотношение:

(1)Вектор р = AB определяет положение произвольной теч­ки В относительно системы Ах1у1 перемещающейся вместе с полюсом А поступательно. Подчеркнем еще раз, что движение се­чения по отношению к осям Ах1У1 представляет собой вращение вокруг полюса А. Дифференцируя обе части равенства (1) по времени, по­лучим (2) В полученном равенстве (2) . Что же

касается , то это - скорость, которую точка В получает при вращении вокруг полюса A. Обозначим эту скорость через

(3)Вектор р = АВ есть постоянный по модулю вектор, из­меняющийся при движении фигуры только по направлению. Для него справедлива формула (а) п. 2.16, т.е. (4)Тогда формула распределения скоростей примет вид

5)

(6)

Следовательно, скорость Vb любой точки плоской фигу­ры в каждый данный момент равна геометрической сумме двух скоростей: скорости VA другой, произвольно выбранной и принятой за плюс, точки А и скорости Vba точки В в ее вращении вме­сте с плоской фигурой вокруг этого полюса. Вектор Vba направ­лен перпендикулярно АВ в сторону вращения фигуры, а по моду­лю эта скорость определяется так:

(7)

Таким образом, определив вращательную скорость Vba точки В вокруг полюса А и зная скорость VA этого полюса, мы можем найти искомую скорость Vb точки В как диагональ парал­лелограмма, построенного на скоростях VA и VBa (рис. 2.30).

Вопрос № 21

Сформулируйте и докажите теорему о проекциях скоростей двух точек плоской фигуры на прямую, соединяющую эти точки

Определение скоростей точек тела с помощью доказан­ной формулы распределения скоростей часто связано с достаточ­но сложными расчетами. Однако, используя упомянутую форму­лу, можно получить другие более удобные и простые методы оп­ределения скоростей точек пло­ской фигуры (рис. 2.31).

О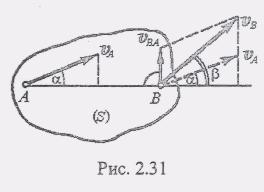 дин из таких методов дает теорема: проекции скоростей двух точек плоской фигуры на прямую, соединяющие эти точки, равны между собой.

Рассмотрим какие-нибудь две точки А я В, движущиеся в своей плоскости плоской фигуры (S). Предположим, что извест­ны модуль и направление скорости точки А и направление скоро­сти точки В. Принимая точку А за полюс, можно записать, что

(1)

Проецируя обе части этогоравенства на линию АВ и учитывая, что вектор Vba перпендикулярен к АВ, приходим к результату

(2)

Доказанная теорема* позволяет находить модуль скоро­сти Vb точки В, если известны модуль и направление скорости Va точки А и направление скорости Vb точки В.

Вопрос № 22

Опишите, как определяются скорости точек плоской фигуры и её угловая скорость с помощью мгновенного центра скоростей

Другой простой и наглядный способ определения скоро­стей точек тела при плоскопараллельном движении основан па понятии о мгновенном центре скоростей. Формула распределения скоростей, полученная ранее, основывалась на представлении о перемещении плоской фигуры

в виде геометрической суммы поступательного перемещения по­люса и вращательного перемещения вокруг полюса (теорема 1). Упрощение картины распределения скоростей можно получить, основываясь на представлении перемещения плоской фигуры по теореме Эйлера - Шаля (теорема 2). Докажем теорему.

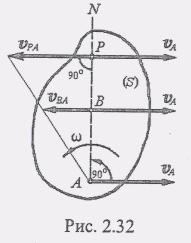
При всяком непоступательном перемещении плоской фигуры существует единственная точка этой фигуры, скорость которой в данный момент равна нулю. Точка Р плоской фигуры, скорость которой в данный момент вре­мени равна нулю, называется мгновенным центром скоростей. Для доказательства восстановим из точки А плоской фигуры перпендикуляр AN к направлению скоро­сти Va так, чтобы угол 90 между Va и ли­нией AN был отсчитан в сторону вращения плоской фигуры (рис. 2.32). Тогда, по до­казанной ранее формуле, вектор скорости любой точки В, лежащей на перпендику­ляре AN,

(1)

а величина скорости Vb в силу того, что Va и Vb лежат на одной прямой, будет

(2)

Изменяя расстояние точки В от точки А, можно найти при ф не = 0 такую точку Р, чтобы VPA = -VA, тогда

(3) при этом

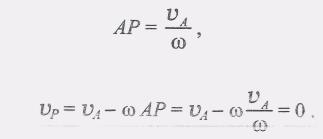(4)

Таким образом, теорема доказана.

Вопрос № 23

Опишите частные случаи определения положения мгновенного центра скоростей

1, Пусть скорости Va и Vb любых двух течек А к В парал­лельны друг другу и при этом линия АВ не перпендикулярна к VA, а следовательно, и к VA (рис. 2.34). Из теоремы о проекциях ско­ростей двух точек на прямую, соединяющую эти точки, следует, что но а = B, поэтому VB = VA и, следовательно, Vb = VA .

Т аким образом, в рассматриваемом случае скорости всех точек плоской фигуры в данный момент равны и по модулю, и по направлению. Такое состояние плоской фи­гуры называется мгновенно поступатель­ным. Так как перпендикуляры, восстанов­ленные из точек А и В к скоростям этих то­чек, не пересекаются, то в рассматриваемом случае в данный момент мгновенный центр скоростей находится в бесконечности. Уг­ловая скорость со плоской фигуры в этот момент равна нулю.

2. Пусть скорости VA и Vb точек А и В параллельны друг другу и эти точки лежат на одном перпендикуляре к данным ско­ростям. В этом случае при VA не = Vb мгновенный центр скоростей Р определяется построениями, показанными на рис. 2.35, а и б.

Справедливость построения следует из пропорции (6) предыдущего параграфа. Е этом случае для нахождения мгно­венного центра скоростей Р нужно, кроме направлений, знать еще и модули скоростей Va и Vb.

3. Е практических задачах часто приходится иметь дело со случаем, когда плоская фигура катится без скольжения по не­которой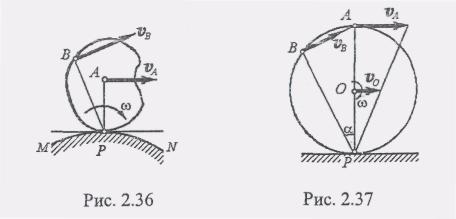 неподвижной кривой MN (рис. 2.36).

В этом случае скорость точки касания контура плоской фигуры с кривой MN равна нулю, так как точки касания обоих тел при отсутствии скольжения должны иметь одинаковые ско­рости, а кривая MN неподвижна. Отсюда следует, что точка каса­ния Р является мгновенным центром скоростей плоской фигуры. В качестве примера на рис. 2.37 показано распределение скоро­стей точек колеса, которое катится без скольжения по неподвиж­ному прямолинейному рельсу.