8. Проверим гипотезу о параметрах нормального распределения
Статистика для мат. ожидания |
|
Статистика для дисперсии |
||
|
||||
128,66449483 |
|
23,85966617 |
||
|
||||
|
|
|
|
|
Функция t(N-1)() |
|
Величины C1() и C2(a) |
||
|
||||
1,66039116 |
|
77,04633 |
123,22522 |
|
|
||||
Случайная величина
имеет нормальное распределение с
параметрами
и
.
Пусть
-
первая повторная выборка.
1.
Для проверки
используем статистику
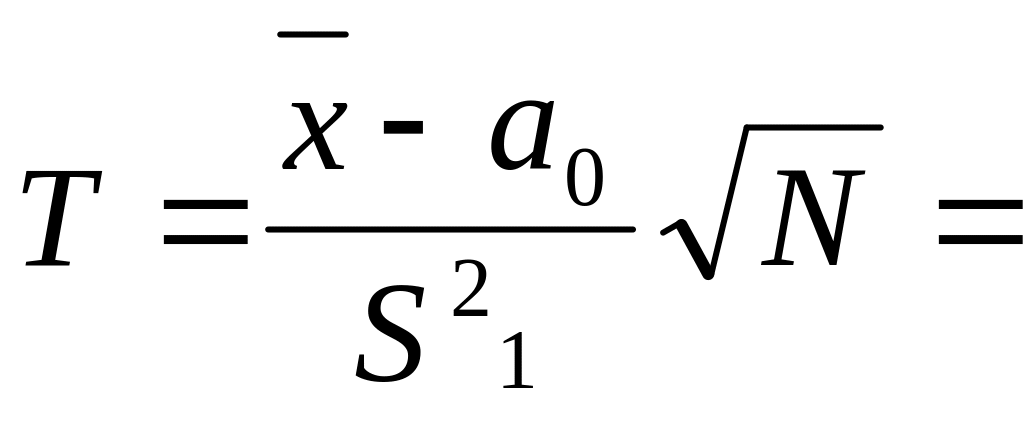128,66449483,
которая имеет распределение Стьюдента
с
степенями
свободы. Для
0.1 ,
=
1,66039116;
Так как |T|
>
,
гипотеза
противоречит экспериментальным данным
при заданном уровне значимости
,
т.е. отвергаем гипотезу
.
2.
Для проверки
используем статистику
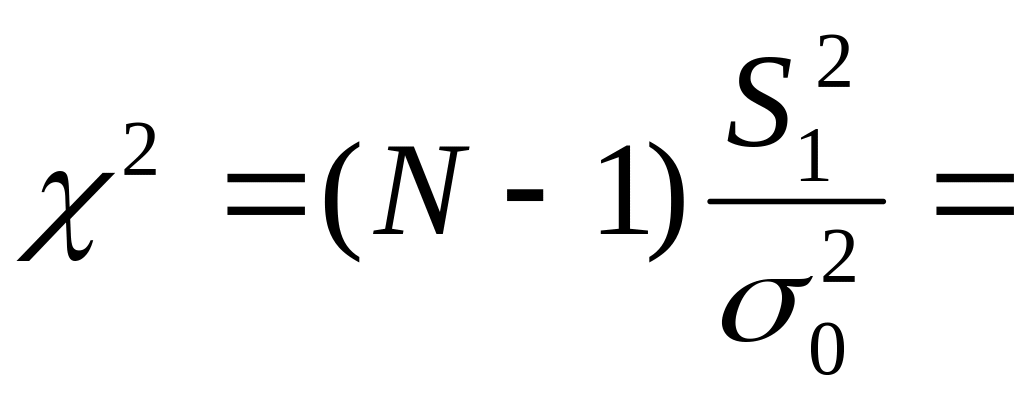23,85966617,
которая имеет
-
распределение с
степенью
свободы. Для
0,1,
77,04633;
123,22522;
Так как
не
выполняется, то гипотеза противоречит
экспериментальным данным при заданном
уровне значимости
.
10. Проверка гипотезы о равенстве средних.
Пусть мы имеем
две повторные выборки
и
,
из генеральных совокупностей с нормальным
распределением, параметры которых есть
и
соответственно.
Проверяем гипотезу
.
=
-1,50885;
,
Для этого используем
статистику
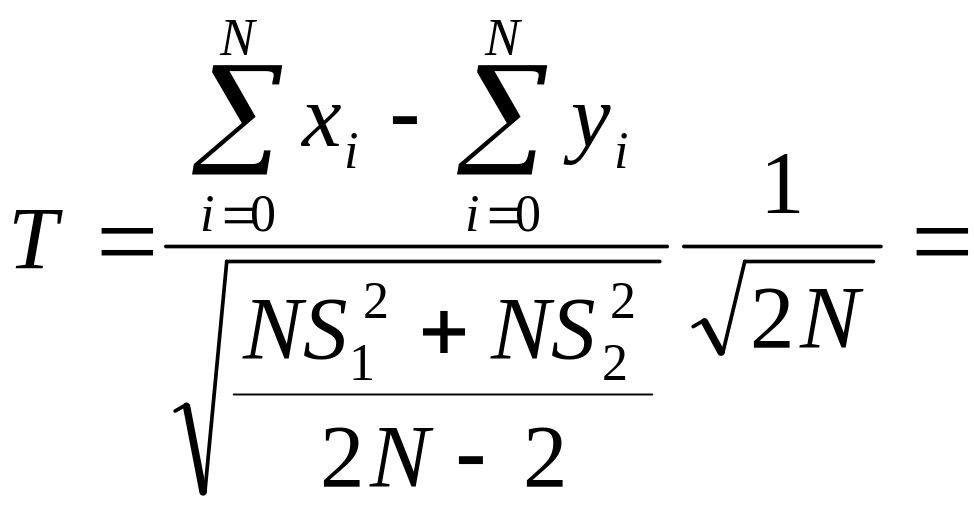0,55414720,
которая имеет распределение Стьюдента
с
степенью свободы. Для
0.1 ,
1,65258578
Так как
,
гипотеза
не противоречит экспериментальным
данным при заданном уровне значимости
.