Построим для первой выборки график эмпирической функции, гистограмму и сглаженную гистограмму.

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тверской Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ Рассчётно–графическая работа.doc

Скачиваний:

Добавлен:

29.07.2019

Размер:

536.58 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Министерство образования

Тверской Государственный Университет

Факультет Прикладной Математики и Кибернетики

Кафедра Информатики

Рассчётно–графическая работа

по Теории Вероятностей и Математической Статистики

Студент 36 группы

Бесараб Андрей Олегович

Руководитель:

Захарова Ирина Владимировна

Тверь, 2011

Начальные данные:

a	-1.5
²	0,25
	0,95
	0, 1
a₀	1
₀²	0,16

Сгенерируем две повторных выборки с нормальным распределением. Известно, что наблюдаемая случайная величина имеет нормальное распределение с параметрами a = -1,5, =0,25.

Упорядочиваем данные для упрощения работы.

Выборки (№1)
Выборки (№1)
	Повторная выборка X=(X1,…,X100)	Повторная выборка 2 Y=(Y1,…,Y100)
	Повторная выборка X=(X1,…,X100)	Повторная выборка 2 Y=(Y1,…,Y100)
	-1,105	-0,93993
	-1,11174	-1,00814
	-1,18777	-1,01476
	-1,1878	-1,02236
	-1,23798	-1,09299
	-1,2626	-1,11323
	-1,26843	-1,13402
	-1,27042	-1,14077
	-1,28311	-1,16093
	-1,2947	-1,16316
	-1,29617	-1,16661
	-1,29687	-1,21449
	-1,29923	-1,23389
	-1,30484	-1,23847
	-1,31737	-1,24784
	-1,32524	-1,25046
	-1,333	-1,26422
	-1,34287	-1,26787
	-1,34516	-1,27063
	-1,35504	-1,27283
	-1,35643	-1,27319
	-1,36924	-1,28696
	-1,36967	-1,29122
	-1,37335	-1,30873
	-1,38311	-1,31527
	-1,3874	-1,33002
	-1,38819	-1,33005
	-1,39999	-1,33074
	-1,41506	-1,35365
	-1,42491	-1,36596
	-1,42694	-1,39441
	-1,43109	-1,40200
	-1,43175	-1,40352
	-1,43802	-1,41294
	-1,45216	-1,41924
	-1,45336	-1,42081
	-1,46463	-1,42861
	-1,46845	-1,42958
	-1,47196	-1,44064
	-1,47201	-1,45071
	-1,47275	-1,45439
	-1,47843	-1,45585
	-1,48264	-1,46414
	-1,48486	-1,47143
	-1,49114	-1,47253
	-1,49237	-1,47874
	-1,49303	-1,47924
	-1,49493	-1,48181
	-1,49814	-1,48288
	-1,50266	-1,48884
	-1,50774	-1,49405
	-1,51023	-1,50759
	-1,51692	-1,51124
	-1,51824	-1,52420
	-1,52297	-1,52578
	-1,52931	-1,54495
	-1,52993	-1,55526
	-1,53833	-1,56168
	-1,54031	-1,57041
	-1,54675	-1,57295
	-1,56241	-1,57938
	-1,56878	-1,59888
	-1,57011	-1,60765
	-1,57019	-1,60881
	-1,57061	-1,61199
	-1,57107	-1,61309
	-1,57924	-1,61891
	-1,58529	-1,61933
	-1,59248	-1,62380
	-1,59514	-1,62812
	-1,60848	-1,63377
	-1,61758	-1,65362
	-1,62735	-1,65664
	-1,63674	-1,66086
	-1,64245	-1,66799
	-1,64354	-1,67536
	-1,6472	-1,69579
	-1,65076	-1,70101
	-1,69571	-1,70519
	-1,70495	-1,70934
	-1,71763	-1,72770
	-1,72474	-1,72884
	-1,72759	-1,72987
	-1,73151	-1,74564
	-1,73965	-1,76599
	-1,74173	-1,76699
	-1,74195	-1,79095
	-1,74614	-1,79411
	-1,75611	-1,82608
	-1,77006	-1,82841
	-1,79764	-1,83231
	-1,81385	-1,84625
	-1,8306	-1,88414
	-1,89272	-1,91007
	-1,89751	-1,92625
	-1,91426	-1,95746
	-1,91503	-2,00496
	-1,96376	-2,02530
	-1,98977	-2,10972
	-2,05107	-2,11051

Найдём для первой выборки:

Найти выборочное среднее и дисперсию, экстремальные значения, размах, выборочную медиану.

Выборочным средним является число .

_{Выборочной
дисперсией –

.}

Основные сведения (№2)
Основные сведения (№2)
	Выборочное среднее (X\|)
	Выборочное среднее (X\|)
	-1,5265814
	-1,5265814

	Выборочная дисперсия (S^2)
	Выборочная дисперсия (S^2)
	0,038175466
	0,038175466

	Экстремальные значения (X1, X100)


	-2,05107
	-1,105

	Размах выборки
	Размах выборки
	0,94607
	0,94607

	Медиана
	Медиана
	-1,5052
	-1,5052

Построим для первой выборки график эмпирической функции, гистограмму и сглаженную гистограмму.

число элементов выборки Х меньших y, N=100.

Интервалы
a0	a1	a2	a3	a4	a5	a6	a7	a8	a9	a10
-2,0511	-1,9565	-1,8619	-1,7672	-1,6726	-1,5780	-1,4834	-1,3888	-1,2942	-1,1996	-1,1050

Таблица для построения гистограммы и эмпирической плотности
	a0 : a1	a1 : a2	a2 : a3	a3 : a4	a4 : a5	a5 : a6	a6 : a7	a7 : a8	a8 : a9	a9 : a10
n	3	4	4	11	12	23	16	18	5	4
h	0,3171	0,4228	0,4228	1,1627	1,2684	2,4311	1,6912	1,9026	0,5285	0,4228
y	-2,0038	-1,9092	-1,8146	-1,7199	-1,6253	-1,5307	-1,4361	-1,3415	-1,2469	-1,1523
y*	-2,4423	-1,9581	-1,4739	-0,9897	-0,5054	-0,0212	0,4630	0,9472	1,4314	1,9156
Ф(y*	0,0202	0,0587	0,1347	0,2445	0,3511	0,3989	0,3584	0,2547	0,1432	0,0637
	0,1035	0,3002	0,6892	1,2512	1,7970	2,0414	1,8343	1,3038	0,7330	0,3260

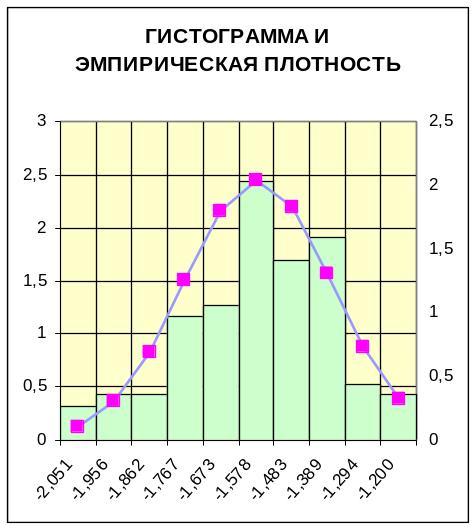
Построим оценки параметров для нормального распределения по методу наибольшего правдоподобия (мнп).

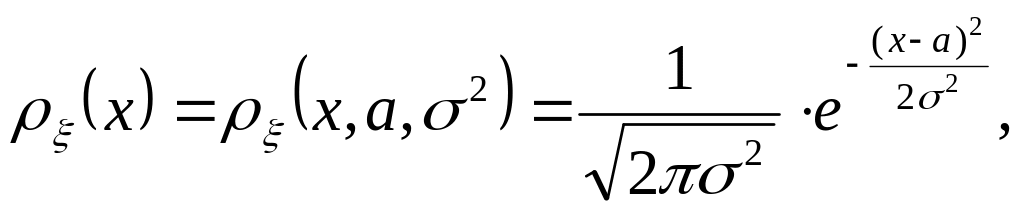
- Неизвестные параметры, - повторная выборка,

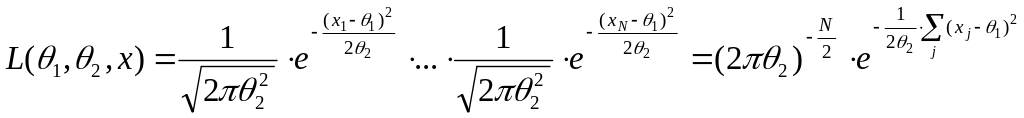Выполняем построение доверительных интервалов.

Перейдем от нормального распределения к стандартному нормальному распределению и найдем С_jиз P(y<C_j)=

Исправленная выборочная дисперсия (S1^2)		Величина C1()
		Величина C1()
		73,3611
0,0386		73,3611
0,0386
		Величина C2()
Функция t(N-1)()		Величина C2()
Функция t(N-1)()		128,4220
1,9842		128,4220
1,9842
		Доверительный интервал для дисперсии (^2)
Доверительный интервал для мат.ожидания (а)

		0,0297	0,0520
-1,5655	-1,4876	0,0297	0,0520

Проверим гипотезу о согласии нормального распределения с имеющимися эмпирическими данными (критерий согласия).

Н₀: F(y) = F₀(y)

p_k= F₀(a_k+1) – F₀(a_k)

Интервалы
a0	a1	a2	a3	a4	a5	a6	a7	a8	a9	a10
-2,051	-1,956	-1,862	-1,767	-1,673	-1,578	-1,483	-1,389	-1,294	-1,200	-1,105

Таблица для построения статистики для проверки ^2-критерия Пирсена (критерия согласия)
	a0 : a1	a1 : a2	a2 : a3	a3 : a4	a4 : a5	a5 : a6	a6 : a7	a7 : a8	a8 : a9	a9 : a10
p	0,045	0,054	0,062	0,068	0,073	0,075	0,075	0,072	0,066	0,059
n	3,000	4,000	4,000	11,000	12,000	23,000	16,000	18,000	5,000	4,000
(n-...	0,525	0,362	0,773	2,523	3,018	31,840	9,718	16,363	0,402	0,624

			Построенная статистика ^2(N)			Величина ^2(r)()
			Построенная статистика ^2(N)			Величина ^2(r)()
			66,1487			15,9872
			66,1487			15,9872

Так как ²(N) >²(r)()то гипотеза Н₀ не верна.

7. Проверим выполнение критерия однородности для объединения двух выборок. Н₀ : F₁(z) = F₂(z)

Интервалы
b0	b1	b2	b3	b4	b5	b6	b7	b8	b9	b10
-2,1105	-1,9935	-1,8764	-1,7593	-1,6423	-1,5252	-1,4082	-1,2911	-1,1740	-1,0570	-0,9399

Таблица числа попаданий элементов выборок в интервалы
	b0 : b1	b1 : b2	b2 : b3	b3 : b4	b4 : b5	b5 : b6	b6 : b7	b7 : b8	b8 : b9	b9 : b10	n.j
n1	1	6	4	15	19	27	19	7	2	0	100
n2	4	4	8	13	17	21	11	11	7	3	99
ni.	5	10	12	28	36	48	30	18	9	3	199

Таблица элементов статистики для проверки гипотезы об однородности
j i	1	2	3	4	5	6	7	8	9	10
1	0,0045	0,0010	0,0033	0,0004	0,0003	0,0019	0,0053	0,0022	0,0069	0,0075
2	0,0044	0,0009	0,0036	0,0003	0,0002	0,0016	0,0050	0,0025	0,0073	0,0077

				Построенная статистика χ^2(2N)			Величина ^2(r-1)
				Построенная статистика χ^2(2N)			Величина ^2(r-1)
				0,00067			14,68366

Так как  ²(2N)<²(r-1)то гипотеза Н₀ верна

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
19.05.20151.47 Mб28методичка.pdf
#
19.05.2015119.81 Кб70Методы изучения педагогического опыта.doc
#
19.05.201575.26 Кб20Методы научного исследовани.doc
#
19.03.201680.26 Кб15методы эконом анализа.docx
#
19.03.2016283.96 Кб19метологические проблемы .rtf
#
29.07.2019536.58 Кб2МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ Рассчётно–графическая работа.doc
#
18.05.2015126.98 Кб10Миф о естественной монополии.doc
#
19.05.20152.27 Mб95МИФВ(251104)А5ЭВ.doc
#
19.05.2015100.86 Кб5Мифы и религия..doc
#
30.09.201951.54 Кб4Мифы о компьютерах.docx
#
22.08.2019218.62 Кб19Младограмматизм.doc

Построим для первой выборки график эмпирической функции, гистограмму и сглаженную гистограмму.

Построим оценки параметров для нормального распределения по методу наибольшего правдоподобия (мнп).