26. Предел и непрерывность функции комплексной переменной.

Пусть однозначная функция определена в некоторой окрестности точки , исключая, может быть, саму точку . Под -окрестностью точки комплексной плоскости понимают внутренность круга радиуса с центром в точке .

Число называется пределом функции в точке (или при 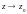), если для любого положительного найдется такое положительное число , что для всех , удовлетворяющих неравенству , выполняется неравенство .

Записывают: .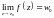

Из определения следует, что если предел существует, то существуют и пределы и .

Пусть функция определена в точке и в некоторой ее окрестности. Функция называется непрерывной в точке , если .

Определение непрерывности можно сформулировать так: функция непрерывна в точке , если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: .

Функция непрерывна в области D, если она непрерывна в каждой точке этой области.

27. Дифференцируемость функций комплексной переменной.

Пусть однозначная функция определена в некоторой окрестности точки , включая и саму точку. Тогда предел 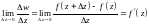, если он существует, называется производной функции в точке , а функция называется дифференцируемой в точке .

28. Аналитическая функция. Условия Коши-Римана.

Однозначная функция называется аналитической в точке , если она дифференцируема (выполнены условия Эйлера-Даламбера) в некоторой окрестности этой точки. Функция называется аналитической в области D, если она дифференцируема в каждой точке .

Теорема Если функция определена в некоторой окрестности точки , причем в этой точке действительные функции и дифференцируемы, то для диффенецируемости функции в точке необходимо и достаточно, чтобы в этой точке выполнялись равенства (Условия Коши-Римана).

29. Гармонические функции. Восстановление аналитической функции по ее действительной или мнимой части.

Дифференциалом аналитической функции в точке называется главная часть ее приращения, т.е. или (так как при будет ). Отсюда следует, что ,т.е. производная функции равна отношению дифференциала функции к дифференциалу независимого переменного. Замечание. Если функция аналитична в некоторой области D, то функции и удовлетворяют дифференциальному уравнению Лапласа( ).

 Действительно, дифференцируя первое из равенств Эйлера-Даламбера по , а второе по , получаем: откуда

Функции и являются гармоническими функциями. 

30. Интеграл от функции комплексной переменной.

Пусть в каждой точке некоторой гладкой кривой L с началом в точке и концом в точке Z определена непрерывная функция .

Разобьем кривую L на n частей (элементарных дуг) в направлении от к точками

В каждой элементарной дуге ( 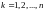) выберем произвольную точку и составим интегральную сумму , где .

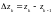Предел такой интегральной суммы при стремлении к 0 длины наибольшей из элементарных дуг, если он существует, называется интегралом от функции по кривой (по контуру) L и обозначается символом .

Таким образом,

31.Теорема Коши для односвязной и многосвязной области.

Теорем (Коши)Если функция аналитична в односвязной области D, то интеграл от этой функции по любому замкнутому контуру L, лежащему в области D, равен 0, т.е.

, т.е. интеграл от аналитической в замкнутой многосвязной области функции по границе области D, проходящей в положительном направлении, равен 0.

32. Интегральная формула Коши.

Теорема Пусть функция аналитична в замкнутой односвязной области и L – граница области D. Тогда имеет место формула 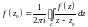, где 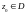- любая точка внутри области D, а интегрирование по контуру L производится в положительном направлении (т.е. против часовой стрелки).

33. Функциональные ряды в комплексной области.

Степенные ряды в комплексной области

Степенным рядом называется ряд

, , ,

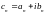Если

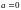
справедлива теорема Абеля.

Если , то данный ряд будет сходиться и в круге и равномерно внутри этого круга.

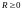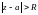Число - называется радиусом сходимости степенного круга - сходится, а при - расходится.

Поскольку по теореме Абеля ряд сходится равномерно , то его можно интегрировать и дифференцировать почленно. Дифференцировать можно бесконечное число раз.

34. Ряд Лорана

Всякая аналитическая в кольце ( ) функция может быть разложена в этом кольце в ряд , коэффициенты которого определяются формулой ( ), где L – произвольная окружность в с центром в точке , лежащая внутри данного кольца.

Ряд Лорана для функции состоит из двух частей. Первая часть ряда Лорана, т.е. ряд называется правильной частью ряда Лорана; этот ряд сходится к аналитической функции внутри круга .

Вторая часть ряда Лорана ,т.е. ряд называется главной частью ряда Лорана; этот ряд сходится в аналитической функции вне круга .