Аналитические методы отыскания оптимального режима объекта управления. Оптимальный одношаговый алгоритм

Название одношаговый он получил потому, что для его работы достаточно знание информации на предыдущем шаге и текущей.

Рассмотрим на примере линейной модели

,

где а_i-оценка i-го параметра модели; N-номер такта или время. Если отсутствует априорная оценка а_i, то на первом шаге она принимается =0. при использовании одношагового алгоритма независимо от своих начальных значений, коэффициенты уточняются по следующей итерационной формуле:

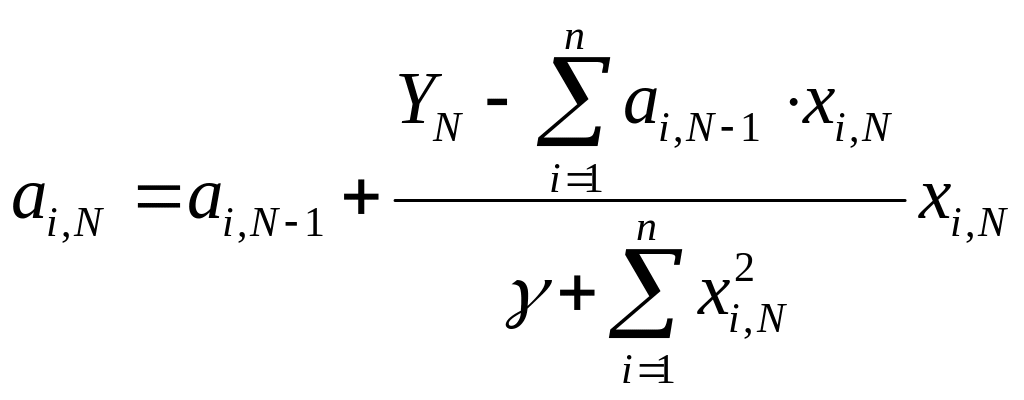(1)

- уточняемый коэффициент на N-ом такте матем.м.

- рассчитанный коэффициент на N-1-ом такте матем.м.

- рассчитанное значение целевой функции Y по коэффициентам а _I из предыдущего такта

- измеренное значение целевой функции на N-ом такте опт.упр.

- сумма квадратов переменных входящих в правую часть мат.модели

- положительный настроечный параметр алгоритма, зависящий от значения ошибок измерения входных и выходных переменных, влияющий на скорость сходимости алгоритма.

Чем > , тем точнее корректируется модель, но меньше скорость сходимости алгоритма.

Из последней формулы видно, что значение числителя характеризует величину разности между действительным значением выходной переменной и значением этой переменной, которое получилось по модели в прошлом такте.

Значение числителя характеризует величину разности между действительным значением выходной переменной Y_N на N-ом такте и значением этой переменной, которая получается по модели с использование параметров а_i,N-1 в прошлом такте.

вводится, когда входные и выходные величины, входящие в целевую функцию измеряются с ошибками.

Скорость сходимости алгоритма определяется числом итераций необходимых для того, чтобы модель из неадекватной стала адекватной.

Пример: Пусть

-- ошибка предсказуемая по мат.модели

Допустим, что х₁ = 3, х₂ = 2, а  = 12 и y_д=50

Тогда

0)

1)

2)

3)

4)

И т.д.

Алгоритм стохастической аппроксимации

Уточнение значения параметров с использованием алгоритма стохастической аппроксимации осуществляется по формуле:

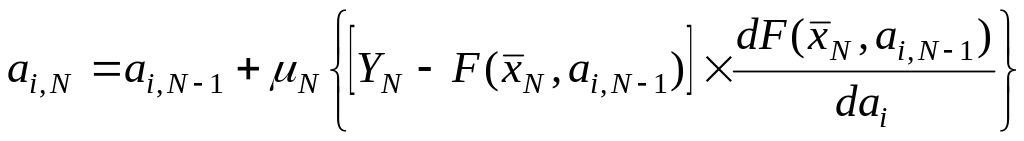
µ_N – настроечный коэффициент, зависящий от номера итерации и обеспечивающий сходимость алгоритма.

µ_{N –} рекомендуют выбирать по следующей формуле:

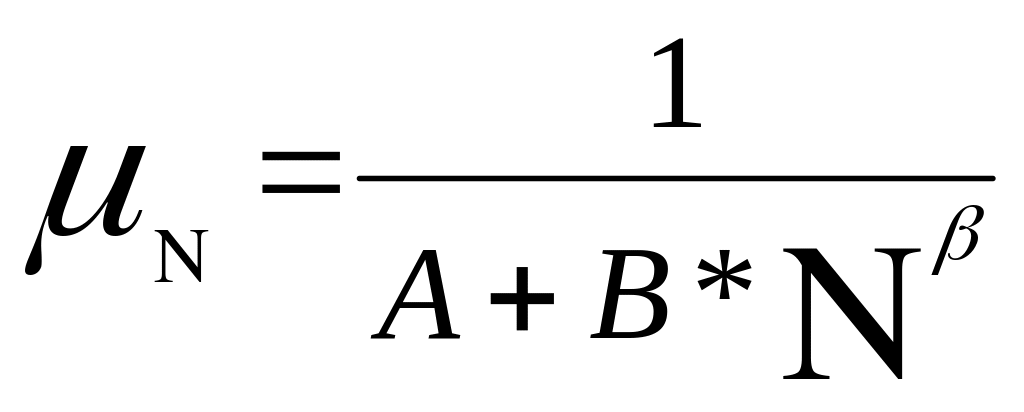А>0, В>0

погрешности измерения неизбежны и наличие случайных помех, входные и выходные координаты x, y делают случайными функциями времени.

Поэтому в математической модели процесса:

x, y – случайные погрешности.

Коэффициент µ делается зависимым от номера итерации т. о, чтобы от шага к шагу влияние случайных погрешностей свести и O.

Y=a₁x₁+a₂x₂

Используя один из алгоритмов, ЭВМ решает задачу построения мат. модели (задачу идентификации), т. е находим коэффициент a₁ и a₂

Этот режим называется режимом обучения.

После обучения следует режим дуального управления (т. е слежение за изменяющимися параметрами объекта и управления по адекватной модели).

a₁ = a₂ =0 Y=0 ( на 0 шаге)

a_1,0 = a₁+ µ₁(Y₁^изм. - 0)* Х₁

a_2,0 = a₂+ µ₁(Y₁^изм. - 0)* Х₂

Y₁=a_1,0x_1,1+a_2,0x_2,1

Y₂=a_1,1x_1,2+a_2,1x_2,2

a_1,1= a_1,0 + µ₂(…….

- ошибка предсказания