3) О трех перпендикулярах.

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной.

И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Доказательство: Пусть АВ - перпендикуляр плоскости , АС - наклонная и с - прямая в плоскости , проходящая через основание С.

Проведем прямую СA1, параллельную прямой АВ. Она перпендикулярна плоскости . Проведем через прямые АВ и СA1 плоскость . Прямая с перпендикулярна прямой СA1. Если она перпендикулярна прямой СВ, то она перпендикулярна плоскости , а значит, и прямой АС.

АНАЛОГИЧНО. Если прямая с перпендикулярна наклонной АС то она, будучи перпендикулярна и прямой СA1 перпендикулярна плоскости , а значит, и проекции наклонной СВ. Теорема доказана.

4)

перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения.

ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ.

Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.

Доказательство.

5) Возможны два случая взаимного расположения двух плоскостей в пространстве:

Параллельны

Пересекаться

Опр. Две плоскости в пространстве называются параллельными, если они не пересекаются, в противном случаи они пересекаются.

Теорема1: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказательство:

Пусть и - данные плоскости, а1 и а2 - прямые в плоскости , пересекающиеся в точке А, в1 и в2 - соответственно параллельные им прямые в

плоскости . Допустим, что плоскости и не параллельны, т.е. пересекаются по некоторой прямой с. По теореме прямые а1 и а2, как параллельные прямым в1и в2, параллельны плоскости , и поэтому они не

пересекают лежащую в этой плоскости прямую с. Таким образом, в плоскости через точку А проходят две прямые (а1 и а2) , параллельные прямой с. Но это невозможно по аксиоме параллельных. Мы пришли к противоречию ЧТД. Параллельность прямой и плоскости

Плоскость α и прямая a, не принадлежащая плоскости α, называются параллельными, если они не имеют ни одной общей точки. Любая прямая a, принадлежащая плоскости α, считается параллельной плоскости α. Если плоскость α и прямая a параллельны, то пишут α∣∣a или

a∣∣α .

Признак параллельности прямой и плоскости:

Если прямая параллельна какой-либо прямой, лежащей в плоскости, то данные прямая и плоскость параллельны.

Теоремы о плоскости и прямой, параллельной плоскости:

Если плоскость проведена через прямую, параллельную другой плоскости, и пересекает эту плоскость, то лилия пересечения плоскостей параллельна данной прямой.

Если через каждую из двух параллельных прямых проведена Произвольная плоскость и эти плоскости пересекаются, то линия их пересечения параллельна каждой из данных прямых.

Параллельность плоскостей. Две плоскости α и β называются параллельными, если они не имеют общей точки и не совпадают. Если плоскости α и β параллельны, то пишут ее α∣∣β .

Свойства параллельных плоскостей:

Любая плоскость считается параллельной самой себе (рефлексивность).

Если плоскость α параллельна плоскости β, то и плоскость β параллельна плоскости α (симметричность).

Если плоскость α параллельна плоскости β, а плоскость β параллельна плоскости γ то плоскость α параллельна плоскости γ (транзитивность).

6) Пусть прямая a является линией пересечения плоскостей α и β (чертеж 3.3.1). Пусть плоскость γ, перпендикулярная прямой a, пересекает плоскости α и β по прямым m и n, которые взаимно перпендикулярны, то есть γ α = m, γ β = n и m n. Такие плоскости α и β называются взаимно перпендикулярными.

Это определение не зависит от плоскости Действительно, если провести другую плоскость перпендикулярную прямой

По теореме о следах. Угол, образованный прямыми и угол, образованный прямыми и равны как углы с соответственно параллельными и одинаково направленными сторонами.

Пусть a α, a β, тогда β α. То есть, если плоскость β содержит прямую a, перпендикулярную плоскости α, то плоскости α и β перпендикулярны. Перпендикулярность прямых - Перпендикулярность плоскостей. Перпендикулярность прямых и плоскостей. c. Перпендикулярные прямые в пространстве. Перпендикулярность прямой и плоскости Перпендикуляр и наклонные Двугранный угол. m. k. Пересекающиеся. Скрещивающиеся. Перпендикулярность прямой и плоскости.

7) 2.Аксиомы стереометрии.

1.Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

2.Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости (прямая лежит в этой плоскости).

Из аксиомы следует, что если прямая имеет не более одной общей точки с плоскостью, то она не принадлежит этой плоскости. Если прямая и плоскость имеют только одну общую точку, то они пересекаются.

3.Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

В этом случае говорят, что плоскости пересекаются по прямой.

На рис. 1 плоскости α и β пересекаются по прямой a.

Записывают это обычно так: α∩β=a.

8) Существуют три случая взаимного расположения двух прямых в пространстве :

прямые лежат в одной плоскости и параллельны;

прямые лежат в одной плоскости и пересекаются;

прямые скрещиваются.

Две прямые называются скрещивающимися , если они не лежат в одной плоскости.

Теорема (признак скрещивающихся прямых):

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.

Доказательство:

Пусть , . Докажем, что и не лежат в одной плоскости. Предположим противное: через прямые a и b проходит некоторая плоскость в . Тогда в проходит через прямую а и точку, не принадлежащую этой прямой, а, значит, совпадает с плоскостью Y . Получили противоречие с условием (прямая ). Значит предположение неверно и прямые a и b скрещивающиеся.

Теорема ( о скрещивающихся прямых ): через каждую из скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

9) 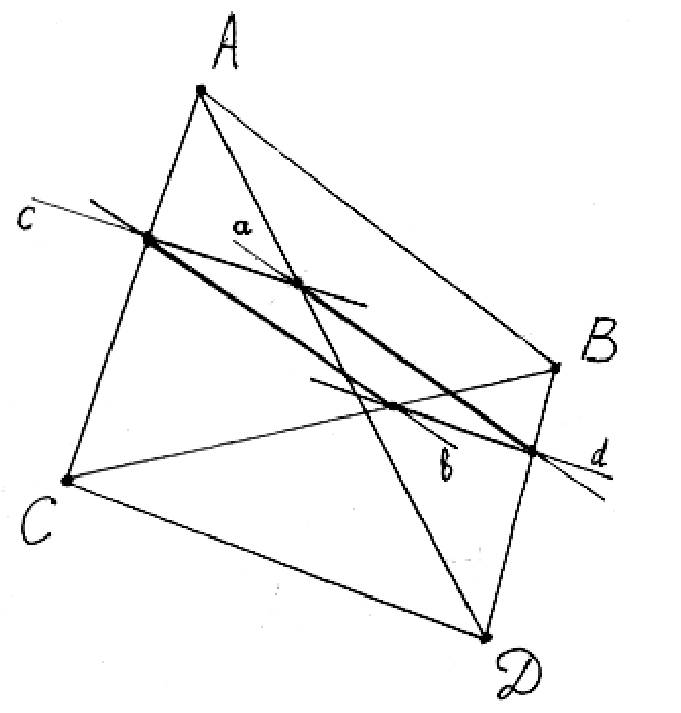Если две прямые пересекаются или параллельны, то они лежат в одной плоскости. Однако в пространстве две прямые могут быть расположены так, что они не лежат в одной плоскости, т. е. не существует такой плоскости, которая проходит через обе эти прямые. Ясно, что такие прямые не пересекаются и не параллельны.

Определение

Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а другая — под эстакадой (рис. 19).

Докажем теорему, которая выражает признак скрещивающихся прямых.

Теорема

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.