15

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»

Кафедра математики

Ен. Ф. 01 математика

МЕТОДИЧЕСКИЕ УКАЗАНИЯ и задания

к лабораторной работе

«Метод наименьших квадратов»

для инженерных специальностей

Уфа 2006

00УДК 51(07)

ББК 22.1я73,22.161.6

М 54

Рекомендовано к изданию методической комиссией факультета механизации сельского хозяйства (протокол № от 2006 года)

Составители: доцент Лукманов Р.Л., ст. преподаватель Гильманова Г.Х.

Рецензент: ст. преподаватель кафедры физики Посняк В.К.

Ответственный за выпуск: зав. кафедрой математики доцент Лукманов Р.Л.

1 Метод наименьших квадратов

Пусть требуется приблизить функцию , заданную таблицей своих значений в точках , в некотором классе функций Например, класс многочленов степени 2 имеет вид Метод наименьших квадратов состоит в таком подборе параметров при котором сумма квадратов отклонений значений функции от в точках минимальна. Другими словами требуется минимизировать функцию многих переменных

Приравняв нулю частные производные функции , получим систему уравнений

(1)

решая которую, можно найти параметры _.

Рассмотрим некоторые частные случаи.

1.1 Линейная модель

Пусть . Тогда , и система (1) примет вид

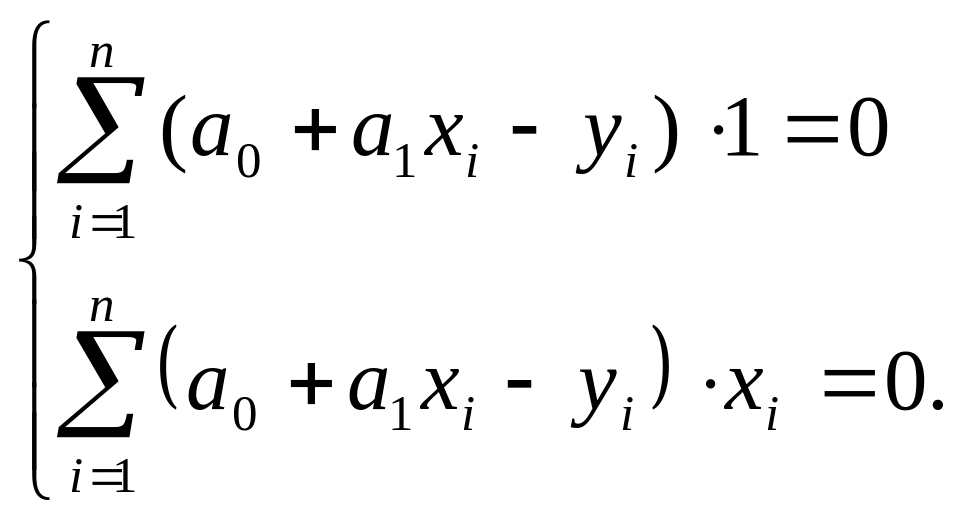
Или после преобразований

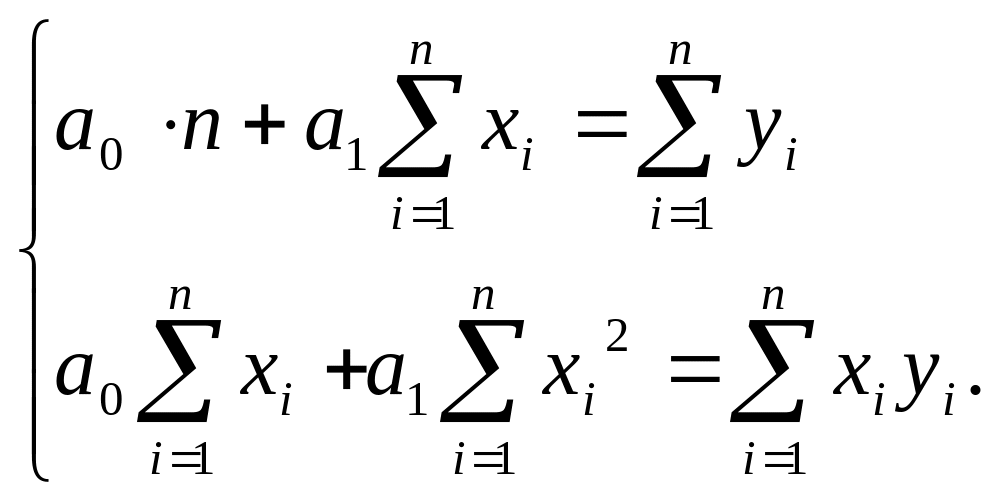(2)

Таким образом, для нахождения коэффициентов получили линейную систему двух уравнений с двумя неизвестными, которую можно записать в виде матричного уравнения

, (3)

где

, , ,

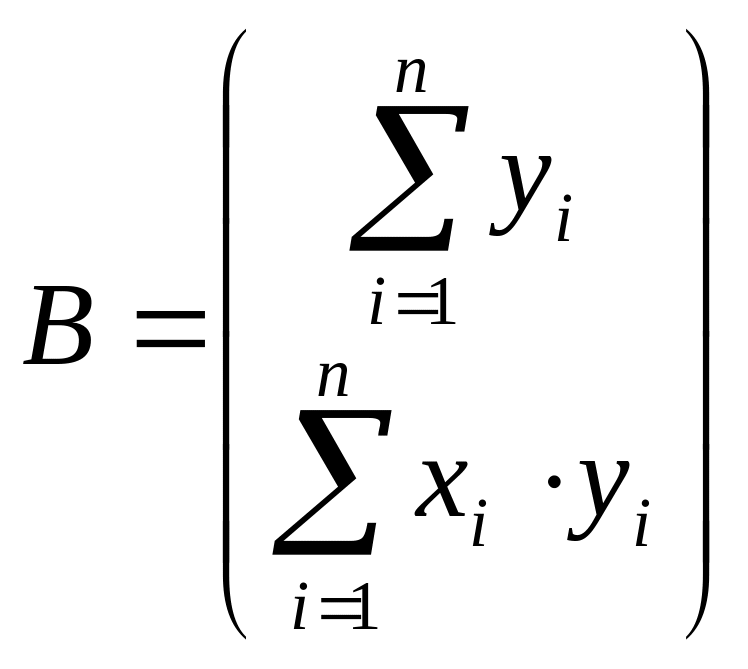решив которую, найдем коэффициенты аппроксимирующей функции .

Проверим правильность работы модели, построив сначала приближающую функцию для точек графика заранее известной функции

Реализация в пакете Mathcad (в фигурных скобках приведены комментарии).

ORIGIN:=1

{ Задаем массивы }

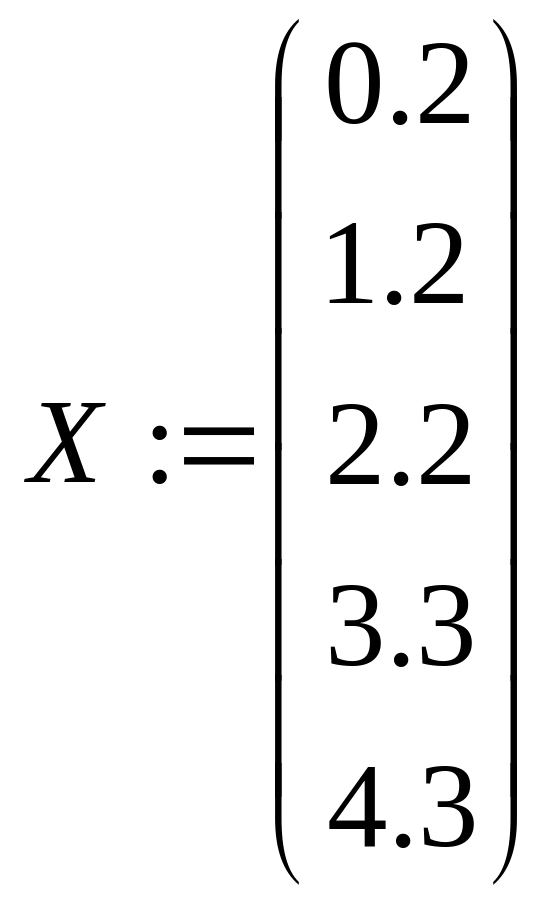
{ Задаем число узлов }

{ Вычислим элементы матриц А и В для системы (2) }

{ Определим матрицы А и В }

{ Решаем матричное уравнение (3) с помощью встроенной процедуры lsolve. Если метод реализован правильно, то решение этого уравнения должно совпадать с коэффициентами функции f(x) }

{ Строим заданные точки и график функции }

{ Вычислим сумму квадратов отклонений }

{ , т.к. точки расположены на одной прямой. В общем случае }

Здесь приведен отладочный вариант программы. Правильность работы программы подтверждается совпадением точек с соответствующими точками графика. При практическом использовании в качестве X и Y вводятся экспериментальные значения.

Пример 1. Для функции, заданной таблицей

х у

0.2 -1

1.2 -0.8

2.2 -0.2

3.3 0.2

4.3 1

построить линейную аппроксимацию методом наименьших квадратов.

При решении этой задачи в приведенной выше программе в качестве Х и У вводятся заданные табличные значения. Аппроксимирующее линейное приближение имеет вид , График приближающей функции и исходные точки изображены на рисунке 1:

Рисунок 1