Питання державної атестації с математики для студентів першого курсу всіх спеціальностей.

Білет №1

1. Функція y=sin x, її графік і властивості.

Властивості:

1. Область визначення - проміжок (-∞;+∞).

2. Область значень – проміжок [-1;1].

3. Функція непарна, періодична з періодом Т=2П.

4. Функція зростає при -П/2+2Пn<х<П/2+2Пn, n є Z.

5. Функція спадає при П/2+2Пn<х<3П/2+2Пn, n є Z.

6. Функція має максимум у точках (П/2+2Пn;0), мінімум у точках (-П/2+2Пn;0), nє Z.

2. Призма. Паралелепіпед. Їх елементи та властивості.

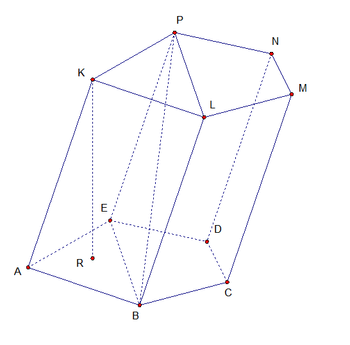
Призма - багатогранник, дві грані якого є рівними багатокутниками, що лежать в рівнобіжних площинах, а інші грані - параллелограммами, що мають загальні сторони з цими багатокутниками. Або (рівносильно) - це багатогранник, в основі якого лежать рівні багатокутники, а бічні грані - паралелограми.

Таблиця елементів призми.

Назва	Визначення	Позначення на кресленні	Креслення
Підстави	Дві грані, які є конгруентні багатокутниками, що лежать в рівнобіжних площинах.	ABCDE, KLMNP
Бічні грані	Всі грані, крім підстав. Кожна бічну грань обов'язково є паралелограмом.	ABLK, BCML, CDNM, DEPN, EAKP
Бічна поверхня	Об'єднання бічних граней.
Повна поверхня	Об'єднання підстав і бічній поверхні.
Бічні ребра	Загальні сторони бічних граней.	AK, BL, CM, DN, EP
Висота	Відрізок, що сполучає підстави призми і перпендикулярний ім.	KR
Діагональ	Відрізок, що сполучає дві вершини призми, що не належать одній межі.	BP
Діагональна площина	Площина, що проходить через бічне ребро призми і діагональ підстави.
Діагональний переріз	Перетин призми і діагональної площині. У перетині утворюється паралелограм, у тому числі його окремі випадки - ромб, прямокутник, квадрат.	EBLP
Перпендикулярний переріз	Перетин призми і площини, перпендикулярної її бічного ребру.

Властивості призми:

• Підстави призми є рівними багатокутниками.

• Бічні грані призми є параллелограммами.

• Бічні ребра призми паралельні і рівні.

• Обсяг призми дорівнює добутку її висоти на площа основи:

• 

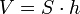
• Площа повної поверхні призми дорівнює сумі площі її бічній поверхні і подвоєною площі підстави.

• Площа бічній поверхні довільної призми 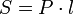, де P - периметр перпендикулярного перетину, l - довжина бічного ребра.

• Перпендикулярний переріз перпендикулярно до всіх бічних ребрах призми.

• Кути перпендикулярного перетину - це лінійні кути двугранних кутів при відповідних бічних ребрах.

• Перпендикулярний переріз перпендикулярно до всіх бічних граней.

Паралелепіпед - призма, основою якої є паралелограм, або багатогранник, у якого шість граней і кожна з них паралелограм.