Сущность регрессионного анализа

Основной характеристикой вероятностной связи между случайной величиной у и неслучайной х является регрессия, т.е. зависимость математического ожидания (среднего значения) случайной величины у от x. График этой зависимости называется линией регрессии.

Регрессионный анализ - это нахождение зависимости по отдельным значениям величины (обычно по экспериментальным точкам). Линейная зависимость между величинами, или их логарифмами является наиболее распространенной. Уравнение линии регрессии записывают в виде

m_y=₀+x ,

где  , ₀ -параметры или коэффициенты регрессии.

Оценкой линии регрессии является эмпирическая линия регрессии, уравнение которой имеет вид

где ,b , b₀ - оценки величин m_у , , ₀ соответственно.

Коэффициенты регрессии b и b₀ находят методом наименьших квадратов, в основу которого положено требование минимизации квадратов отклонений результатов измерений от линии регрессии. На основе решения системы уравнений можно получить формулы для коэффициентов b и b₀:

, .

Методика обработки результатов испытаний

В данном задании рассматривается изменение удельного расхода топлива С_УД по наработке. В табл.4.1 приведены статистические данные изменения С_УД по наработке .

Изменение удельного расхода топлива от наработки не является линейным и поэтому описывается степенной зависимостью:

,

где С_УД - изменение удельного расхода топлива; А и b - искомые коэффициенты регрессионной зависимости.

Логарифмируя данные уравнения, получим:

Уравнение эмпирической линии регрессии представляем в виде: ,

где - оценка математического ожидания логарифма удельного расхода топлива; Х= lg - логарифм времени наработки; lgA, b - коэффициенты, подлежащие определению.

Изменение удельного расхода топлива двигателей по наработке

Таблица 4.1

Номер двиг.		СR	lg	lgСR	Номер двиг.		СR	lg	lgСR
1	1000	4	3	0.6021	28	3000	0	3.4771	0
2	1000	6	3	0.7781	29	3011	11	3.4787	1.0414
3	1000	5	3	0.6990	30	3016	10	3.4794	1
4	1010	0	3.0043	0	31	3074	2	3.4877	0.3010
5	1250	5	3.0969	0.6990	32	3214	6	3.5070	0.7781
6	1250	5	3.0969	0.6990	33	3255	18	3.5125	1.2553
7	1500	5	3.1761	0.6990	34	3301	9	3.5186	0.9542
8	1527	0	3.1838	0	35	4000	8	3.6021	0.9031
9	1706	7	3.2320	0.8451	36	4527	11	3.6558	1.0414
10	1750	6	3.2430	0.7781	37	4710	11	3.6730	1.0414
11	1750	0	3.2430	0	38	4744	10	3.6761	1
12	1808	11	3.2572	1.0414	39	4994	-	3.6984	0
13	1880	16	3.2742	1.2041	40	5000	11	3.6989	1.0414
14	1940	3	3.2878	0.4771	41	5000	16	3.6989	1.2041
15	2000	4	3.3010	0.6021	42	5000	-	3.6989	0
16	2000	8	3.3010	0.9031	43	5253	16	3.7204	1.2041
17	2000	12	3.3010	1.0792	44	6000	13	3.7781	1.1139
18	2000	13	3.3010	1.0139	45	6145	13	3.7885	1.1139
19	2000	15	3.3010	1.1761	46	6149	19	3.7888	1.2787
20	2000	8	3.3010	0.9031	47	6535	26	3.8152	1.4150
21	2006	10	3.3023	1	48	7400	24	3.8692	1.3802
22	2020	3	3.3053	0.4771	49	8004	28	3.9033	1.4472
23	2385	5	3.3775	0.6990	50	8004	4	3.9055	0.6021
24	2400	7	3.3802	0.8451	51	7981	24	3.9021	1.3802
25	2817	-	3.4498	0	52	7993	19	3.9027	1.2787
26	2880	15	3.4594	1.1761	53	7998	13	3.9029	1.1139
27	3000	6	3.4771	0.7781	54	7079	19	3.8499	1.2787
					55	2817	4	3.4500	0.6021

Определяем коэффициенты b и b₀:

,

Рассеяние значений относительно линии регрессии оцениваем средним квадратичным отклонением:

.

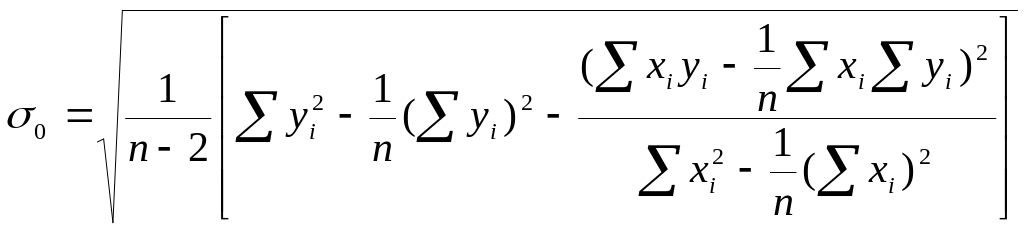Полагая, что распределение случайной величины описывается нормальным распределением, получаем зависимость между случайной величиной C_R и неслучайной величиной :

где Ф(z) - табулированная нормированная величина распределения по нормальному закону с параметрами m = 0 и  = 1. Блок-схема расчета параметрической надежности приведена в приложении.

Порядок проведения задания:

1. Ознакомиться c теоретическими основами построения регрессионной зависимости.

2. По данным испытаний (табл.4.1) определить коэффициенты регрессии и среднеквадратическое отклонение значений измерений.

3. Построить график регрессионной зависимости удельного расхода топлива C_R от наработки .

Содержание отчета практического занятия №4:

1. Описание метода регрессионного анализа.

2. Таблица исходных данных.

3. Расчетные значения коэффициентов регрессии.

4. График регрессионной зависимости: lgC_R=b₀ lg_+b₀ .