
Практическое занятие №8 Усложненные задачи транспортного типа.
На практике классические задачи транспортного типа встречаются крайне редко. Обычно при составлении экономико-математической модели задачи транспортного типа приходится вводить целый ряд дополнительных ограничений, а затем пользоваться методом потенциалов. Ряд экономических задач легко сводим к транспортной задаче. Рассмотрим наиболее часто встречающиеся ситуации.
Отдельные поставки от определенных поставщиков некоторым потребителям должны быть исключены (из-за отсутствия необходимых условий хранения, чрезмерной перегрузки коммуникаций и т. д.). Это ограничение требует, чтобы в матрице перевозок, содержащей оптимальный план, определенные клетки оставались свободными. Последнее достигается искусственным завышением затрат на перевозки Сij в клетках, перевозки через которые следует запретить. При этом производят завышение величины Сij до таких значений, которые будут заведомо больше всех, с которыми их придется сравнивать в процессе решения задачи.
На предприятии необходимо определить минимальные суммарные затраты на производство и транспортировку продукции. C подобной задачей сталкиваются при решении вопросов, связанных с оптимальным размещением производственных объектов. Экономически более выгодной может оказаться доставка сырья из более отдаленных пунктов, но при меньшей его себестоимости. В таких задачах за критерий оптимальности принимают сумму затрат на производство и транспортировку продукции.
Ряд транспортных маршрутов по которым необходимо доставить грузы, имеет ограничения по пропускной способности. Если, например, по маршруту A1B1 можно провести не более q единиц груза, то Bj столбец матрицы разбивается на два Вj` и Bj``. В первом спрос принимается равным разности между действительным спросом bj и ограничением q: bj` = bj — q, во втором - равным ограничению q, т. е. b'`j= q. Затраты Сij в обоих столбцах одинаковы и равны данным, но в первом столбце B`j, в клетке, соответствующей ограничению i, вместо истинного тарифа Сij ставится искусственно завышенный тариф, т.е. ставится число на порядок большее остальных чисел (клетка блокируется). Затем задача решается обычным способом.
Поставки по определенным маршрутам обязательны и должны войти в оптимальный план независимо от того, выгодно это или нет. В этом случае уменьшают запас груза у поставщиков и спрос потребителей и решают задачу относительно тех поставок, которые необязательны. Полученное решение корректируют с учетом oбязательных поставок.
Экономическая задача не является транспортной, но в математическом отношении подобна транспортной, так как описывается аналогичной моделью. Например, распределение производства изделий между предприятиями, оптимальное закрепление механизмов по определенным видам работы.
Необходимо максимизировать целевую функцию задачи транспортного типа. В этой ситуации при составлении опорного плана в первую очередь стараются заполнить клетки с наиболее высокими значениями показателей Сij. Выбор клетки, подлежащей заполнению при переходе oт одного допустимого плана к другому, должны производиться не по минимальной отрицательной разнице [сij - (αi + βj)], а по максимальной положительной разнице. Оптимальным будет план, которому в последней таблице сопутствуют свободные клетки с неположительными элементами: все разности [сij - (αi + βj)]≤0
Необходимо в одно время распределить груз различного рода по потребителям. Задачи данного типа называются мнoгопродуктовыми транспортными задачами. В этих задачах поставщики т родов грузов разбиваются на условных поставщиков, а потребители n родов грузов разбиваются на n условных потребителей. С учетом этой разбивки составляют полную транспортную таблицу. При этом заметим, что некоторые маршруты AiBj должны быть блокированы (закрыты), поскольку в данной постановке задачи грузы разного рода не могут заменять друг друга. Этим маршрутам должна соответствовать очень высокая стоимость перевозки. Многопродуктовую задачу не всегда обязательно описывать одной моделью, Например, если поставки грузов различного рода независимы, то задачу можно представить в виде комплекса транспортных задач по каждому роду груза. Однако если между грузами различного рода существует связь (например, одни из грузов можно заменить другими), то в общем случае исходную модель (задачу) не удается разбить на комплекс простых транспортных задач.
Доставка груза в кратчайший срок
В практической деятельности могут возникнуть ситуации, когда нас в первую очередь интересуют не затраты на перевозку груза (их минимизация), а время доставки этих грузов потребителям. Например, при подготовке крупных военных операций необходимо в кратчайший срок сосредоточить ресурсы в намеченных пунктах или при стихийных бедствиях (землетрясение, ураганы и т. п.) возникает задача обеспечения пострадавших районов различными ресурсами в кратчайший срок.
Для решения подобных задач рассмотренный ранее метод потенциалов непригоден. Эти задачи решаются с помощью специального алгоритма.
Составить матрицу условий так как это делают при решении обычной транспортной задачи.
Найти методом потенциалов план, у которого линейная форма
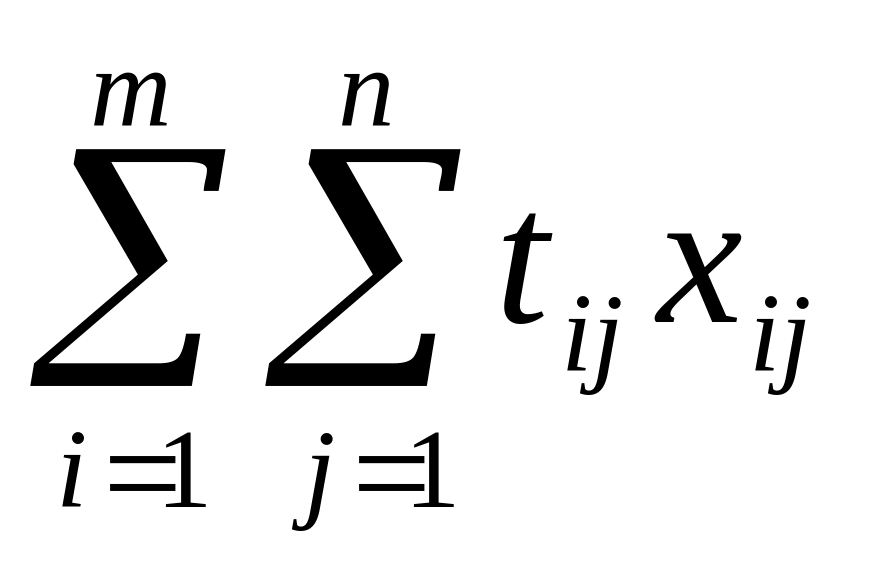 достигает
минимального значения.
достигает
минимального значения.Определить max tij (наибольшее из времён) запланированных перевозок (где хij > 0 ).
Заблокировать все всех клетки матрицы, где tij ≥ max t`ij.
Отыскать для изменённой матрицы решение, при котором линейная форма
 достигает минимума. Если в полученном
решении хij
> 0
расположены только в незаблокированных
клетках, то снова находим max
t``ij
и повторяем шаги 4 и 5. Если же в полученном
решении имеется хотя бы один xij
> 0 расположенный в заблокированной
клетке, то оптимальным будет предыдущее
решение.
достигает минимума. Если в полученном
решении хij
> 0
расположены только в незаблокированных
клетках, то снова находим max
t``ij
и повторяем шаги 4 и 5. Если же в полученном
решении имеется хотя бы один xij
> 0 расположенный в заблокированной
клетке, то оптимальным будет предыдущее
решение.
Очевидно, что после конечного числа повторений шагов 3, 4 и 5 будет получено оптимальное решение, т.е. такой план перевозок, по которому грузы всем потребителям будут доставлены за возможно короткое время.
