Вопросы к экзамену по линейной алгебре

1. Определители второго порядка. Решение системы линейных уравнений 2х2 при их помощи. Пример.

a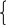 x+by=c a,b,d,e – коэффициенты системы

dx+ey=f c,f – свободные члены

Определителем 2 порядка называется число, которое составляется из 4х упорядоченных чисел по следующему правилу:

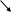
∆ = a b = ae - bd

d e

∆ = 2 -1 = 2*(-2) – (-1)*3 = -4 + 3= -1

3 -2

Обозначим через ∆х – определитель 2 порядка, который получается из главного определителя системы ∆ заменой столбца коэффициентов при неизвестном х столбом свободных членов.

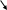
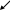∆ х = c b

f e

а налогично, ∆у = a c

d f

ТЕОРЕМА

Если главный определитель системы ∆ ≠ 0, то система имеет единственное решение следующего вида:

х = ∆х

х

у = ∆у

у

2. Определитель 3 порядка. Определение, примеры.

a ₁₁x₁ + a₁₂x₂ + a₁₃x₃ = b₁

a₂₁x₁ + a₂₂x₂ + a₂₃x₃ = b₂

a₃₁x₁ + a₃₂x₂ + a₃₃x₃ = b₃

Главным определителем 3 порядка называется число ∆, которое составляется из 9 упорядоченных чисел по следующему правилу:

∆ = а₁₁ а₁₂ а₁₃ 0 0 0 0 0 0

а₂₁ а₂₂ а_{23 главная диагональ} 0 0 0 0 0 0

а₃₁ а₃₂ а₃₃ 0 0 0 0 0 0

_{побочная диагональ} «+» «-»

ТЕОРЕМА КРАМЕРА

Если главный определитель системы ∆ ≠ 0, то система имеет единственное решение, определяемое формулами:

х1 = ∆1

∆

х2 = ∆2

∆

х3 = ∆3

∆

3. Свойства определителя 3 порядка, примеры.

Определитель – число, которое состоит из 9 чисел, записанное в виде таблички

∆ = а₁₁ а₁₂ а₁₃ строка, а - элемент

а₂₁ а₂₂ а₂₃

а₃₁ а₃₂ а₃₃

столбец

Все сформулированные ниже свойства проверяются по определению определителя:

1. Определитель не изменится, если все строки заменить соответствующими столбцами

2. Если определитель содержит строку (столбец) еликом состоящий из нулей, то он = 0

3. Определитель с двумя пропорциональными строками (столбцами) равен 0

4. Общий множитель некоторой строки (столбца) можно выносить за знак определителя

∆ = к*а₁₁ к*а₁₂ к*а₁₃ = а₁₁ а₁₂ а₁₃

а₂₁ а₂₂ а₂₃ к* а₂₁ а₂₂ а₂₃

а₃₁ а₃₂ а₃₃ а₃₁ а₃₂ а₃₃

5. Величина определителя не изменится, если к элементам некоторой его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженное на одно и то же число

_{+(2*а21) +(2*а22) +(2*а23)}

∆ = а₁₁ а₁₂ а₁₃

2*а₂₁ 2*а₂₂ 2*а₂₃

а₃₁ а₃₂ а₃₃