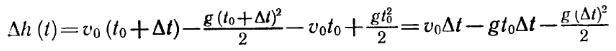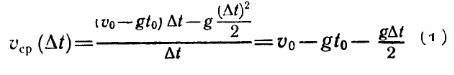Средняя скорость
Сре́дняя ско́рость — в кинематике некая усреднённая характеристика скорости частицы за время её движения. Различают два основных определения средней скорости.
Средняя (путевая) скорость— это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:
![]()
Средняя путевая скорость, в отличие от мгновенной скорости не является векторной величиной.
Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени.
В то же время если, например, половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч. В примерах, подобных этому, средняя скорость равна среднему гармоническому всех [скоростей на отдельных, равных между собой, участках пути.
Средняя скорость по перемещению
Можно также ввести среднюю скорость по перемещению, которая будет вектором, равным отношению перемещения ко времени, за которое оно совершено:
![]()
Средняя скорость, определённая таким образом, может равняться нулю даже в том случае, если точка (тело) реально двигалась (но в конце промежутка времени вернулась в исходное положение).
Если перемещение происходило по прямой (причём в одном направлении), то средняя путевая скорость равна модулю средней скорости по перемещению.
Мгновенная скорость.
|