19. Соединение обмоток генератора в звезду и треугольник.

Соединение обмоток генератора звездой

При соединении обмоток генератора звездой концы обмоток X, Y и Z электрически соединяются в одну точку 0 (рис. 16.3а), кото­рая называется нулевой, или нейтральной. При этом генератор с потребителем соединяется тремя или четырьмя проводами.

Провода, подключенные к началам обмоток генератора (А, В и Q, называют линейными проводами, а провод, подключенный к нулевой точке 0, называется нулевым, или нейтральным.

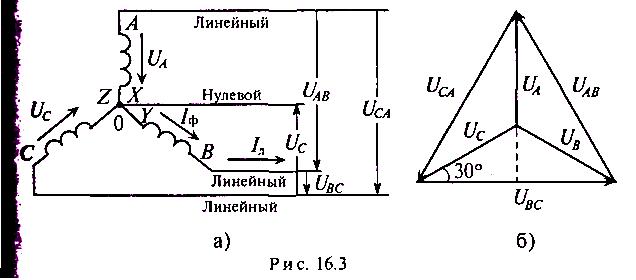
В связанных трехфазных системах различают фазные и линей­ные напряжения и токи.

Фазным называется напряжение между началом и концом обмотки генератора или между нулевым и линейным проводом. Обознача­ется фазные напряжения прописными буквами с индексами фаз U_A, Uв, U_c (рис. 16.3а). Так как сопротивление обмоток генератора мало, то фазные напряжения практически не отличаются от ЭДС в обмотках генератора.

Линейным называется напряжение между началами обмоток генератора или между линейными проводами. Обозначаются линейные Спряжения U_AB, U_BC, U_CA (рис. 16.3а).

Можно определить зависимость между линейными и фазными напряжениями при соединении обмоток генератора звездой.

Мгновенные значения фазных напряжений равны разностям потенциалов между началами и концами соответствующих обм0! ток, т. е.

(16.5)

Мгновенные значения линейных напряжений равны разностям потенциалов между началами соответствующих обмоток:

(16.6)

Потенциалы концов обмоток одинаковы φ_X= φ_у= φz, так как все они соединены электрически в одну точку. Тогда

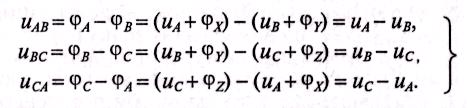(16.7)

То есть мгновенное значение линейных напряжений определя­ется разностью мгновенных значений двух соответствующих фаз­ных напряжений.

При соединении обмоток генератора звездой действующее значе­ние линейного напряжения определяется геометрической разностью двух соответствующих фазных напряжений. На этом основании построена векторная диаграмма напряжений (рис. 16.36) для сое­динения обмоток генератора звездой. К такому же результату приводит определение комплексов линейных напряжений симво­лическим методом:

(16.8)

При симметричной системе ЭДС фазные напряжения равны по величи­не (U_А = Uв = Uc) и сдвинуты по фазе на угол 120°. По векторной диаграмм (рис. 16.36) определяется линейное на­пряжение (рис. 16.4).

Л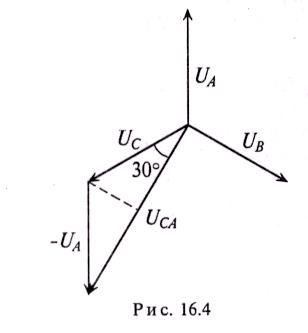 инейное напряжение U_СА при сим­метричной системе ЭДС трехфазного генератора определяется равенством

Из диаграммы (рис. 16.4) определяется вектор (комплекс)U_CА-

Прu симметричной системе ЭДС линейное напряжение трехфаз­ного генератора, обмотки которого соединены звездой, в √3= 1,73 раза больше фазного напряжения:

(16.9)

Если говорят о напряжении генератора 127/220 В, то имеется в виду, что фазное напряжение в трехфазной цепи 127 В, а линей­ное - 220 В. В сети с напряжением 220/380 В фазное напряжение 220 В, а линейное — 380 В. Очевидно, что обмотки генератора та­кой симметричной цепи соединены звездой и отношение напря­жений получится равным

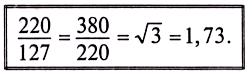(16.10)

В связанных трехфазных системах фазным называется ток, про­ходящий по обмотке (фазе) генератора I_ф, а линейным считается ток, проходящий по линейному проводу I_π.

Как видно на рис. 16.3а, при соединении обмоток генератора звездой линейный ток I_л равен фазному току I_ф: (16.11)

Соединение обмоток генератора треугольником

При соединении обмоток генератора треугольником (рис. 16.5а) конец обмотки фазы А соединяется с началом обмотки фазы В, конец обмотки фазы В соединяется к началом обмотки фазы С, конец обмотки фазы С соединяется с началом обмотки фазы А и к точкам соединения подключаются линейные провода.

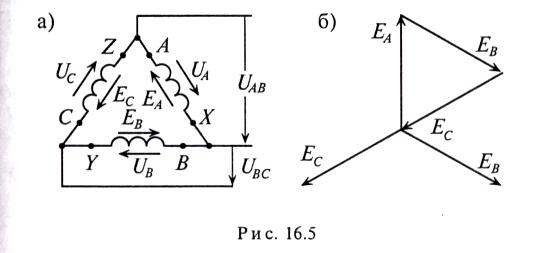
При соединении обмоток генератора треугольником (рис. 16.5a) трехфазная цепь трехпроводная.

Как следует из схемы соединения обмоток треугольников (рис. 16.5а), линейное напряжение U_AB равно фазному напряже­нию U_А, U_BC= U_B и U_CA= U_c.

То есть _{(16 12)}

Из схемы (рис. 16.5а) следует, что три обмотки генератора, сое­диненные треугольником, образуют замкнутый контур, ток в ко­тором при отсутствии нагрузки (холостой ход) определяется вы­ражением

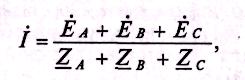(16.13)

где Е_а, Ев и Е_С — комплексы (векторы) ЭДС фаз генератора; Za, Zb и Zc — комплексы сопротивлений обмоток генератора (Z_a = R_A +jX_A; Zb = Rв + jX_B и Zc= R_c+jX_c), т. е. каждая обмотка об­ладает активным R и индуктивным X сопротивлениями.

Так как сопротивления обмоток малы, падением напряжения на них можно пренебречь и считать, что напряжение на каждой об­мотке генератора равно ее ЭДС.

При симметричной системе ЭДС и правильном соединении об­моток генератора треугольником (рис. 16.5а) геометрическая сумма ЭДС (комплексов) обмоток генератора, образующих зам­кнутый контур, равна нулю (рис. 16.56). Следовательно, и ток в замкнутом контуре обмоток, соединенных треугольником, также равен нулю (/=0) при холостом ходе независимо от величины внутреннего сопротивления обмоток Z

Если обмотки симметричного генератора соединены «непра­вильным» треугольником, т. е. неправильно подключить начало и конец хотя бы одной из обмоток, например BY (рис. 16.5'а), то геометрическая сумма ЭДС в замкнутом контуре обмоток будет равна удвоенному значению ЭДС одной фазы (рис. 16.5'б). С уче­том малого внутреннего сопротивления обмоток генератора ток в

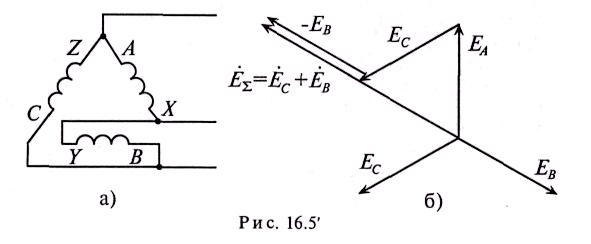
замкнутом контуре достигает катастрофической величины даже при отсутствии нагрузки (холостой ход). Таким образом, соединение обмоток трехфазного генератора «неправильным» треугольником равносильно короткому замыканию в замкнутом контуре обмоток .

20. Расчёт симметричной трёхфазной цепи в звезду.

21. Расчёт симметричной трёхфазной цепи в треугольник.

22. Расчёт несимметричной трёхфазной цепи в треугольник.

23. Расчёт несимметричной трёхфазной цепи в звезду.