7. Задача оптимизации процессов управления

8. Постановка транспортной задачи и ее математическая модель.

Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. В общей постановке транспортная задача состоит в отыскании оптимального плана перевозок некоторого однородного груза с m баз A1,A2,…Am n потребителям B1,B2,…Bn, не превышающий объем производства в каждом пункте поставки. Математическая формулировка транспортной задачи такова: найти переменные задачи 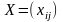, i=1,2,,…,m, j=1,2,…,n, удовлетворяющие системе ограничений (2), (3), условиям неотрицательности (4) и обеспечивающие минимум целевой функции (1).

В данном методе запасы очередного поставщика используются для обеспечения запросов очередных потребителей до тех пор, пока не будут исчерпаны полностью, после чего используются запасы следующего по номеру поставщика.

Заполнение таблицы транспортной задачи начинается с левого верхнего угла и состоит из ряда однотипных шагов. На каждом шаге, исходя из запасов очередного поставщика и запросов очередного потребителя, заполняется только одна клетка и соответственно исключается из рассмотрения один поставщик или потребитель.

Метод минимальной стоимости прост, он позволяет построить опорное решение, достаточно близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи С=(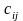 ), i=1,2,,…,m, j=1,2,…,n. Как и метод северо-западного угла, он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости min { }, и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Очередную клетку, соответствующую , заполняют по тем же правилам, что и в методе северо-западного угла. Поставщик исключается из рассмотрения, если его запасы использованы полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от данного поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь, затем поставщик исключается из рассмотрения. Аналогично с потребителем.

9. Методика решения транспортных задач методом потенциалов.

10. Транспортная задача определения оптимального плана перевозок.

При некотрых реальных условиях перевозки груза из определенного пункта в пункт назначения не могут быть осуществлены. Для определения оптимальных планов таких задач предполагают, что стоимость перевозки единицы груза из пункта в пункт является сколь угодно большой величиной М и при этом условии известными методами находят решение транспортной задачи. Такой подход к нахождению решения ТЗ называется запрещением перевозок.

2. В отдельных ТЗ дополнительным условием является обеспечение перевозки по соответствующим маршрутам определенного количества груза. Пусть, например, из в требуется обязательно перевезти единиц груза. Тогда в соответствующую клетку таблицы, находящуюся на пересечении строки и столбца , записывают указанное число и в дальнейшем считают эту клетку свободной со сколь угодно большой стоимостью перевозки М. Для полученной таким образом новой транспортной задачи находят оптимальный план, который определяет оптимальный план исходной задачи.

3. Иногда требуется найти решение ТЗ, при котором из в должно быть перевезено не менее заданного количества груза . Для определения оптимального плана такой задачи считают, что запасы и потребности меньше фактических на единиц. После этого находят оптимальный план новой ТЗ, на основании которого и определяют решение исходной задачи.