Лаб. раб.№7

Лабораторная работа № 7 измерение индукции магнитного поля катушки

Приборы и оборудование: магнит, подвешенный на нити;

катушка—соленоид; амперметр {с пределом измерения до 1 А};

реостат {сопротивление R= 30 ом, I = 2 А};

источник напряжения /аккумулятор/;

коммутатор;

секундомер.

ВВЕДЕНИЕ

Для характеристики магнитного поля введен вектор магнитной индукции B, который можно определить из формулы Ампера:

/1/

— сила, действующая со стороны внешнего магнитного поля на проводник l с током I, — угол между векторами индукции и током.

За единицу индукции магнитного поля в системе СИ принимается 1 Н/А*м , т.е. индукция такого однородного поля, в котором на прямой проводник в 1 м и с током в 1 А, расположенный перпендикулярно к магнитному полю действует сила в 1 H. Эта единица имеет название В*с/м² или Вб/м² . Если в однородном магнитном поле находится некоторый контур тока, площадь которого S, то на контур будет действовать пара сил, максимальный момент которой равен:

/2/

Величина является характеристикой контура и называется вектором магнитного момента контура с током. Вектор направлен нормально к площадке и образует с направлением тока право-винтовую систему. Заменяя в формуле /2/ получим:

/3/

В общем случае величина момента пары сил равна:

/4/

где — угол между векторами и .

Приведенное определение используется для постоянного магнита, который обладает остаточным магнитным моментом.

Если такой магнит, подвешенный на нити так, чтобы он мог вращаться около вертикальной оси, проходящей через центр тяжести, поместить в магнитное поле, то на него будет действовать лишь горизонтальная составляющая вектора индукции . В этом случае, направление магнитного момента Р будет совпадать с горизонтальной составляющей индукции магнитного поля . Такой магнит будучи повернут относительно вращения на некоторый угол /угол между направлениями и / в дальнейшем будет совершать крутильные колебания /рис.1/. Для малых углов /менее 6°/ sin = , период колебания рассчитывается по формуле крутильных колебаний:

/5/

где — момент инерции магнита.

А при этих условиях , то тогда:

/6/

Эта формула используется в работе для определения индукции магнитного поля соленоида.

Соленоид /рис.1/ представляет систему одинаковых круговых токов с общей прямой осью. Таким образом, соленоидом называют катушку индуктивности, по которой пропускается ток. В любой точке внутри соленоида вектор индукции магнитного поля В параллельно оси соленоида АВ. Для расчета магнитных полей, созданных токами используется закон полного тока: циркуляция вектора индукции магнитного поля вдоль любого замкнутого контура равна алгебраической сумме токов, охватываемых контуром:

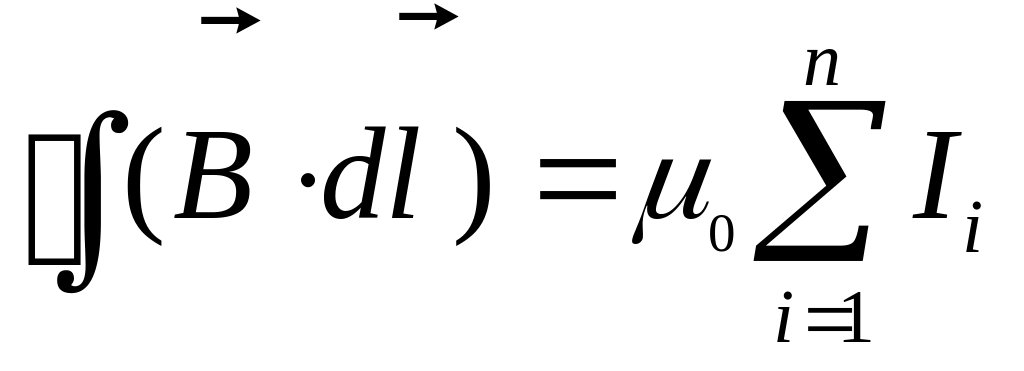/7/

Токи остаются положительными, если из конца вектора плотности тока обход контура кажется происходящим против часовой стрелки. Токи, которые не охватываются контуром, не дают вклада в циркуляцию Произведем расчет магнитного поля соленоида.

Циркуляция вектора В по прямоугольному контуру АВСД равна:

При обходе по часовой стрелке /рис. / направление вектора совпадает с вектором AB; BC и AD перпендикулярны вектору .

Участок контура ДС может быть взят на очень большом расстоянии от соленоида, где полем можно пренебречь / = 0/. Тогда, циркуляция индукции В по замкнутому контуру АВСД равна:

/8/

По закону полного тока эта циркуляция индукции В должна быть равна сумме токов, охватываемых контуром АBСД.

где — ток в соленоиде, — число витков, — длина соленоида, — число витков, приходящихся на единицу длины. Из /8/ имеем:

/9/

Индукция внутри бесконечно длинного соленоида равна числу ампер-витков на единицу длины. Вне бесконечно длинного соленоида магнитное поле отсутствует. В самом деле, если контур АВСД расположить вне контура, то охватываемый контуром ток равен нулю и:

Таким образом, в бесконечно длинном соленоиде магнитное поле однородно и полностью заключено внутри него.

Если внутреннее пространство бесконечного соленоида заполнить веществом с магнитной проницаемостью , то индукция магнитного поля возрастает в раз:

/10/

Если соленоид имеет конечные размеры, индукция магнитного поля внутри соленоида меньше:

/11/

где

/12/

Расстояния и отсчитываются от левого и правого конца соленоида /рис.2/.

Магнитное поле соленоида конечных размеров неоднородно /рис.3/. Области с наибольшей неоднородностью магнитного поля называют полюсами: северным , где линии магнитной индукции выходят из ка­тушки, и южным , где линии магнитной индукции входят в катушку. Степень неоднородности магнитного поля связана с расстоянием, т.е. величиной . В центре соленоида индукция магнитного поля максимальна. С перемещением к полюсам величина индукции магнитного поля уменьшается, что легко проверить, используя формулы /6/ и /7/. С увеличением длины соленоида при заданном его радиусе , величина индукции магнитного поля в центре соленоида приближается к величине индукции внутри бесконечно длинного соленоида.

Как следует из формул /4/ /6/, /7/ при длине соленоида в 10 раз превышающей радиус , индукция магнитного поля в центре соленоида на 2% меньше индукции магнитного поля бесконечного соленоида.

Для того, чтобы экспериментально изучить магнитное поле, созданное токами произвольной формы, необходимо измерить величину ин­дукции В в различных точках этого поля. Существует много методов измерения индукции магнитного поля.