
- •Типовой расчет по теме вычисление производной производная функции Пусть в некотором промежутке задана непрерывная функция . - заданная точка (рис.33).
- •Производную функции в произвольной точке х принято обозначать или , или . Если же точка задана, значение производной в этой точке записывают в виде , .
- •Основные правила дифференцирования
- •Дифференцирование функций, заданных параметрически
- •Контрольные варианты к задаче 2.
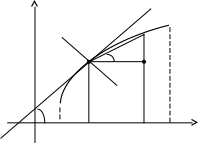
Типовой расчет по теме вычисление производной производная функции Пусть в некотором промежутке задана непрерывная функция . - заданная точка (рис.33).
Дадим
аргументу
Отношение
![]() приращение
приращение![]() ,
тогда функция получит прира-щение
,
тогда функция получит прира-щение
![]() ,
это величина отрезка ВС (рис.1).
,
это величина отрезка ВС (рис.1).
![]() называется средней
скоростью изменения фун-кции
в промежутке
называется средней
скоростью изменения фун-кции
в промежутке![]() ,
а предел этого
,
а предел этого
У Д
В
Е
![]()
А
![]()
С
![]()
О
а
![]() в х
в х
Рис. 1
отношения,
когда
![]() ,
называется производной
функции
в заданной точке
.
Таким образом,
,
называется производной
функции
в заданной точке
.
Таким образом,
![]() .
.
Замечание.
Если
![]() не
существует, то и производной
не
существует, то и производной
![]() тоже
не существует.
тоже
не существует.
Производную функции в произвольной точке х принято обозначать или , или . Если же точка задана, значение производной в этой точке записывают в виде , .
Производная
функции в заданной точке характеризует
скорость изменения функции в этой точке.
Например, производная от пути по времени
есть скорость движения, то есть
![]() ;
производная от скорости по времени дает
ускорение движения
;
производная от скорости по времени дает
ускорение движения
![]() .
Если функция
.
Если функция
![]() выражает количество электричества,
выражает количество электричества,
протекающего
за время t
через сечение проводника, то
![]() есть сила тока в момент времени t.
Видно (рис. 33), что
есть сила тока в момент времени t.
Видно (рис. 33), что
![]() .
Переходя к пределу при
,получаем
.
Переходя к пределу при
,получаем
![]() .
Итак, производная функции в заданной
точке равна тангенсу угла
,
который образует касательная в точке
.
Итак, производная функции в заданной
точке равна тангенсу угла
,
который образует касательная в точке
![]() с
осью ОХ:
с
осью ОХ:
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Поскольку уравнение прямой с угловым
коэффициентом имеет вид
.
Поскольку уравнение прямой с угловым
коэффициентом имеет вид
![]() ,
то получим уравнение касательной АД:
,
то получим уравнение касательной АД:
![]() (рис.
33).
(рис.
33).
Так
как нормаль
![]() , то
, то
![]() .
Поэтому уравнение нормали АЕ имеет вид
.
Поэтому уравнение нормали АЕ имеет вид
![]() (рис. 33).
(рис. 33).
Пример.
Найти производную функции
![]() в производной точке х.
в производной точке х.
Решение.
![]() ,
тогда
,
тогда
![]()
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
.
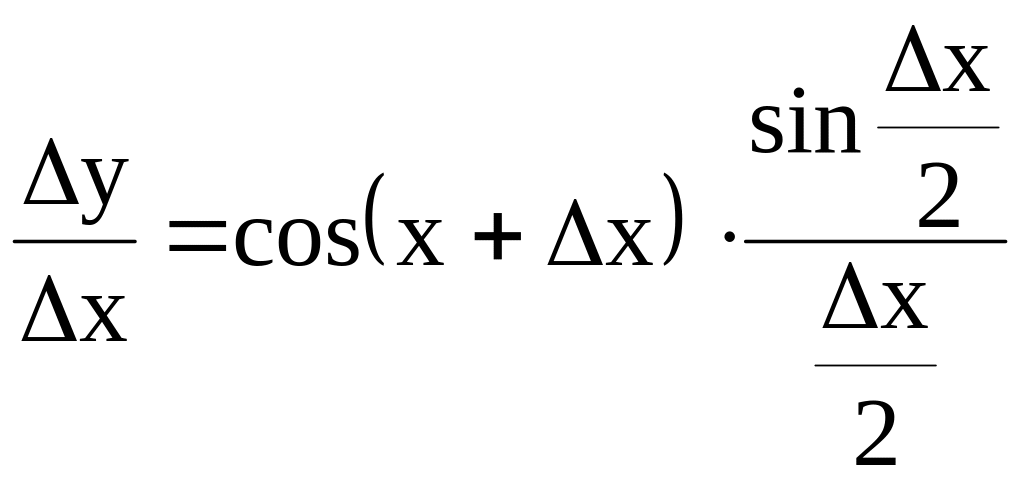 .
.
 .
.
Замечание.
При нахождении предела следует помнить,
что
![]() ,
,
![]() -переменная.
-переменная.
Основные правила дифференцирования
2) (U(x)V(x))=U(x)V(x)
3)(U(x)V(x))=U(x)V(x)+U(x)V(x)
4)![]() =
=![]()
5) (CU(x))=C(U(x))
C=0
x’=1
(xn)=nxn-1
(un)=nun-1u
(cosx)=-sinx
(cosu)=-sinu
u
(sinx)=cosx
(sinu)=cosu
u
(tgx)=
(tgu)=
(ctgx)=-
(ctgu)=-
(arctgx)=
(arctgu)=
(arcctgx)=-
(arcctgu)=-
u
(arcsinx)=
(arcsinu)=
(arccosx)=-
(arcosu)=-
u
(ax)=axlna
(au)=aulna
u
(ex)=ex
(eu)=euu
(logax)=
(logau)=
(lnx)=
(lnu)= |
Пример
2.
![]() .
.
Пример
3. Для
![]() найти
найти
![]()
Воспользуемся формулой :
(U(x)V(x))=U(x)V(x)+U(x)V(x),
где
![]() .Тогда
для
,
.Тогда
для
,
![]() .
.
Пример
4. Для
![]() найти
.
найти
.
Воспользуемся формулой :
=
,
где
![]() .
.
![]() Пример
5. Для
Пример
5. Для
![]() найти
.
найти
.
Это сложная функция. Можно представить
данную функцию как
![]() ,
где
,
где
![]() .
Зная, что
.
Зная, что
![]() ,
получим:
,
получим:
![]() .
.
Пример
6.
Для
![]() найти
.
найти
.
Это
сложная функция. Можно
представить данную функцию как
![]() ,
где
,
где
![]() .
Зная, что
.
Зная, что
![]() ,
получим:
,
получим:
![]() .
.
Пример
7. Для
![]() найти
.
найти
.
Это
сложная функция. Можно
представить данную функцию как
![]() ,
где
,
где
![]() .
Зная, что
.
Зная, что
![]() ,
получим:
,
получим:

Пример
8. Для
![]() найти
.
найти
.
Это
сложная функция. Можно
представить данную функцию как
![]() ,
где
,
где
![]() .
Зная, что
.
Зная, что
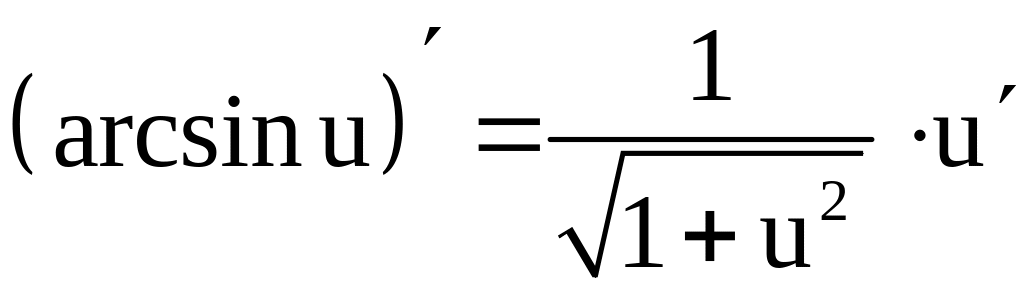 ,
получим:
,
получим:
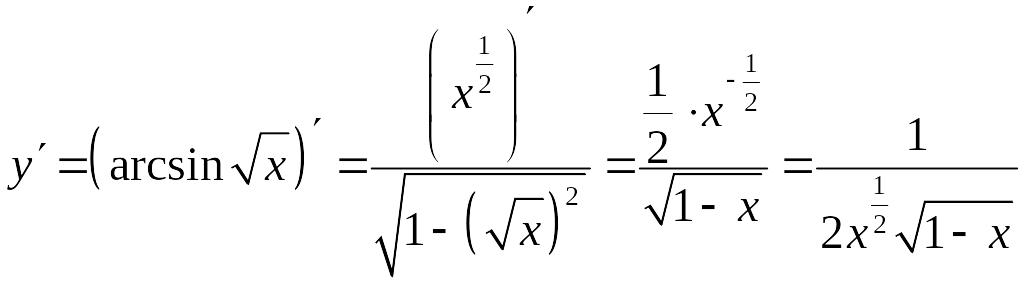
Задача 1. Найти производные функций:
1)
![]() .
.
![]() .
.
Можно представить данную функцию как
![]() ,
где
,
где
![]() .
Зная, что
.
Зная, что
![]() ,
получим
,
получим
![]()
Ответ:
![]() .
.
2)
![]() .
.
![]() .
.
Можно представить
![]() ,
где
,
где
![]() .
Причем
.
Причем
![]() ,
в результате получим
,
в результате получим
![]()
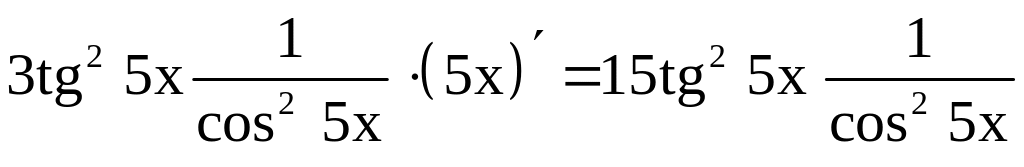
Ответ:
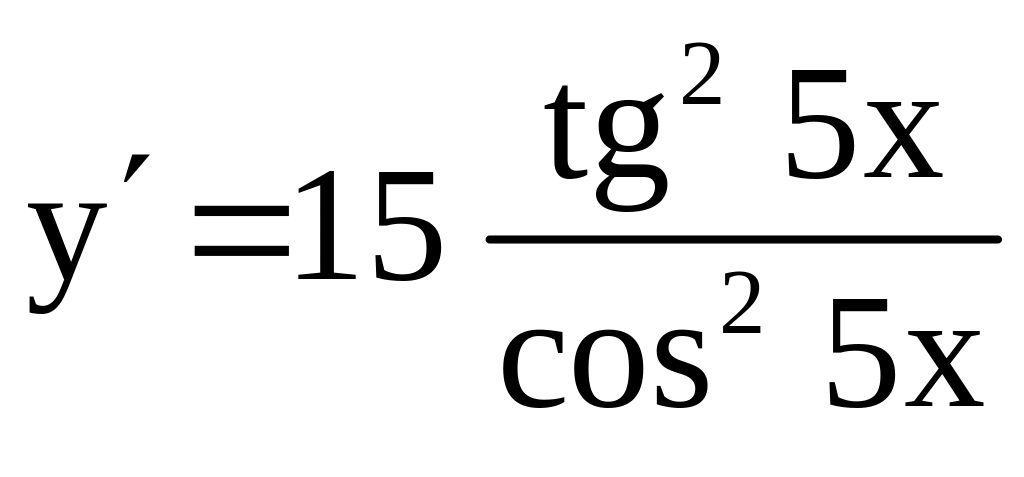 .
.
3)
![]() .
.
![]() .
.
После
подстановок
![]() получим
получим
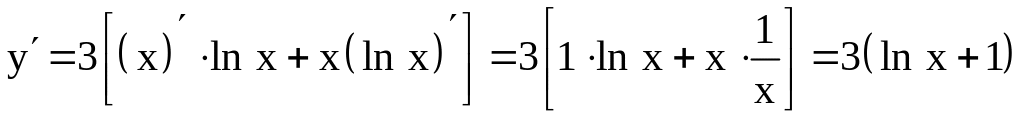 .
.
Ответ:
![]() .
.
4)
![]() .
.
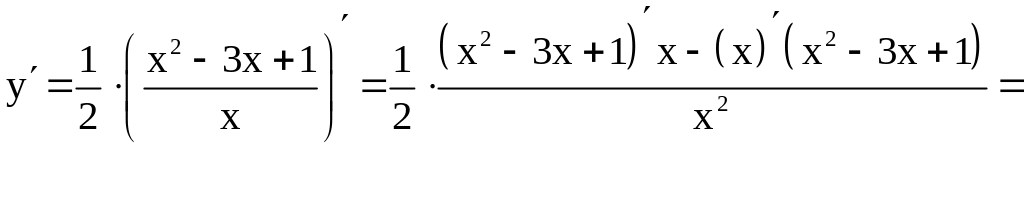
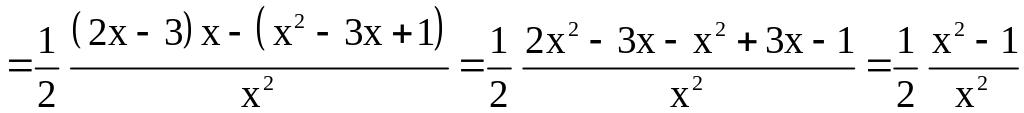 ,
если воспользоваться правилом
,
если воспользоваться правилом
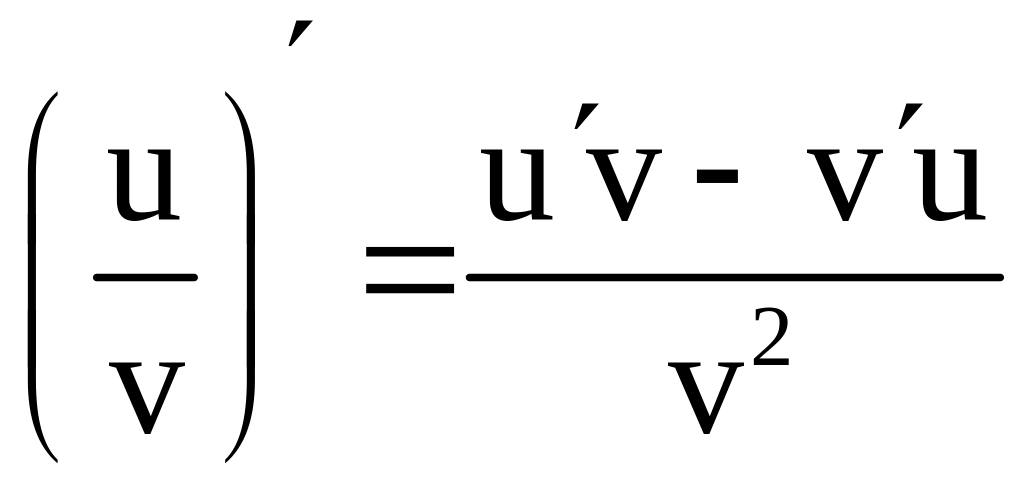 .
.
Ответ:
![]() .
.
Найти производные функций:
1. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
||
7)
|
8)
|
9)
|
||
10)
|
|
|||
|
||||
2. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
||
7)
|
8)
|
9)
|
||
10)
|
|
|||
3. |
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
|
10)
|
|
||
4. |
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
|
10)
|
|
||
5. |
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
|
10)
|
|
||
6. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
||
7)
|
8)
|
9)
|
||
10)
|
|
|||
7. |
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
||
7)
|
8)
|
9)
|
||
10)
|
|
|||
8. |
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
|
10)
|
|
||
9. |
1)
|
2)
|
3)
|
||||
4)
|
5)
|
6)
|
|||||
7)
|
8)
|
9)
|
|||||
10)
|
|
||||||
|
|||||||
10. |
1)
|
2)
|
3)
|
||||
4)
|
5)
|
6)
|
|||||
7)
|
8)
|
9)
|
|||||
10)
|
|
||||||
|
|||||||
11. |
1)
|
2)
|
3)
|
||||
4)
|
5)
|
6) ; |
|||||
7)
|
8)
|
9)
|
|||||
10)
|
|
||||||
12. |
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
|
10)
|
|
||
13. |
1)
|
2)
|
3)
|
||
4)
|
5)
|
6)
|
|||
7)
|
8)
|
9)
|
|||
10)
|
|
||||
|
|||||
14. |
1)
|
2)
|
3)
|
||
4)
|
5)
|
6)
|
|||
7)
|
8)
|
9)
|
|||
10)
|
|
||||
15. |
1)
|
2)
|
3)
|
||
4)
|
5)
|
6)
|
|||
7)
|
8)
|
9)
|
|||
10)
|
|
||||
16. |
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
|
10)
|
|
||
17. |
1) ; |
2) ; |
3) ; |
|
4) ; |
5) ; |
6) ; |
||
7) ; |
8) ; |
9) ; |
||
10) . |
|
|||
|
||||
18. |
1) ; |
2) ; |
3) ; |
|
4) ; |
5) ; |
6) ; |
||
7) ; |
8) ; |
9) ; |
||
10) . |
|
|||
19. |
1) ; |
2) ; |
3) ; |
4) ; |
5) ; |
6) ; |
|
7) ; |
8) ; |
9) ; |
|
10) . |
|
||
20. |
1) ; |
2) ; |
3) ; |
4) ; |
5) ; |
6) ; |
|
7) ; |
8) ; |
9) ; |
|
10) . |
|
||
21. |
1) ; |
2) ; |
3) ; |
4) ; |
5) ; |
6) ; |
|
7) ; |
8) ; |
9) ; |
|
10) . |
|
||
22. |
1) ; |
2) ; |
3) ; |
|
4) ; |
5) ; |
6) ; |
||
7) ; |
8) ; |
9) ; |
||
10) . |
|
|||
23. |
1) ; |
2) ; |
3) ; |
|
4) ; |
5) ; |
6) ; |
||
7) ; |
8) ; |
9) ; |
||
10) . |
|
|||
24. |
1) ; |
2) ; |
3) ; |
4) ; |
5) ; |
6) ; |
|
7) ; |
8) ; |
9) ; |
|
10) . |
|
||
25. |
1) ; |
2) ; |
3) ; |
||||
4) ; |
5) ; |
6) ; |
|||||
7) ; |
8) ; |
9) ; |
|||||
10) . |
|
||||||
|
|||||||
26. |
1) ; |
2) ; |
3) ; |
||||
4) ; |
5) ; |
6) ; |
|||||
7) ; |
8) ; |
9) ; |
|||||
10) . |
|
||||||
|
|||||||
27. |
1) ; |
2) ; |
3) ; |
||||
4) ; |
5) ; |
6) ; |
|||||
7) ; |
8) ; |
9) ; |
|||||
10) . |
|
||||||
28. |
1) ; |
2) ; |
3) ; |
4) ; |
5) ; |
6) ; |
|
7) ; |
8) ; |
9) ; |
|
10) . |
|
||
29. |
1) ; |
2) ; |
3) ; |
||
4) ; |
5) ; |
6) ; |
|||
7) ; |
8) ; |
9) ; |
|||
10) . |
|
||||
|
|||||
30. |
1) ; |
2) ; |
3) ; |
||
4) ; |
5) ; |
6) ; |
|||
7) ; |
8) ; |
9) ; |
|||
10) . |
|
||||
10) . |
|
||||

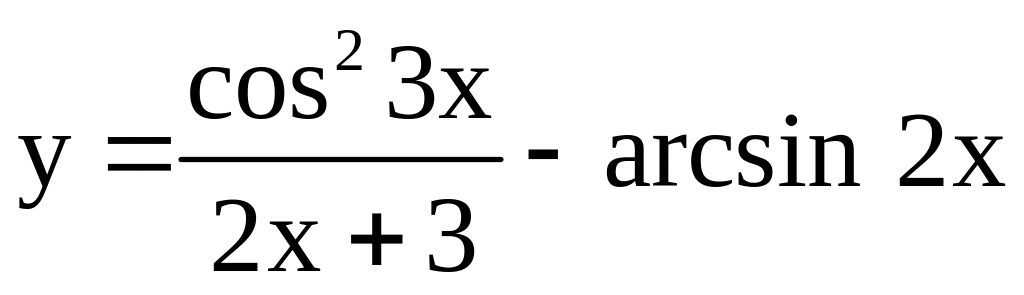 ;
;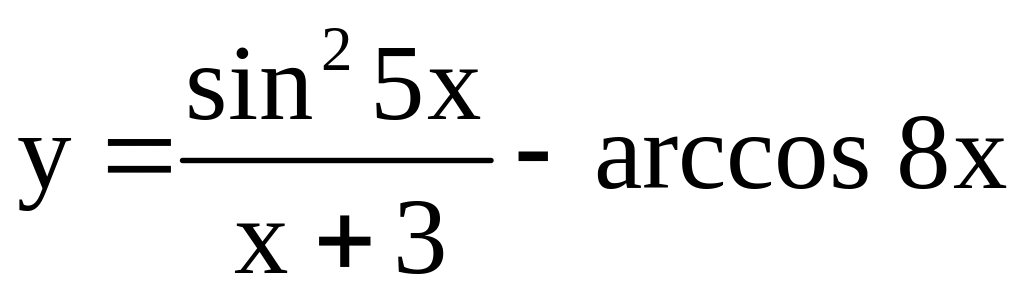 ;
; ;
;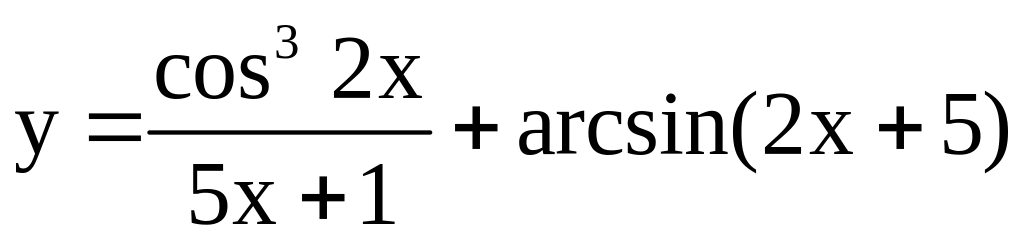 ;
;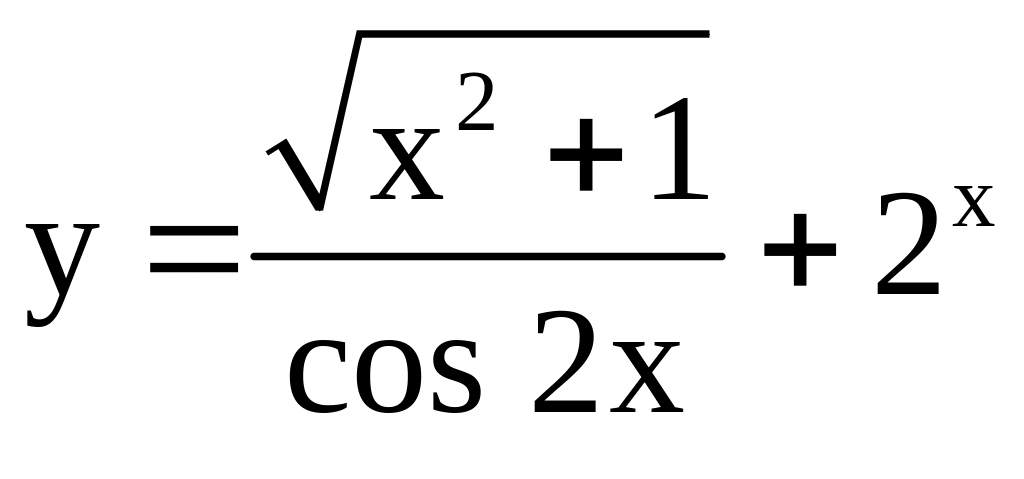 ;
;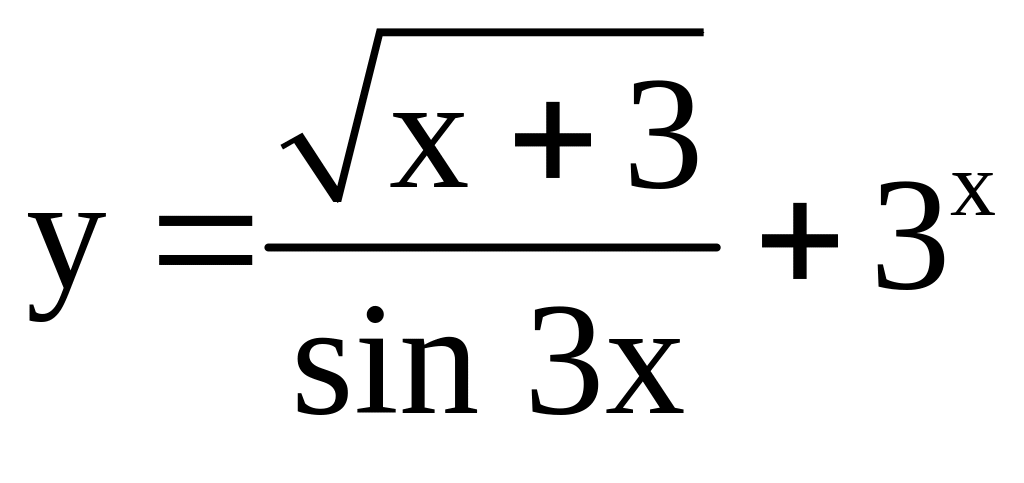 ;
;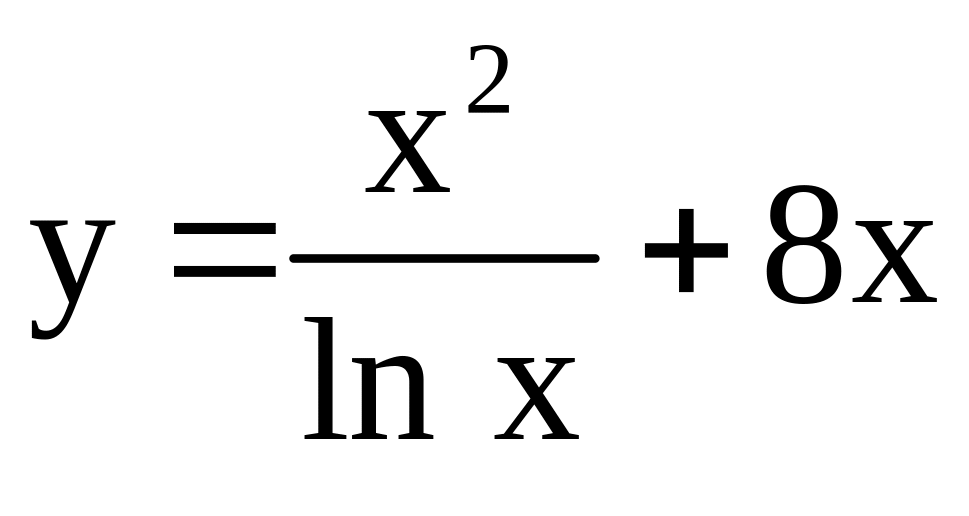 ;
;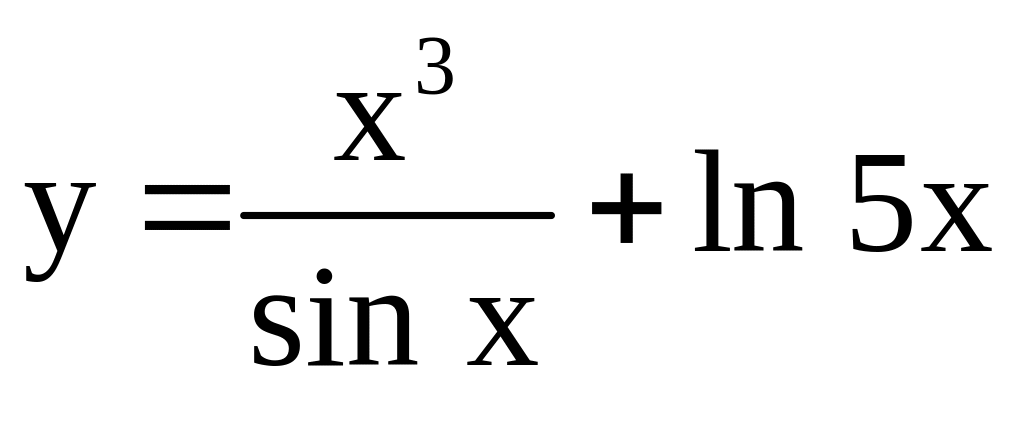 ;
;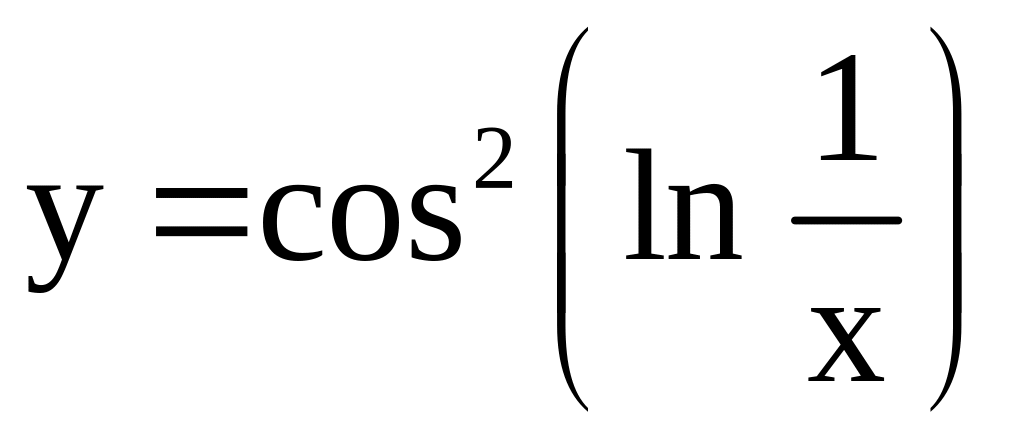 ;
;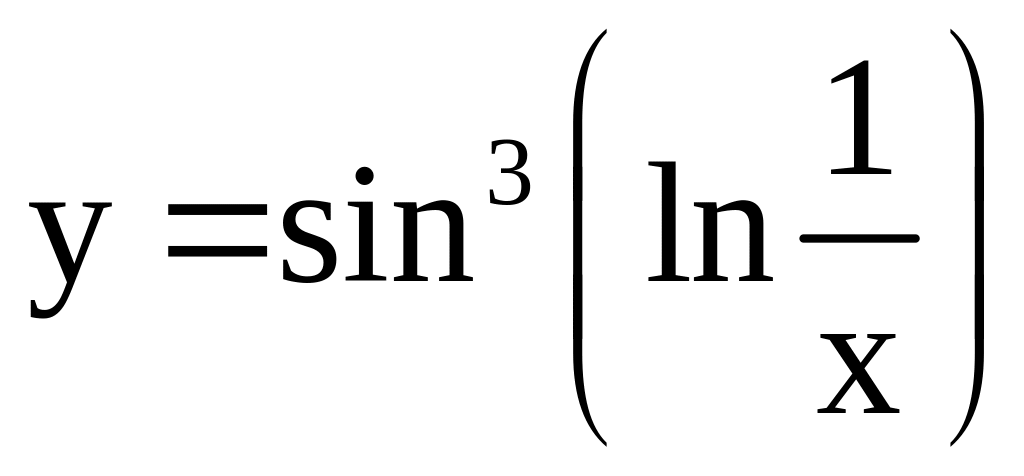 ;
;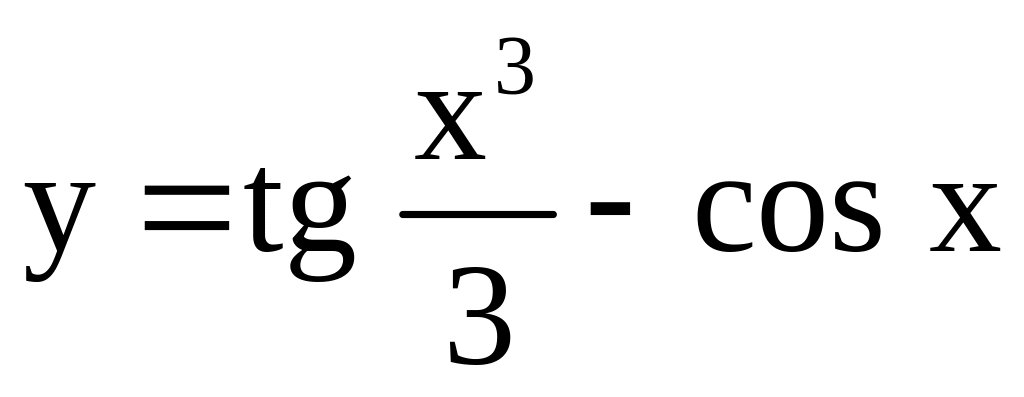 .
. ;
;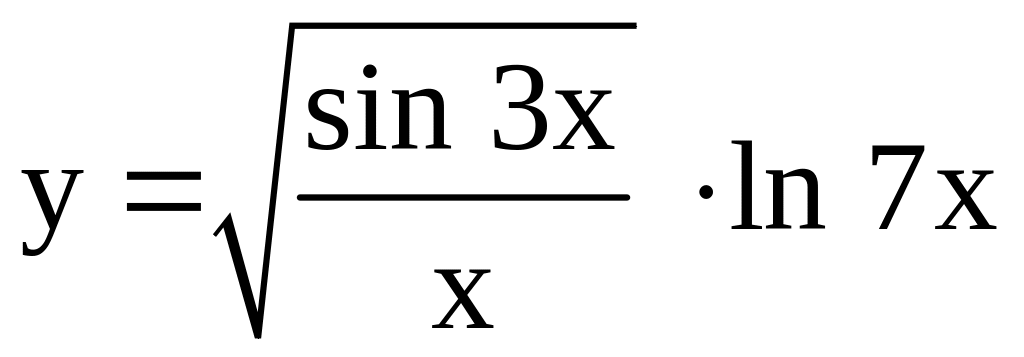 ;
;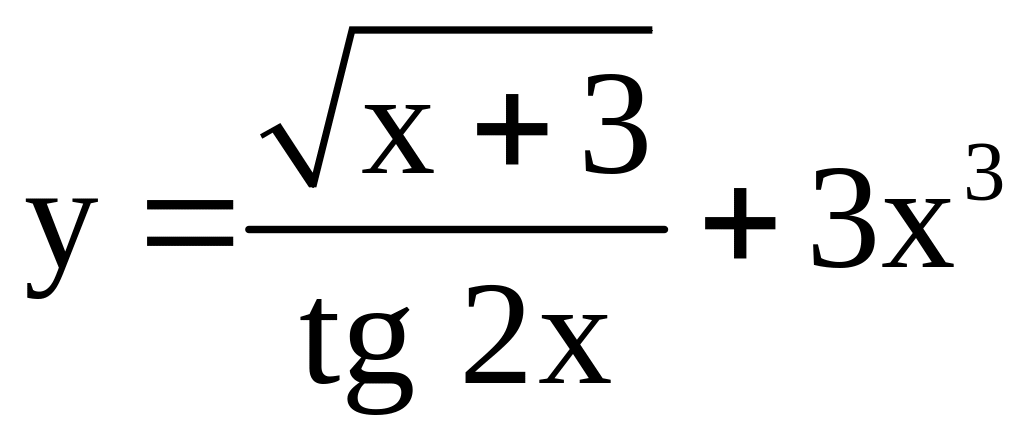 ;
; ;
;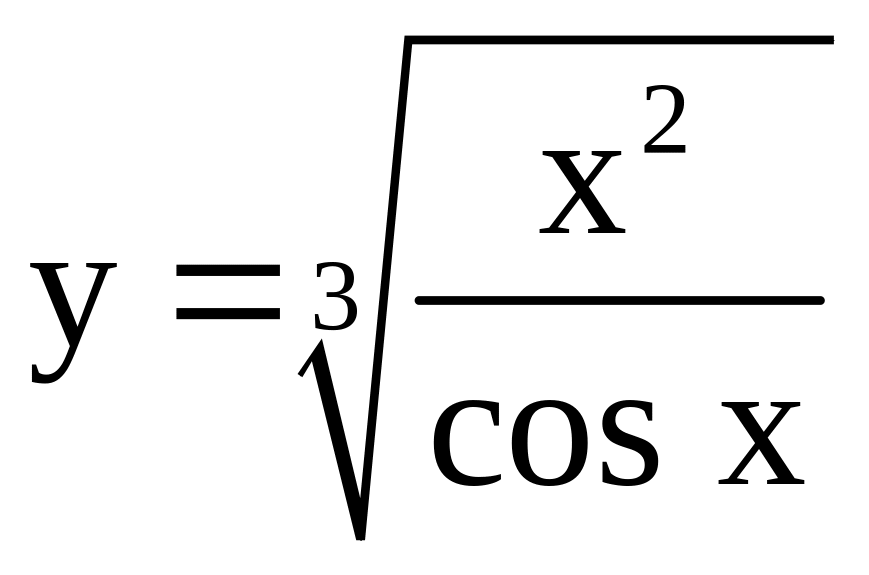 .
.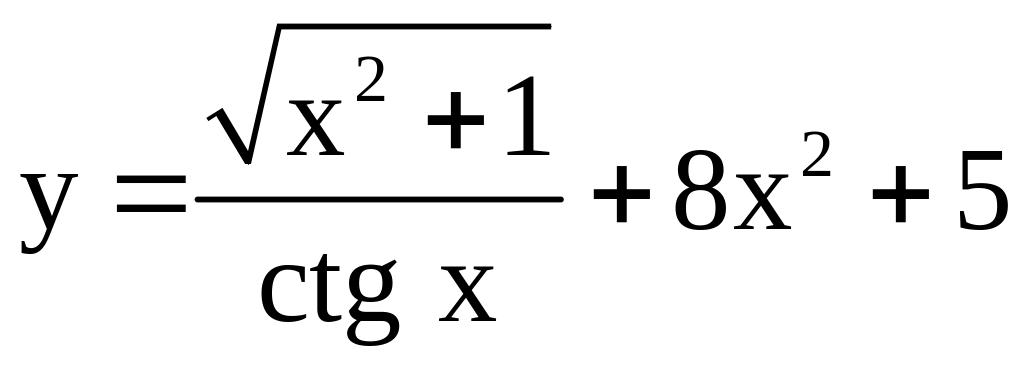 ;
; ;
;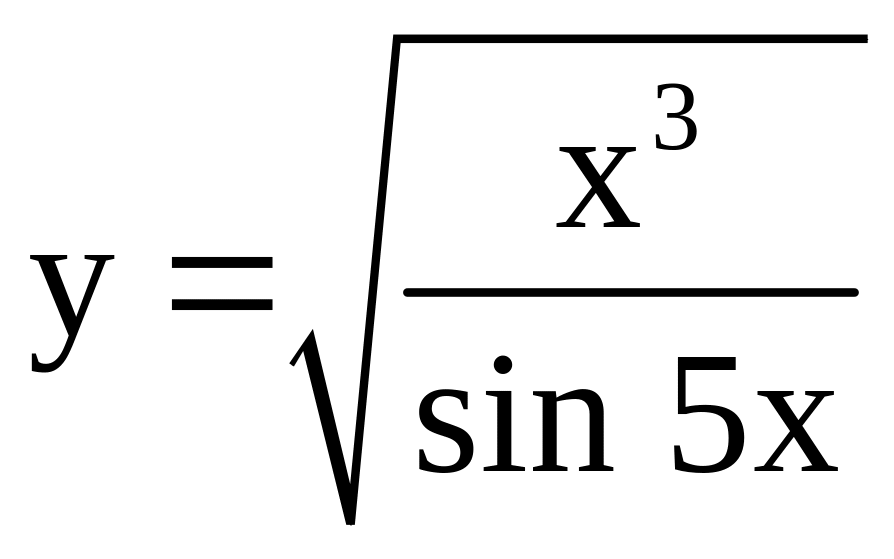 .
.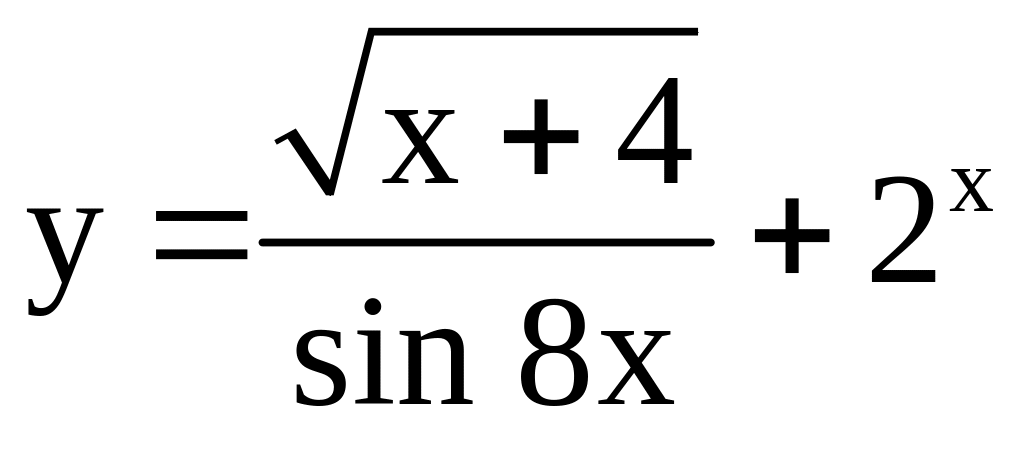 ;
;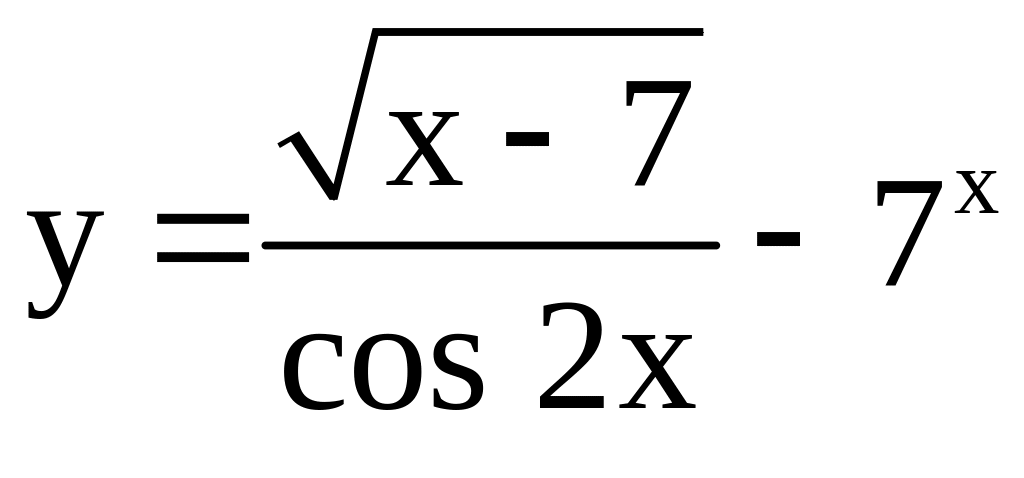 ;
;