
Гипотезы
Статистической гипотезой Н называется предположение относительно параметров или вида распределения случайной величины Х.
Проверяемая
гипотеза называется нулевой гипотезой
и обозначается
 .
Наряду с нулевой гипотезой рассматривают
одну из альтернативных (конкурирующих
гипотез)
.
Наряду с нулевой гипотезой рассматривают
одну из альтернативных (конкурирующих
гипотез)
 .
.
Правило,
по которому гипотеза принимается или
отклоняется, называется критерием κ,
для которого выбирается подходящая
статистика (статистика Z
критерия κ) . Уровень значимости
α определяет вероятность попадания
статистики критерия в область
 (критическую) при условии истинности
гипотезы
(
(критическую) при условии истинности
гипотезы
( ).
).
Проверка гипотезы, таким образом, разбивается на следующие этапы:
1)сформулировать проверяемую ( ) и альтернативную ( ) гипотезы;
2)назначить уровень значимости α;
3)выбрать статистику Z критерия для проверки гипотезы ;
4)определить выборочное распределение статистики Z при условии, что верна гипотеза ;
5)в зависимости от формулировки
альтернативной гипотезы определить
критическую область
одним из неравенств
 или
совокупностью неравенств
или
совокупностью неравенств
 ;
;
6)получить выборку наблюдений и вычислить
выборочное значение
 статистики критерия;
статистики критерия;
7)принять статистическое решение:
если
 ,
то отклонить гипотезу
как не согласующуюся с результатами
наблюдений;
,
то отклонить гипотезу
как не согласующуюся с результатами
наблюдений;если
 ,
то принять гипотезу
,
т.е. считать, что гипотеза
не противоречит результатам наблюдений.
,
то принять гипотезу
,
т.е. считать, что гипотеза
не противоречит результатам наблюдений.
Проверим гипотезу о равенстве дисперсий случайных величин X и Y.
1)проверяемая гипотеза
:
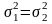 ,
,
альтернативная гипотеза
:
 ,
,
2)уровень значимости =0,05,
3)так как математические ожидания величин
неизвестны, но можно найти выборочные
средние, используем статистику Z= ,
,
4)выборочное распределение статистики
Z при условии, что гипотеза
верна, имеет вид
 ,
т.е. это распределение Фишера,
,
т.е. это распределение Фишера,
5)так как альтернативной гипотезой
выбрано выражение
,
областью принятия нулевой гипотезы
будет
 ,
,

6)выборочное значение
статистики критерия

7) 0,05<3,58, таким образом, значение статистики Z попадает в доверительную область, и, следовательно, на уровне доверия =0,95 (уровне значимости =0,05) можно считать, что результаты наблюдений не противоречат гипотезе , то есть гипотеза принимается.
Проверим гипотезу о равенстве математических ожиданий случайных величин X и Y.
1)проверяемая гипотеза
:
 ,
,
альтернативная
гипотеза
:
 ,
,
2)уровень значимости =0,05,
3)так как дисперсии величин неизвестны,
но можно найти их оценки
,
а так же при условии, что гипотеза
принимается, можно использовать
статистику Z= ,
где
,
где
 ,
,
4)выборочное распределение статистики
Z при условии, что гипотеза
верна, имеет вид
 ,
т.е. это распределение Стьюдента,
,
т.е. это распределение Стьюдента,
5)так как альтернативной гипотезой
выбрано выражение
,
областью принятия нулевой гипотезы
будет
 ,
,
 ,
,
6)выборочное
значение
статистики критерия


7)Таким образом, значение статистики Z попадает в доверительную область, и, следовательно, на уровне значимости =0,05 гипотеза также принимается.
