8. Оценки ширины фронта ударной волны.

Уравнением Бюргерса называют уравнение в частных производных, используемое в гидродинамике. Это уравнение известно в различных областях прикладной математики. Уравнение названо в честь Иоганна Мартинуса Бюргерса (1895—1981).

Пусть задана скорость течения жидкости u и ее кинематическая вязкость ν. Уравнение Бюргерса в общем виде записывается так:

.

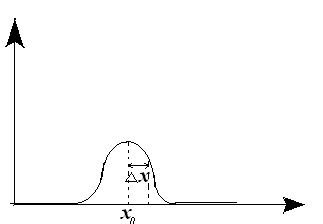
Процесс остановки опрокидывания волны и образования ударной волны определяется конкуренцией между нелинейностью и затуханием волны. Используя это, проведем оценку ширины фронта реальной

ударной волны.

Для этого запишем уравнение Бюргерса: , где - нелинейное слагаемое, - слагаемое связанное с затуханием.

Взаимоотношения нелинейности и затухания выражается с помощью числа Рейнольдса.

, для оценки этого числа заметим (1),

Где (1) пригодна для не слишком малых I. Если мы перейдем к приближению слабой диссипации, число Рейнольдса велико, т.е. R>>1. С помощью числа Рейнольдса оценим ширину фронта волны. Заметим, что Δx – область, где происходит сглаживание угла профиля. На этой длине Δx, конкуренция нелинейности и затухание, учитывая, что ,

9. Солитонные решения волнового уравнения(общие свойства).

Солито́н — структурно устойчивая, уединённая волна, распространяющаяся в нелинейной среде.

Солитоны ведут себя подобно частицам (частице подобная волна): при взаимодействии друг с другом или с некоторыми другими возмущениями они не разрушаются, а двигаются, сохраняя свою структуру неизменной. Это свойство может использоваться для передачи данных на большие расстояния без помех.

Основные свойства уравнения волны (солитонов) уравнение КДВ.

1. Амплитуда солитонов КДВ растет с ростом скорости, причем рост является линейным. А его длительность обратно пропорционально корню квадратному из скорости.

2. Знак решения в виде уединенной волны зависит от знака константы α.

3. Уединение волны уравнения КДВ однонаправлены, т.к. скорость не может быть отрицательной, т.к. должен быть действительными, а при k₁=k₂=0,

Более общее решение уравнения содержит и периодическую стационарную волну. Для получения этого решения следует взять нулевые значения постоянных k₁, k₂ и определенным образом подобрать положение нулей полинома Р.

Солитонное решение уравнения Кортевега - де -Вриза

Уравнение Кортевега-де-Вриза (КДВ) впервые появилось, когда изучались длинные волны на мелкой воде (каналы).

. (а)

. (б)

Слагаемые, пропорциональные , отражают нелинейность. А слагаемые, пропорциональные , связаны с дисперсией среды.

Уравнение КДВ описывает нелинейные волны в жидкостях (движение по трубам), распределение электромагнитных импульсов по нервным волокнам человека, гидродинамические волны в плазме, включая космическую плазму, и т.д.

Солитоном называют решение волнового уравнения в виде уединенной стационарной волны , которая при столкновении с другими такими же волнами асимптотически сохраняет свою форму и скорость.

Солитонные решения КДВ получили свое уравнение, исследуя распространение волн в одном направлении по поверхности мелкого канала.

- глубина канала (средняя величина);

, мало и определяет положение поверхности канала на дно (отклонение). Дифференциальное уравнение в частных производных, описывающее движение волны:

. (1)

- гравитационная постоянная.

- произвольная постоянная;

- плотность жидкости;

- поверхностное натяжение жидкости.

Сделаем замену переменных: , , (2).

. (3)

. (4)

Будем искать решение в виде стационарной волны , . (5)

- скорость бегущей волны.

Сделаем замену: , , . (6) Подставим (6) в (4):

. (4’)

. (5) .

, (6) .

. (7)

.

. (8)

. (9)

. (10)

.

(11) - эллиптический интеграл.

Т.к. уединенная волна локализована в некоторой области, то ее первая и вторая производные при будут равны нулю.

Из уравнений (7), (9) для солитонного решения.

Полином (10) сильно упрощается и интеграл можно взять. Тогда решение будет:

(12) – решение в виде солитона.

Основные свойства солитонов уравнения КДВ

1. Амплитуда солитонов КДВ растет с ростом скорости (линейно). А его длительность обратно пропорциональна квадратному корню из скорости.

2. Знак решения в виде уединенной волны зависит от знака .

3. Уединенные волны уравнения КДВ однонаправлены, т.к. скорость не может быть отрицательной, т.к. должно быть действительным, а при .

Более общее решение уравнения (11) содержит и периодическую стационарную волну. Для получения этого решения следует взять ненулевые значения постоянных и определенным образом подобрать положение нулей .