6. Преобразование Коула –Хопфа.

Пусть имеется уравнение Бюргерса

, - (1)

- (2), где - произвольное число.

Данная замена определяет функцию F с точностью до времени.

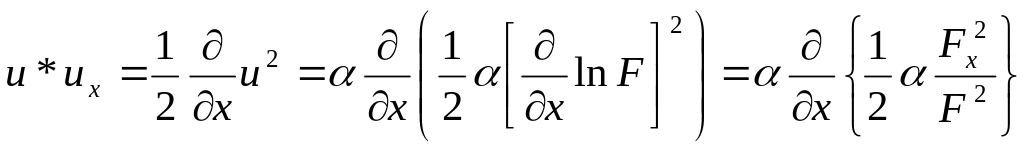
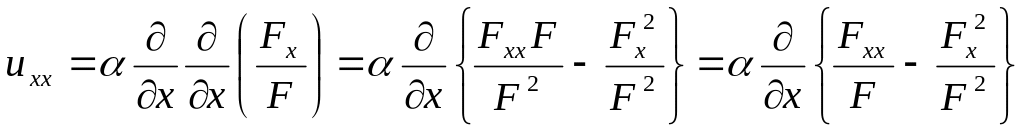
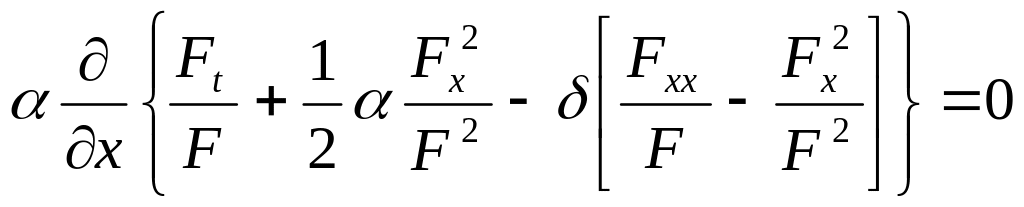
Определимся с постоянной .

- (3)

, т к F(x, t) определяется с точностью до функции времени, то c(t) включается в F(x, t) и правая часть равна нулю.

Т к , то можно записать:

- (4) – уравнение теплопроводности.

Н у: - (5)

- (6)

y – то же, что и x, но по источнику.

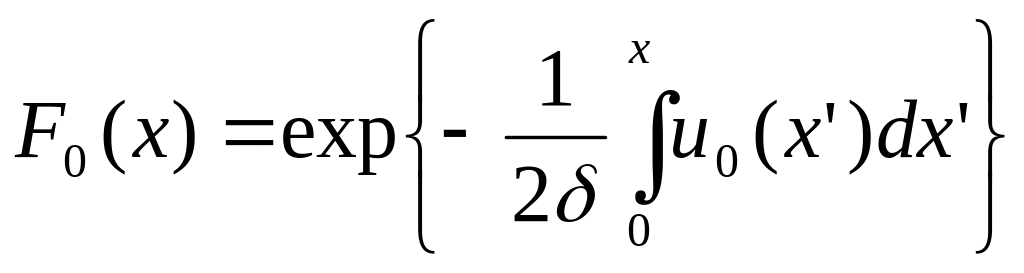- (7)

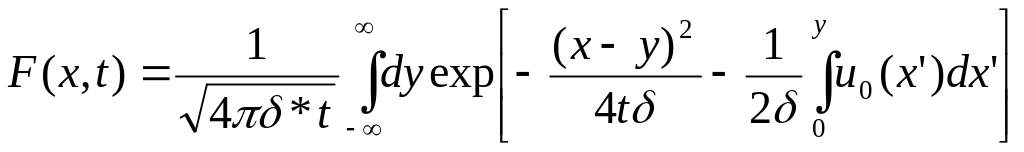
Введем функцию - (8)

- (9)

Подставляем в (2) и получим уравнение Бюргерса

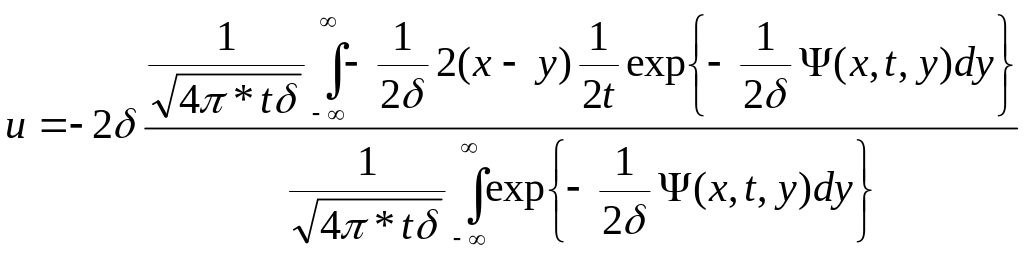
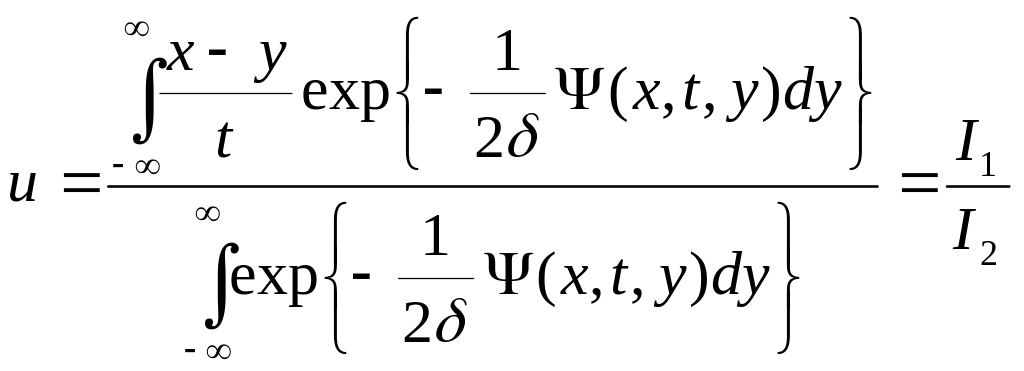(10)

Решение (10) позволяет получить произвольные решения для уравнения Бюргерса, соответствующие различным начальным профилям волны.

Однако чтобы получить решение, необходимо пользоваться вычислительными методами в общем случае.

7. Асимптотические решения уравнения Бюргерса.

Уравнением Бюргерса называют уравнение в частных производных, используемое в гидродинамике. Это уравнение известно в различных областях прикладной математики. Уравнение названо в честь Иоганна Мартинуса Бюргерса (1895—1981).

Запишем уравнение Бюргерса : .

Проинтегрируем данное уравнение в пределах от .

(*)

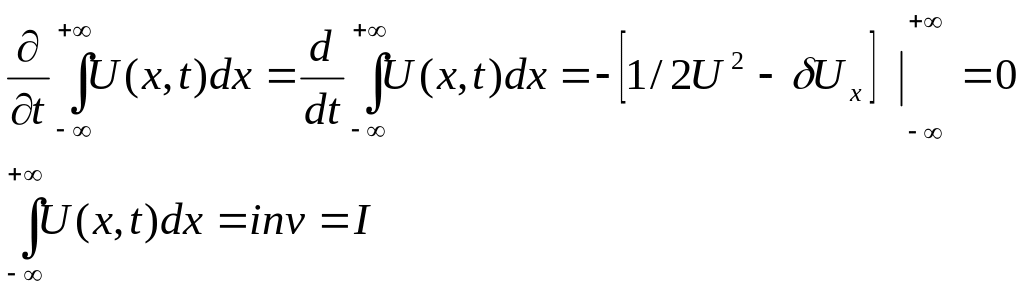I- определяет асимптотическую форму импульса (профиль решения) следующего уравнения: (**)

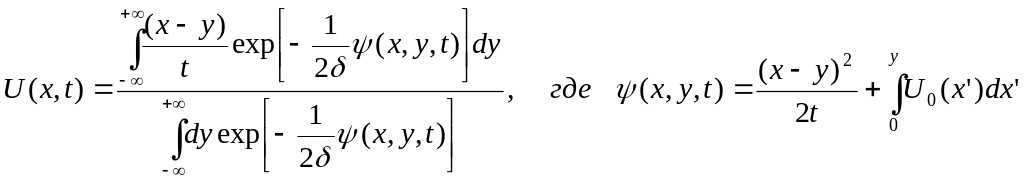Рассмотрим случай для малых δ. При малых δ выход волны на стационарный режим будет происходить при достаточно больших t, это следует из структуры уравнения Бюргерса, где t входит в [δt]. При малых δ интегралы уравнений (**) можно вычислить методом наискорейшего спуска.

Данная стационарная точка удовлетворяет уравнению:

(***)- уравнение, удовлетворяющее стационарной точке, тогда

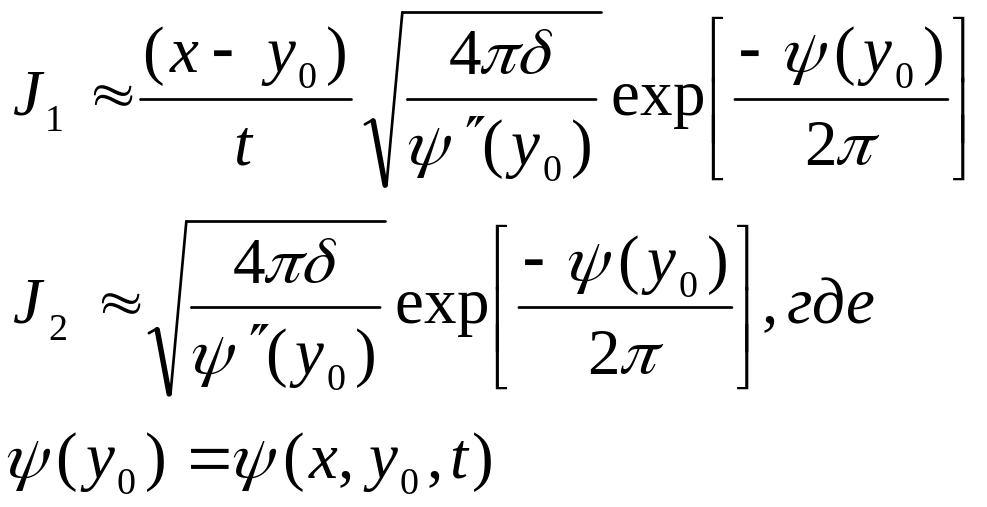
(****) - асимптотическое решение. При больших t, которые стремятся к бесконечности, отличные от нуля значения волны получаются при достаточно больших х, поэтому практически во всей области, где профиль U(x,t) принимает ненулевые значения, имеет место асимптотическая форма решения, где х и t связаны соотношением (***), т.е. , значит, мы получили в асимптотике обычную стационарную волну с линейным профилем.

Нелинейная волна с линейным профилем подвержена явлению укручения фронта волны. Вязкость (затухание волны) среды приводит к ослаблению данного эффекта. С другой стороны, если подставить (****) в инвариант (*) это означает, что решение справедливо только для некоторого значения x=x₀ достаточно большого, т.е. при x>x₀ >>y₀, тогда U(x) 0, чтобы найти x₀ воспользуемся инвариантом (*), из инварианты следует, что . При этом мы учитываем, что на нижнем пределе , при x<0. .

(‘)

Таким образом, и (‘) показывают, что асимптотический профиль определяется только значением инварианты U при J > 0 не зависит от начального профиля волны U₀(x).

Полученное решение уранения Бюргерса, в которых не происходит явление опрокидывания волны, является примером образования ударной волны. В ударной волне могут существовать скачки плотности среды и скорости волны нормальной к фронту волны, что следует из полученного решения.