4. Нелинейные волновые уравнения.

Рассмотрим основные типы нелинейных волновых уравнений.

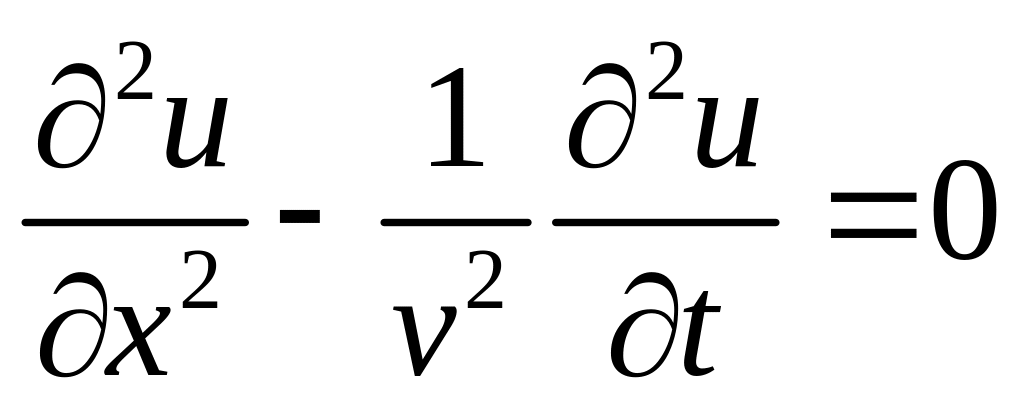
Для данного уравнения существует два общих решения, представляющих бегущую волну вправо и бегущую волну влево.

.

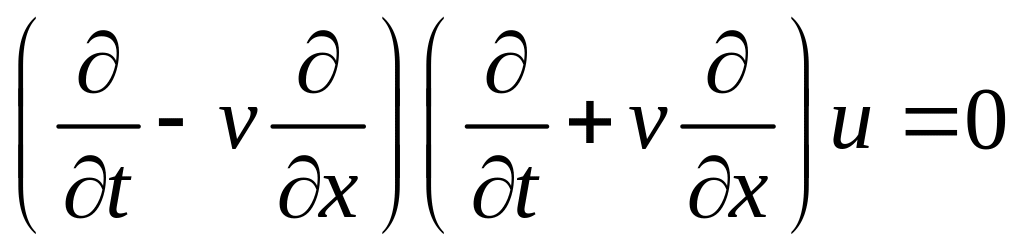
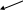Общее решение этого уравнения: . Уравнение описывает паводковые волны, волны химических реакций, в ледниках и т.д.

Перейдем к нелинейным задачам:

пусть скорость зависит от u, тогда

, где v-скорость распространения волны есть функция локального возмущения.

Исследование этого уравнения дает все понятия нелинейных гиперболических волн.

Уравнение относится к классу уравнений первого порядка квазилинейных уравнений. Оно квазилинейно, т.к. нелинейно относительно u и линейно относительно производной.

Одним из простейших модельных уравнений, описывающее нелинейные волны в средах с дисперсией является уравнение Картевега-де-Вриза (КВД).

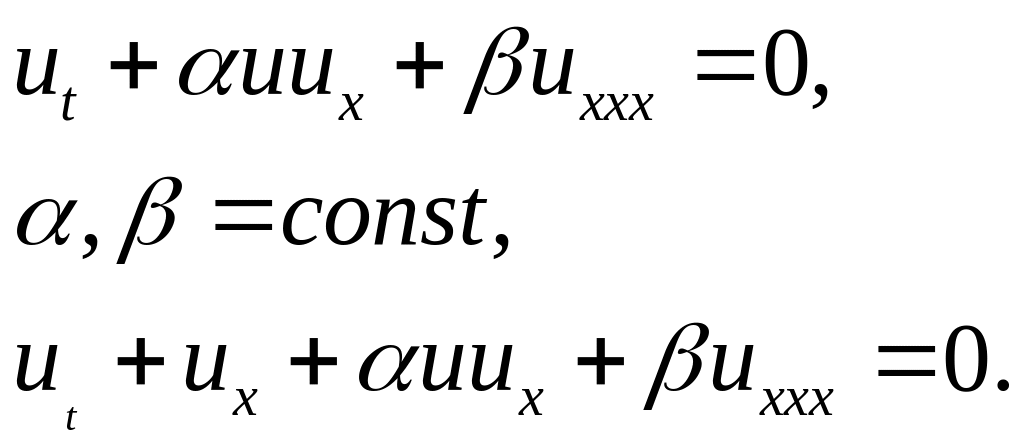
Слагаемое отражает явление нелинейности, а --связано с дисперсией среды.

Уравнение КДВ описывает нелинейные уравнения движения жидкости по трубам, распространение электромагнитного импульса по нервным волокнам человека, гидродинамические волны в плазме.

Другой тип уравнений, описывающий нелинейные волны—уравнение Бюргерса.

Правая часть определяет затухание волн в среде.

Это уравнение применяется для описания турбулентного движения жидкости в трубе, описывает нелинейность электромагнитных волн (лазерных лучей в атмосфере, а именно самофокусировку).

5. Явление опрокидывания нелинейных волн

Рассмотрим уравнение Кортевега-де-Вриза (КВД):

.

Чтобы выделить явление нелинейности, будем пренебрегать дисперсией среды, т.е. отбросим .

Начальное возмущение: . (*)

Уравнение перепишется: , (1)

Решение уравнения (1) запишется в виде: (2)

Выражение (2) можно рассматривать как функциональное уравнение, эквивалентное уравнению (1).

П роверим: , где - производная по аргументу, .

(3)

=>

Для наглядности рассмотрим эволюцию начального треугольного импульса.

Н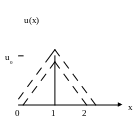 .у. импульса:

Кусочно-линейная функция, описывающая начальное возмущение в форме треугольника.

Эта форма начального импульса является достаточно хорошим приближением реального импульса более общей горбовидной формы.

Используем функциональное уравнение (2):

Введем новую переменную , , тогда:

В остальных случаях.

На основе функционального уравнения (2):

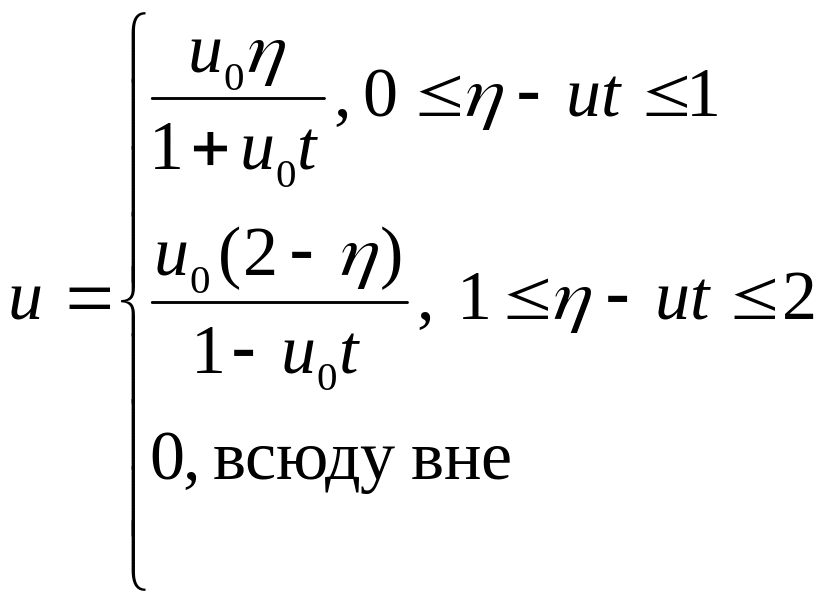
Возьмем производную:

u₀

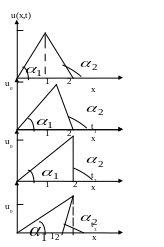
Импульс меняет формы

в точке , импульс имеет прямоугольную форму.

При производная правой стороны импульса становится положительной, импульс принимает форму при t_3.

В промежутке [x₁; 2] появляется неоднозначность функции.

Если волновой процесс (например, описывает колебание плотности среды), то в данной точке пространства значение u будет разным (2 значения), а т.к. u описывает при этом плотность вещества, то в заданной точке пространства мы будем иметь разную плотность вещества.

Этот результата получается из-за того, что при t = t_кр происходит разрушение волны.

Обратимся к соотношениям (3).

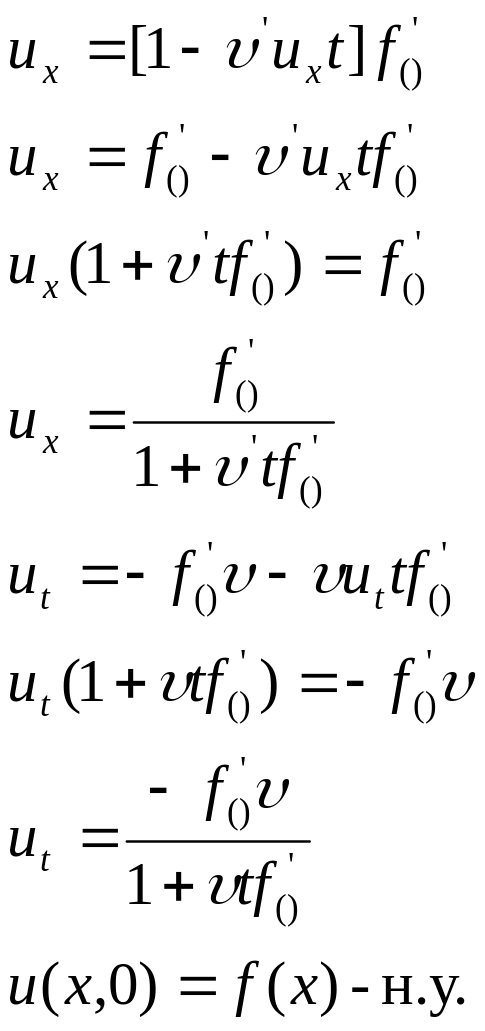
Если , то исходная функция однородная, то она будет константой и дальше.

означает неоднородность начального профиля волны (согласно (*)).

, то скорость зависит от u. => волна нелинейная.

t_кр определяет время разрушения волны:

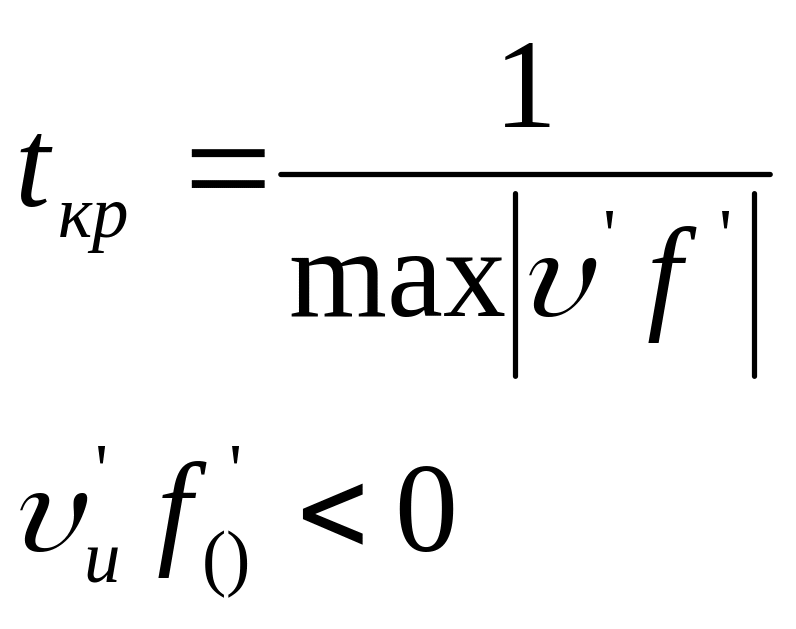укручение волны.

Для волны сжатия : t_кр существует только в том случае, если .

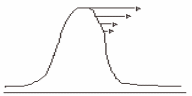
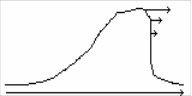
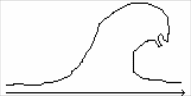
t₀ x t₁ x t₂ x

Замечания:

В действительности, опрокидывание волны, подобное тому, что возникает на поверхности волны при сильном разгоне, наблюдается далеко не всегда. Процесс опрокидывания волны приостанавливается, если среда, в которой распространяется волна, обладает диссипацией или дисперсией.

Диссипация и дисперсия являются конкурирующими процессами с нелинейностью.

В результате этой конкуренции опрокидывание волны не происходит, и устанавливаются ударные волны.