1. Характеристики линейных волн.

Реальная волна имеет следующие характеристики:

• Амплитуда А, для линейной волны это const

• Фаза волны , для одномерной волны ,

где k – волновой вектор

- частота волны

- начальная фаза

Фаза не имеет глубокого смысла. Имеет смысл разность фаз.

Волна в общем случае будет записываться в следующем виде: .

Физический смысл имеет реальная часть: .

В общем случае - это вектор.

Если , то это поперечная волна (например, электромагнитная волна ).

Если , то это продольная волна (волны пространственного заряда, распространенные волны в веществе).

Волны, у которых на плоскости могут быть цилиндрическими.

Точечный источник имеет сферическую волну.

Для линейных волн фаза является линейной функцией времени и координат.

2. Фазовая и групповая скорости линейных волн

Фазовая скорость определяется как скорость движения постоянной фазы.

Фаза будет постоянной для наблюдателя, который двигается со скоростью , которая обеспечивает .

Фазовая скорость имеет направление распространения волны.

Если среда с дисперсией, то фазовая скорость - функция волнового вектора

Фазовая скорость не переносит энергию, поэтому она может превышать , такие волны называют быстрыми волнами. Обычно в реальных условиях происходит, что фазовая скорость волны зависит от волнового вектора. кроме того, даже самый монохроматический волновой источник дает нам конечный во времени импульс

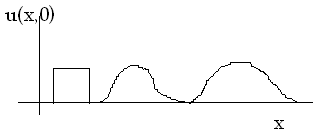
Поскольку , то это обозначает, что каждая волна, которая заполняет этот импульс, будет двигаться со своей скоростью, это приведет к изменению формы импульса, т.е. фазы волн, которые заполняют эти импульсы, будут меняться, и форма импульса может измениться. Отсюда следует, что, если среда диспергирующая, то фазовая скорость волны может сильно отличаться от скорости переноса энергии импульса. Для диспергирующей среды можем считать, что частота .

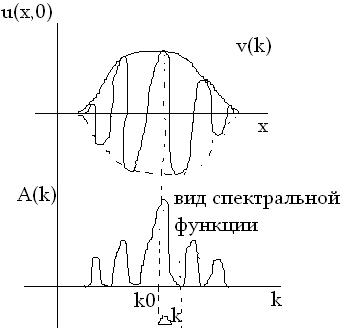
Учитывая, что - небольшое, можем представить частоту:

Импульс во времени

Огибающая несет энергию

Максимум, огибающей из уравнения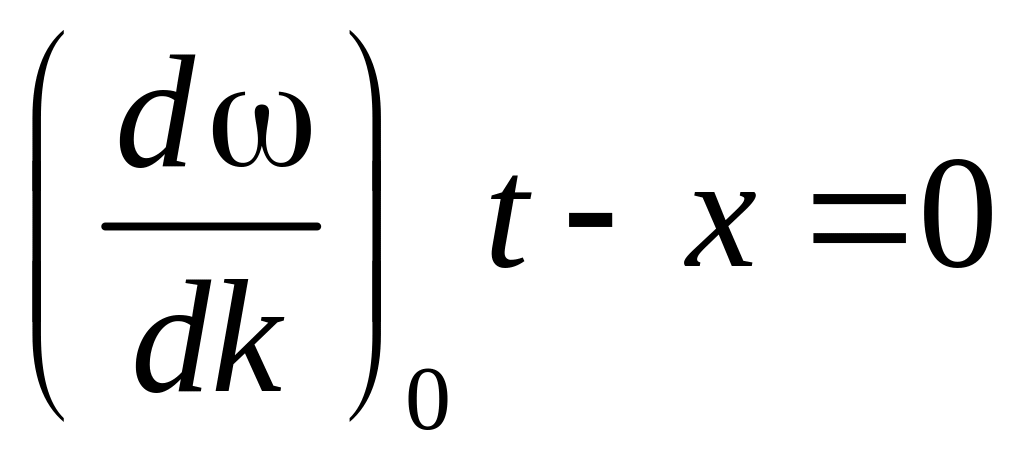

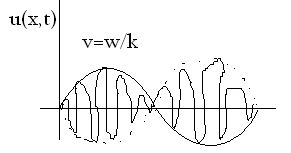
3. Решение в виде бегущих волн линейного волнового уравнения

Пусть U – некоторый n-мерный вектор, описывающий некоторый волновой процесс и являющийся функцией координаты и времени. Тогда его эволюцию описывает волновое уравнение Даламбера:

(1)

- n-мерный оператор Лапласа по координатам (p), F(p,t) – правая часть, зависящая от координаты и времени, - действующая внешняя сила, >0 – имеет смысл скорости; начальные условия:

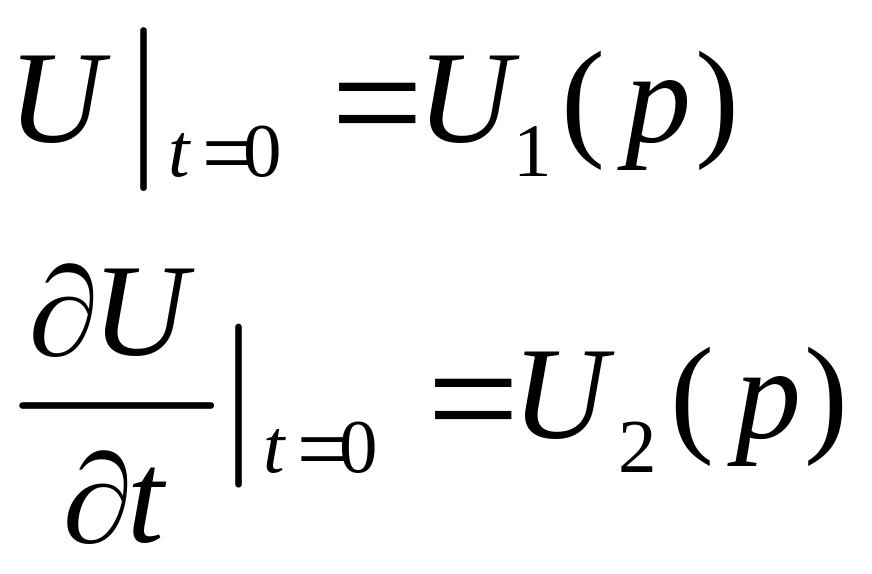(2)

Если = const (не зависит от U), то уравнение линейное.

Рассмотрим одномерное уравнение U(x,t) = 0, т.е.

. (3)

Можно привести примеры волновых процессов, описываемых данным уравнением:

• колебания бесконечной струны, тогда: U(x,t) – отклонение от положения равновесия, - скорость распространения сигнала по струне ( , - натяжение струны, - линейная плотность),

• Электромагнитные колебания, .

Введем новые переменные:

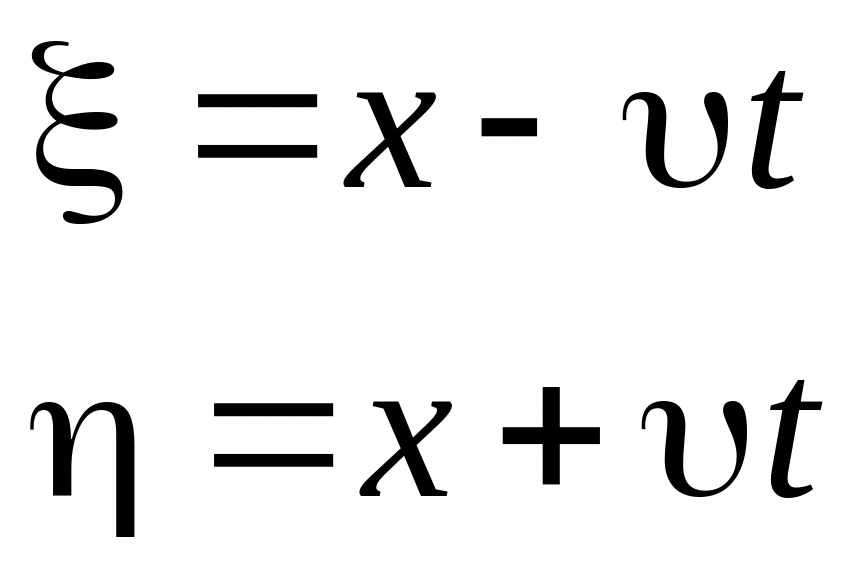, тогда решением уравнения (3) будет любая дважды дифференцируемая функция от ( , ):

, (4)

где - описывает расходящуюся волну от источника (расходящаяся волна), - описывает волну, приходящую в некоторую область (сходящаяся волна).

Решение (4) называется решением в виде бегущих волн.

Для линейных волн удобно использовать преобразование Фурье:

, где (5)

k - волновой вектор, - частота колебаний. В общем случае волновой вектор и частота связаны между собой. Можно записать дисперсионное уравнение:

(6)

Это уравнение, как правило, вытекает из граничных условий задачи. В самом простом случае частота и характеристики среды не зависят от k, то есть, нет дисперсии среды. Если рассматривать ЭМ волну в неограниченном пространстве, то уравнение (6) преобразуется к следующему соотношению:

. (7)

В (5) A(k) – амплитуда с волновым числом k, описывает свойства суперпозиции различных волн. Амплитуда A(k) определяется через значение величины U(x,t) в начальный момент времени: - известно

. (8)

Пусть начальное возмущение среды передается в виде гармонической волны.

,

.

,при