Спираль Архимеда

Одна из ветвей спирали Архимеда, задаваемая уравнением для .

Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:

r(φ) = a + bφ.

Изменения параметра a приводят к повороту спирали, а параметра b — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для φ > 0 а другую для φ < 0. Две ветви плавно соединяются в полюсе. Зеркальное отображение одной ветви относительно прямой, проходящей через угол 90°/270°, даст другую ветвь. Эта кривая интересна тем, что была описана в математической литературе одной из первых, после конического сечения, и лучше других определяется именно полярным уравнением.

[править] Конические сечения

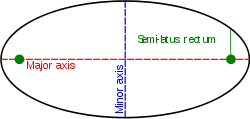
Эллипс.

Коническое сечение, один из полюсов которого находится в полюсе, а другой где-то на полярной оси (так, что малая полуось лежит вдоль полярной оси) задаётся уравнением:

где e — эксцентриситет, а — фокальный параметр. Если e > 1, это уравнение определяет гиперболу; если e = 1, то параболу; если e < 1, то эллипс. Отдельным случаем является e = 0, определяющее окружность с радиусом .

Комплексные числа

Пример комплексного числа , нанесённого на комплексную плоскость.

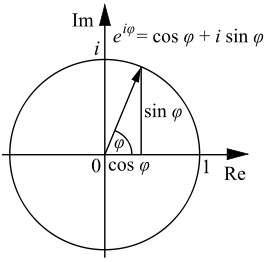
Пример комплексного числа, нанесённого на график, с использованием формулы Эйлера.

Каждое комплексное число может быть представлено точкой на комплексной плоскости, и, соответственно, эта точка может определяться в декартовых координатах (прямоугольная или декартова форма), либо в полярных координатах (полярная форма). Комплексное число z может быть записано в прямоугольной форме так:

z = x + iy,

где i — мнимая единица, или в полярной (см. формулы преобразования между системами координат выше):

и отсюда:

z = re^iφ,

где e — число Эйлера. Благодаря формуле Эйлера, оба представления эквивалентны^[16] (Следует отметить, что в этой формуле, подобно остальным формулам, содержащим возведения в степень углов, угол задан в радианах)

Для перехода между прямоугольным и полярным представлением комплексных чисел, могут использоваться указанные выше формулы преобразования между системами координат.

Операции умножения, деления и возведения в степень с комплексными числами, как правило, проще проводить в полярной форме. Согласно правилам возведения в степень:

• Умножение:

• Деление:

• Возведение в степень (формула Муавра):

(re^iφ)ⁿ = rⁿe^inφ.

Векторный анализ

Для полярных координат можно применить элементы векторного анализа. Любое векторное поле можно записать в полярной системе координат, используя единичные векторы:

в направлении , и

Связь между декартовыми компонентами поля F_x и F_y и его компонентами в полярной системе координат задаётся уравнениями:

F_x = F_rcos φ − F_φsin φ;

F_y = F_rsin φ + F_φcos φ.